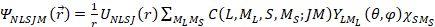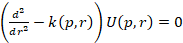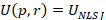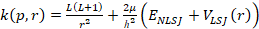Superheavy nuclei and their associated stability continue to be active experimental and theoretical areas of research. Calculations in the superheavy mass region require the selection of an appropriate nuclear interaction. Although this interaction is usually based on the extrapolation of a known nuclear interaction, any approach becomes more uncertain as calculations proceed beyond mass regions that have been explored experimentally. In view of these uncertainties, calculations can only provide qualitative results. These extrapolations and the associated model results become more uncertain as the system mass increases.
Previous calculations explored the 570 ≤ A < 1630 mass region. This paper extends these calculations into the 1630 ≤ A < 1640 region. The single-particle level spectrum is generated using a Woods-Saxon potential with parameters optimized to permit extrapolation into the A ≥ 1600 superheavy region utilizing the Rost-1600 interaction that was based on existing nuclear systems as well as nuclear matter calculations. This interaction is essentially the Rost interaction that includes a 15% uncertainty in the potential strength. Calculated single-particle energies are also derived by incorporating the unmodified pairing interaction of Blomqvist and Wahlborn to investigate the bounding characteristics of A ≥ 1600 superheavy nuclear systems.
The stability of 1630 ≤ A < 1640 systems is determined by evaluating the various decay modes (i.e., alpha decay, beta decay, positron decay, electron capture, and spontaneous fission). Based on previous calculations, stability in the 1630 ≤ A < 1640 mass region is expected to be dominated by alpha decay and beta decay.
Given uncertainties in the model interaction, it is not practical to determine absolute values for the half-lives and Q-values. However, the model does permit establishing the relative stability of nuclear systems and to highlight possible islands of stability. Using the Rost-1600 interaction, 47 even-even nuclear systems are predicted in the 1630 ≤ A < 1640 mass region. For this mass region, the model predicts a new island of stability in the vicinity of the Z = 442 – 448. Model calculations suggest that the most stable 1630 ≤ A < 1640 system occurs at (Z, A) = (442, 1638).
1630 ≤ A < 1640 Superheavy Nuclei; Alpha Decay; Spontaneous Fission; Beta Decay; Positron Decay; Electron Capture
Superheavy nuclei and their associated stability have been active experimental and theoretical areas of research [1-37]. Calculations in the superheavy mass region require the selection of an appropriate nuclear interaction. This interaction is usually based on the extrapolation of a known nuclear interaction [2, 24, 29, 34], but this approach is fraught with uncertainty. In view of these uncertainties, the calculations can only provide qualitative results. These extrapolations and the associated model results become more uncertain as the system mass increases.
Table 1 summarizes previous calculations [21-37] in the 570 ≤ A < 1630 systems. The most stable (A, Z) system for the Ref. 21-37 calculations is provided in Table 1.
Table 1 also provides the alpha Q value for the most stable system, its effective half-life, and the interaction strength utilized. The calculations are based on the unmodified (λ = 1.0) Rost interaction [2], the modified (λ = 1.05) Rost interaction [24], adjusted (λ = 1.10) Rost interaction [29], and the Rost-1600 (λ = 1.15) interaction [34].
Table 1: Most Stable 570 ≤ A ≤ 1630 Nuclear Systems
Range |
(A, Z) |
Qα (MeV) |
T1/2eff |
λ |
570≤ A ≤ 620 |
(610, 204) |
16.2 |
2.2 h |
1.0a |
620< A < 700 |
(634, 204) |
17.8 |
0.14 s |
1.0b |
700≤ A < 800 |
(730, 226) |
20.0 |
0.44 s |
1.0c |
800≤ A < 900 |
(888, 274) |
19.5 |
590 y |
1.05d |
900≤ A < 1000 |
(926, 282) |
22.4 |
1.1 d |
1.05e |
1000≤ A < 1100 |
(1062, 312) |
23.8 |
152 d |
1.05f |
1100≤ A < 1200 |
(1122, 330) |
26.8 |
20 min |
1.05g |
1200≤ A < 1300 |
(1226, 354) |
21.6 |
4.8x1012 yr |
1.10h |
1300≤ A < 1400 |
(1344, 382) |
25.2 |
4.0x108 yr |
1.10i |
1400≤ A < 1500 |
(1478, 410) |
27.3 |
14 min |
1.10j |
1500≤ A < 1600 |
(1502, 414) |
26.6 |
2.9x1010 yr |
1.10k |
1600≤ A < 1610 |
(1602, 438) |
21.3 |
4.4x1032 yr |
1.15l |
1610≤ A < 1620 |
(1614, 438) |
24.0 |
6.3x1021 yr |
1.15m |
1620≤ A < 1630 |
(1626, 440) |
23.6 |
2.9x1023 yr |
1.15n |
a Ref. 21; bRef. 22; cRef. 23; dRef. 25; eRef. 26; fRef. 27; gRef. 28; hRef. 30; iRef. 31; jRef. 32; kRef. 33; lRef. 35, mRef. 36, and nRef. 37. |
Calculations for 1630 ≤ A < 1640 superheavy nuclei are presented in this paper. Model calculations suggest that 47 even-even nuclear systems theoretically exist within the 1630 ≤ A < 1640 mass range. The calculations utilized the Rost-1600 interaction [34].
1630 ≤ A < 1640 system stability is evaluated using the methodology utilized to investigate nuclear systems in the 570 ≤ A < 1630 [21-37] mass region. These calculations facilitate the investigation of superheavy systems that have received limited theoretical study, and provide insight into binding energy systematics and nuclear stability beyond the previously investigated mass regions.
Using a more sophisticated method than the single particle approach is not warranted in view of the uncertainties encountered in these calculations. These uncertainties include extrapolations of the nuclear interaction into the superheavy mass region. Since there are no experimental data to guide the calculations, single-particle energy level calculations are a reasonable approach for initial calculations into the superheavy mass region [3, 5].
The stability of 1630 ≤ A < 1640 system is determined by evaluating the various decay modes (i.e., alpha decay, beta decay, positron decay, electron capture, and spontaneous fission). Based on previous calculations [21-37], stability in the 1630 ≤ A < 1640 mass region is expected to be dominated by alpha decay and beta decay.
The model used to describe the particle (i) plus core (c) system represents an application of the standard method of Lukasiak and Sobiczewski [3] and Petrovich et al [5]. The calculational method used to generate a single particle level spectrum determines the binding energy ENLSJ of a particle in the field of a nuclear core by solving the radial Schrödinger Equation
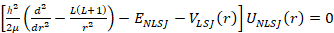 (1)
(1)
where r is the radial coordinate defining the relative motion of the nuclear core and the particle; VLSJ(r) is the model interaction; ENLSJ is the core plus particle binding energy; UNLSJ(r) is the radial wave function; and L, S, and J are the orbital, spin, and total angular momentum quantum numbers, respectively. N is the radial quantum number and μ is the reduced mass. For the present application, VLSJ is defined as:
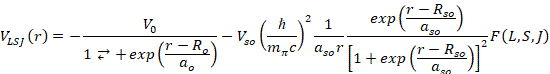
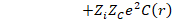 (2)
(2)
where
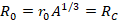 (3)
(3)
and
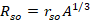 (4)
(4)
The parameters V0, r0, and a0 are the strength, radius parameter, and diffuseness for the central potential. Similarly, Vso, rso, and aso are the corresponding parameters for the spin-orbit potential. To complete the specification of Equation 2, we define:
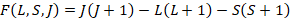 (5)
(5)
and
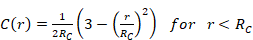 (6)
(6)
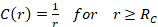 (7)
(7)
For the Coulomb potential, it is assumed that the particle is a point charge of magnitude zie. The core has a charge ZCe uniformly distributed through a sphere of radius RC. Since the potential is not a function of the spherical coordinates, the solution of the angular equation is most easily expressed in terms of spherical harmonics 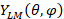 .
.
The total bound-state wave function 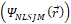 for the relative motion of the core plus particle, interacting through a spherically symmetric potential, is given by a product of space and spin wave functions:
for the relative motion of the core plus particle, interacting through a spherically symmetric potential, is given by a product of space and spin wave functions:
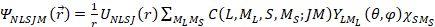 (8)
(8)
where ML and MS are the projections of angular momentum and spin, and χ is the spin wave function. For the calculation of single particle energy levels, N, L, S, and J specify the quantum numbers of the single particle level.
The binding energy of a single particle level is obtained by rewriting the radial Schrödinger equation in the form
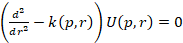 (9)
(9)
where
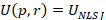 (10)
(10)
and
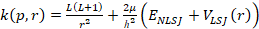 (11)
(11)
The model searches for values of the parameter p in order to obtain the binding energy ENLSJ for a given potential. The method of searching for p is provided by Brown, Gunn, and Gould [38] using the methodology of Ref. 39 to obtain a converged solution. Refs. 2, 3, 5, and 21-40 provide additional details of the model, numerical methods, and associated interactions.
Determination of Q Values and Half-Lives
Given the uncertainties in the nuclear interaction, calculated half-life values only represent relative values. The largest values suggest regions of possible stability relative to other systems whose properties are calculated with the same interaction.
Table 2 provides the Q value for alpha decay and the alpha and beta decay half-lives for 1630 ≤ A < 1640 superheavy nuclei having effective half-lives ≥ 1021 yr based on the Rost-1600 interaction [34]. Alpha decay energies are calculated using the relationship
Qα = 28.3 MeV -2 Sn -2 SP (12)
In Equation 2, Sn and Sp are the binding energies of the last occupied neutron and proton single-particle energy levels, respectively [1]. The alpha decay, beta decay, positron decay, and electron capture half-lives were determined following the methodology noted in Ref. 3.
Table 2: Calculated Properties for 1630 ≤ A < 1640 Nuclei
Nucleus |
Tβ1/2(yr) |
Qα (MeV) |
Tα1/2(yr) |
442 |
1188 |
a |
23.7 |
2.1E+23 |
444 |
1186 |
a |
24.2 |
2.0E+22 |
446 |
1184 |
a |
24.7 |
2.1E+21 |
442 |
1190 |
a |
23.6 |
6.0E+23 |
444 |
1188 |
a |
24.1 |
5.6E+22 |
446 |
1186 |
a |
24.5 |
5.5E+21 |
442 |
1192 |
a |
23.5 |
1.7E+24 |
444 |
1190 |
a |
23.9 |
1.6E+23 |
446 |
1188 |
a |
24.4 |
1.5E+22 |
442 |
1194 |
a |
23.3 |
4.9E+24 |
444 |
1192 |
a |
23.8 |
4.3E+23 |
446 |
1190 |
a |
24.2 |
4.1E+22 |
448 |
1188 |
a |
24.7 |
4.2E+21 |
442 |
1194 |
a |
23.3 |
4.9E+24 |
444 |
1192 |
a |
23.8 |
4.3E+23 |
446 |
1190 |
a |
24.2 |
4.1E+22 |
448 |
1188 |
a |
24.7 |
4.2E+21 |
442 |
1196 |
a |
23.2 |
1.4E+25 |
444 |
1194 |
a |
23.6 |
1.2E+24 |
446 |
1192 |
a |
24.1 |
1.1E+23 |
448 |
1190 |
a |
24.5 |
1.1E+22 |
aBeta stable. |
Allowed (first-forbidden) beta decay half-lives are obtained from the values of log ft = 5 (8) [1]. In view of the uncertainties in the calculated level energies, second and higher forbidden transitions were not determined. The beta half-lives summarized in Table 2 listed as stable are either beta stable or decay by these higher orders forbidden transitions.
The single-particle level spectrum is generated using a Woods-Saxon potential with parameters optimized to permit extrapolation into the A ≥ 1600 superheavy region [34]. Based on the calculations summarized in Ref. 34, a 15% uncertainty in the potential strength of the Rost interaction [2] was judged to be reasonable.
The 15% potential strength uncertainty is incorporated into the Rost-1600 interaction [34].
V0 = 51.6 [1 ± 0.73 (N – Z)/A] MeV (13)
with λ = 1.15. Calculated single-particle energies are also derived by incorporating the unmodified pairing interaction of Blomqvist and Wahlborn [40] to investigate the bounding characteristics of A ≥ 1600 superheavy nuclear systems.
The Rost-1600 model results should only be compared to calculations based upon this interaction. It is not appropriate to compare the Rost-1600 calculations with calculations based on the Rost interaction and its other variants [2, 24, 29] for 570 ≤ A<1600 [5, 21-23, 25-28, 30-33]. A comparison to the heavier 1600 ≤ A < 1630 mass region [35-37] is provided in Table 1. The A<1600 systems noted in Table 1 are only presented for information.
Figures 1 and 2 presents relevant calculational results for the bound 1630 ≤ A < 1640 even-even nuclei considered in this paper. The effective half-life (Equation 4) for nuclei with 1630 ≤ A < 1640 is illustrated in Figure 1. Most 1630 ≤ A < 1640 nuclei decay through both alpha and beta emission. The Qα values for nuclei with 1630 ≤ A < 1640 are plotted in Figure 2.
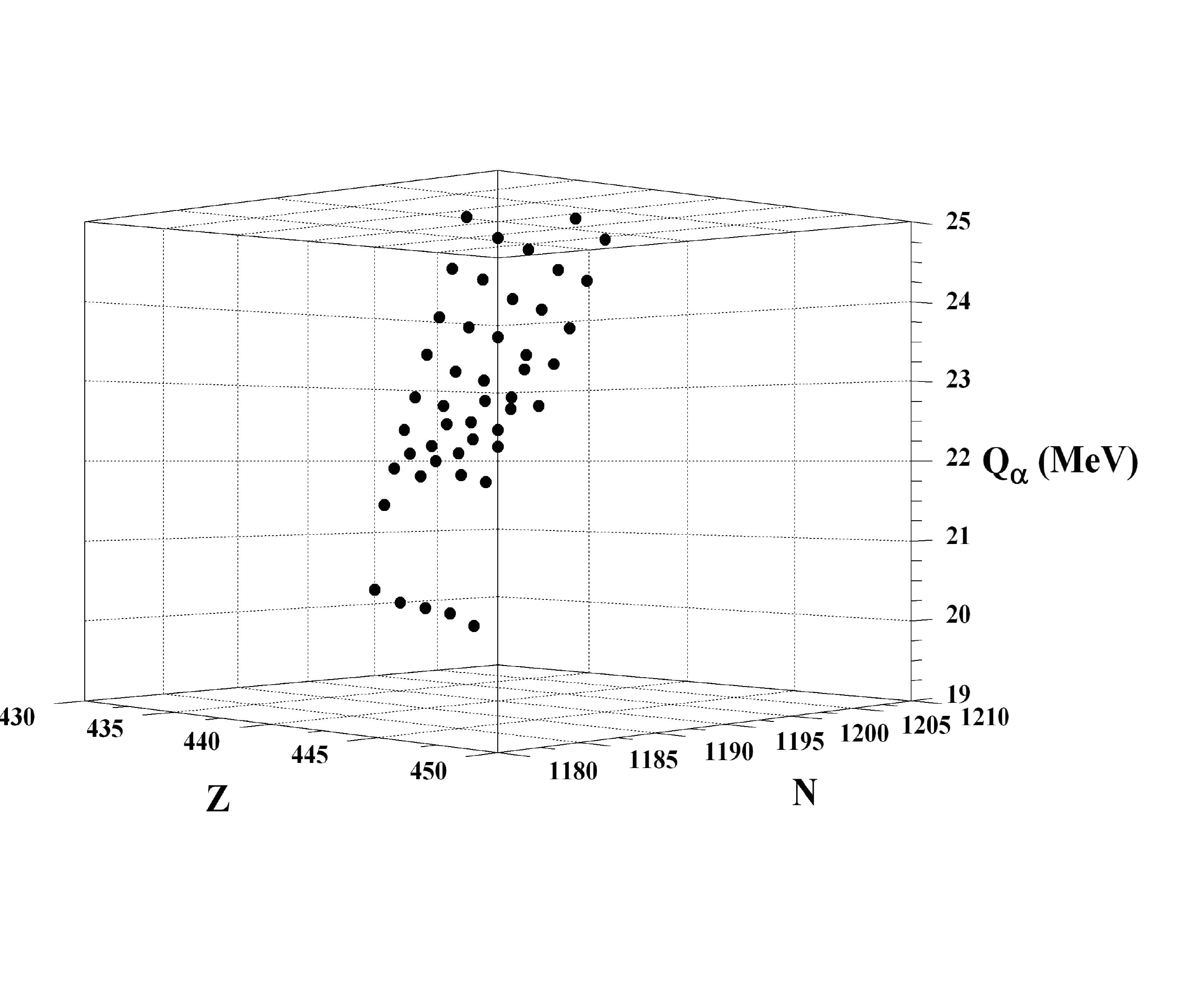
Figure 1. Three-dimensional plot of the effective half-life (T1/2eff) as a function of N and Z for 1630 ≤ A < 1640 nuclear systems. To simplify the plot, the half-lives of the systems summarized in Table 2 with half-lives > 1021 yr are depicted as 10-6 yr rather than their actual values. Using the actual half-life values would compress most of the figure causing a loss of detail.
Figure 2. Three-dimensional plot of the Qα values as a function of N and Z for 1630 ≤ A < 1640 nuclear systems.
The stability of any bound superheavy nucleus is dependent on its shell structure. Closed-shell effects [3, 5, 21-37] tend to enhance the stability of a nuclear system. The importance of these shell effects is noted in subsequent discussion.
A new island of stability in the vicinity of Z = 442 - 448 (See Table 2) is suggested for 1630 ≤ A < 1640 systems. The most stable 1630 ≤ A < 1640 system is the (442, 1638) nucleus that has partially filled 1u33/2 neutron and 1o25/2 proton shells. This system is stable with respect to beta decay, and has an alpha decay half-life of 1.4x1025 yr.
Table 2 summarizes a subset of the 47 bound nuclei within 1630 ≤ A < 1640 systems that have effective half-lives ≥ 1021 yr. The effective half-life, including the combined effect of the alpha and beta decay modes, is defined as
T1/2eff = (Tα1/2 Tβ1/2) / (Tα1/2 + Tβ1/2) (14)
As noted in Fig. 1, many of the 1630 ≤ A < 1640 systems have effective half-lives less than ~10-4 s, and beta decay through allowed 4j15/2(n) to 2j13/2(p) and 2o25/2(n) to 1o25/2(p) transitions.
Based on previous calculations [21-37], spontaneous fission stability is expected to be enhanced near doubly-closed shells. These spontaneous fission calculations utilized the Wentzel-Kramers-Brillouin (WKB) approximation methodology and the phenomenological parameter values of Ref. 3. The calculations suggest that fission half-lives near closed shells are greater than the effective decay half-lives calculated using Equation 4 [21-37].
There are level systematics that are consistent with previous calculations [21-37]. For a given A value, Sp tends to decrease and Sn tends to increase as Z increases. These conditions lead to increasing Qα values as Z increases for a fixed A value.
The systematics involved in the beta decay transitions are more complex. These depend on selection rules that depend on a number of considerations including (1) the occupancy of specific single-particle levels, (2) single-particle level quantum numbers, and (3) single-particle energy level values that permit an allowed or forbidden transition to occur.
Specific trends in alpha and beta half-lives are consistent with previous calculations [21-37]. If the A value is fixed, alpha decay half-lives tend to decrease and beta decay half-lives tend to increase as Z increases. For a fixed Z, alpha decay half-lives tend to increase and beta decay half-lives tend to decrease as A increases.
In the 1630 ≤ A < 1640 system, most decays occur through both alpha and beta pathways. Most of the calculated 1630 ≤ A < 1640 half-lives are shorter than the longest-lived Z = 114 – 118 nuclei [41], but Table 2 notes several long-lived exceptions. These systems are likely an artifact of the Rost-1600 interaction. However, the systems summarized in Tables 1 and 2 suggest possible islands of nuclear stability.
Model limitations include uncertainties in the nuclear interaction [2, 24, 29, 34], exclusion of nonconventional decay modes that could exist in superheavy systems [21-37], and treating all system as spherically symmetric nuclei [21-37]. The model uncertainties prevent the determination of specific single-particle energies, Q values, and half-lives. However, the proposed model permits a comparison of the relative stability of nuclear systems and determination of possible islands of nuclear stability [41].
The accuracy of the proposed model can be partially addressed by comparing the (Z, A) values of calculated system properties to the predictions of Adler’s relationship [42, 43]. The Alder relationship provides the most stable nucleus Z value for a given A:
Z = (0.487 A) / (1 + A2/3 /166) (15)
This relationship can be compared to the model predictions for the most stable 1630 ≤ A < 1640 nucleus. When applied to the (442, 1638) system, the Adler relationship predicts that the most stable A = 1638 Z value is 434. This is about 2% smaller than the Z = 442 result obtained from the spherical model outlined in this paper. This comparison between the model and predictions of the Adler relationship of Equation 5 suggests at least the qualitative success of the proposed model.
The creation of elements with Z > 118 has yet to be successful. Production of A ≥ 1600 systems is more complex than the challenge of creating Z > 118 nuclei.
Binary collision processes involving heavy ions beams are not currently capable of reaching the 1630 ≤ A < 1640 mass region. Creating these systems will require an unconventional approach (e.g., colliding multiple 238U ions).
The alpha particle energies of the theoretical 1630 ≤ A < 1640 systems are greater than twice the Z = 114-118 values [41]. A measurable track length is produced when an alpha particle traverses a medium [43, 44]. Since the track length is related to the alpha particle energy, it provides a possible method to verify the existence of a 1630 ≤ A < 1640 superheavy system.
An additional verification method is based on the fact that various lead isotopes are the endpoint of known natural decay chains (e.g., 232Th, 235U, and 238U) [43, 44]. This observation suggests that lead targets could be vaporized, accelerated, and then separated by mass. The remnants of a long-lived parent superheavy nuclei summarized in Tables 1 and 2 could be present in the mass spectrum [45].
Previous calculations explored the 570 ≤ A < 1630 mass region, and this paper extends these calculations to 1630 ≤ A < 1640. The single-particle level spectrum is generated using a Woods-Saxon potential with parameters optimized to permit extrapolation into the A ≥ 1600 superheavy region utilizing the Rost-1600 interaction that was based on existing nuclear systems as well as nuclear matter calculations. This interaction is essentially the Rost interaction that includes a 15% uncertainty in the potential strength. Calculated single-particle energies are also derived by incorporating the unmodified pairing interaction of Blomqvist and Wahlborn to investigate the bounding characteristics of A ≥ 1600 superheavy nuclear systems.
Given uncertainties in the model interaction, it is not practical to determine absolute values for the half-lives and Q-values. However, the model does permit establishing the relative stability of nuclear systems and to highlight possible islands of stability.
Model limitations include uncertainties in the nuclear interaction, exclusion of nonconventional decay modes that could exist in superheavy systems, and treating all system as spherically symmetric nuclei. The model uncertainties prevent the determination of specific single-particle energies, Q values, and half-lives. However, the proposed model permits a comparison of the relative stability of nuclear systems and determination of possible islands of nuclear stability.
The stability of 1630 ≤ A < 1640 systems are determined by evaluating the various decay modes (i.e., alpha decay, beta decay, positron decay, electron capture, and spontaneous fission). Stability in the 1630 ≤ A < 1640 mass region is dominated by alpha decay and beta decay.
The accuracy of the proposed model can be partially addressed by comparing the (Z, A) values of calculated system properties to the predictions of Adler’s relationship. The Alder relationship provides the most stable nucleus Z value for a given A. This relationship can be compared to the model predictions for the most stable 1630 ≤ A < 1640 nucleus. When applied to the (442, 1638) system, the Adler relationship predicts that the most stable A = 1638 Z value is 434. This is about 2% smaller than the Z = 442 result obtained from the spherical model outlined in this paper. This comparison between the model and predictions of the Adler relationship of Equation 5 suggests at least the qualitative success of the proposed model.
Using the Rost-1600 interaction, 47 even-even nuclear systems are predicted in the 1630 ≤ A < 1640 mass region. For this mass region, the model predicts a new island of stability in the vicinity of the Z = 442 – 448. It is stable with respect to beta decay, and has an alpha decay half-life of 1.4x1025 yr. (442, 1638) has partially filled 1u33/2 neutron and 1o25/2 proton shells.
- C. Y. Wong (1996) Additional evidence of stability of the superheavy element 310126 according to the shell model. Phys. Lett 21: 688.
- E. Rost (1968) Proton Shell-Model Potentials for Lead and the Stability of Superheavy Nuclei. Phys. Lett 26B: 184.
- A. Lukasiak., A. Sobiczewski (1975) Estimations of half-lives of far-superheavy nuclei with Z approx. = 154 – 164. Acta Phys Pol B6: 147.
- R. V. Gentry., T. A. Cahill., N. R. Fletcher., H. C. Kaufmann, L. R. Medsker., et al. (1976) Flocchini, Evidence for Primordial Superheavy Elements. Phys. Rev. Lett 37: 11.
- F. Petrovich., R. J. Philpott., D. Robson, J. J. Bevelacqua, M. Golin., et al. (1976) Comments on Primordial Superheavy Elements. Phys. Rev. Lett 37: 558.
- G. N. Flerov., G. M. Ter-Akopian (1983) Superheavy Nuclei. Rep. Prog. Phys 46: 817.
- R. Smolańczuk (1997) Properties of the hypothetical spherical superheavy nuclei. Phys. Rev C 56: 812.
- M. Bender, K., Rutz., P.-G. Reinhard., J. A. Maruhn., W. Greiner (1998) Potential energy surfaces of superheavy nuclei. Phys. Rev C 58: 2126.
- S. Hofmann., G. Münzenberg (2000) The discovery of the heaviest elements. Rev. Mod. Phys 72: 733.
- S. B. Duarte., O. A. P. Tavares., M. Gonçalves., O. Rodríguez., F. Guzmán., et al. (2004) Half-life predictions for decay modes of superheavy nuclei. J. Phys. G: Nucl. Part. Phys 30: 1487.
- H. Koura., T. Tachibana., M. Uno., M. Yamada (2005) Nuclidic Mass Formula on a Spherical Basis with an Improved Even-Odd Term. Prog. Theor. Phys. 113: 305.
- P. Mohr (2006) α-nucleus potentials, α-decay half-lives, and shell closures for superheavy Nuclei. Phys. Rev C 73: 031301(R).
- Yu. Ts (2006) Oganessian et al, Synthesis of the isotopes of elements 118 and 116 in the 249Cf and 245Cm + 48Ca fusion reactions. Phys. Rev C 74: 044602.
- P. R. Chowdhury., C. Samanta., D. N. Basu (2008) Search for long lived heaviest nuclei beyond the valley of stability. Phys. Rev C 77: 044603.
- C. Samanta (2009) Alpha decay chains from superheavy nuclei. Prog. Part. Nucl. Phys 62: 344.
- P. Möller., A. J. Sierk., T. Ichikawa., A. Iwamoto., R. Bengtsson., et al. (2009) Heavy-element fission barriers. Phys. Rev C 79: 064304.
- A. Marinov (2010) Evidence for the Possible Existence of a Long-Lived Superheavy Nucleus with Atomic Mass Number A = 292 and Atomic Number Z ≅ 122 in Natural Th. Int. J. Mod. Phys E 19: 131.
- D. N. Poenaru., R. A. Gherghescu., W. Greiner (2011) Heavy-Particle Radioactivity of Superheavy Nuclei. Phys. Rev. Lett 107: 062503.
- Yu. Ts. Oganessian (2012) Production and Decay of the Heaviest Nuclei 293,294117 and 294118. Phys. Rev. Lett 109: 162501.
- K. Morita (2012) New Result in the Production and Decay of an Isotope, 278113, of the 13th Element. J. Phys. Soc Japan 81: 103201.
- J. J. Bevelacqua (2012) 570 ≤ A ≤ 620 Superheavy Nuclei. Physics Essays 25: 475.
- J. J. Bevelacqua (2013) Superheavy Nuclei II: 620 < A < 700 Systems. Physics Essays 26: 516.
- J. J. Bevelacqua (2014) Superheavy Nuclei III: 700 ≤ A < 800 Systems. Physics Essays 27: 655.
- J. J. Bevelacqua (2015) Bounding Potential for Studies of A ≥ 800 Superheavy Nuclei. Physics Essays 28: 300.
- J. J. Bevelacqua (2016) Superheavy Nuclei IV: 800 ≤ A < 900 Systems. Physics Essays 29: 490.
- J. J. Bevelacqua (2017) Superheavy Nuclei V: 900 ≤ A < 1000 Systems. Physics Essays 30: 1.
- J. J. Bevelacqua (2017) Superheavy Nuclei VI: 1000 ≤ A < 1100 Systems. Physics Essays 30: 392.
- J. J. Bevelacqua (2018) Superheavy Nuclei VII: 1100 ≤ A < 1200 Systems. Physics Essays 31: 235.
- J. J. Bevelacqua (2018) Candidate Potential for Studies of A ≥ 1200 Nuclei. Physics Essays 31: 377.
- J. J. Bevelacqua (2020) Superheavy Nuclei VIII: 1200 ≤ A < 1300 Systems. Physics Essays 33: 276.
- J. J. Bevelacqua (2021) Superheavy Nuclei IX: 1300 ≤ A < 1400 Systems. Physics Essays 34: 54.
- J. J. Bevelacqua (2022) Superheavy Nuclei X: 1400 ≤ A < 1500 Systems. Qeios EIVJC0 1.
- J. J. Bevelacqua (2022) Superheavy Nuclei XI: 1500 ≤ A < 1600 Systems. Qeios HQ0MAW 1.
- J. J. Bevelacqua (2013) Candidate Potential for Studies of A ≥ 1600 Superheavy Nuclei. Qeios 3IGK15 1.
- J. J. Bevelacqua (2023) Superheavy Nuclei XIII: 1600 ≤ A < 1610 Systems. Qeios EKHBBT 1.
- J. J. Bevelacqua (2024) Superheavy Nuclei XIV: 1610 ≤ A < 1620 Systems Qeios HXUFBF 1.
- J. J. Bevelacqua (2024) Superheavy Nuclei XV: 1620 ≤ A < 1630 Systems. Qeios GVLLOY 1.
- G. E. Brown., J. H. Gunn., P. Gould (1963) Effective mass in nuclei. Nucl. Phys 46: 598.
- L. Fox., E. T. Godwin (1949) Some new methods for the numerical integration of ordinary differential equations. Proc. Cambridge Philos. Soc 45: 373.
- J. Blomqvist., S. Wahlborn (1959) Shell model calculations in the lead region with a diffuse nuclear potential. Ark. Fys 16: 545.
- E. M. Baum., M. C. Ernesti., H. D. Knox., T. R. Miller., A. M. Watson (2010) Nuclides and Isotopes – Chart of the Nuclides. 17th ed.
- K. Adler (1972) Coulomb Interactions with Heavy Ions, CONF-720669, Proceedings of the Heavy Ion Summer School. Oak Ridge TN.
- J. J. Bevelacqua (2009) Contemporary Health Physics: Problems and Solutions. 2nd ed.
- J. J. Bevelacqua (2010) Basic Health Physics: Problems and Solutions. 2nd ed.
- J. J. Bevelacqua (2020) Proposed Mass Spectrometry Method to Facilitate the Observation of Primordial Superheavy Nuclei. QEIOS QATSLS 1.

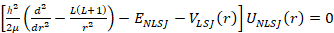
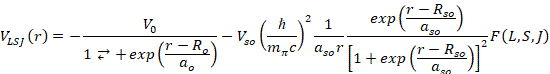
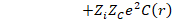
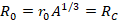
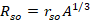
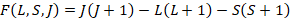
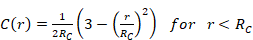
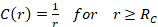
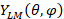 .
.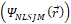 for the relative motion of the core plus particle, interacting through a spherically symmetric potential, is given by a product of space and spin wave functions:
for the relative motion of the core plus particle, interacting through a spherically symmetric potential, is given by a product of space and spin wave functions: