Abstract

The aim of this paper is to explain the historical inconsistencies that arise from the lack of definition of the wave function in Edwin Schrödinger’s wave equations that concomitantly give rise to uncertainty as to whether or not the quantum superposition state has random or deterministic properties. A redefinition of the wave function is given that is in coherence with quantum research into the double slit experiment. This new definition includes its deterministic character and expounds the specific parameters that constitute the eight hidden variables held within the dual space that is the quantum superposition state.

Key Words

Schrödinger’s Wave Equation; Wave Function; Spin, Hidden Variables; Superposition

Introduction

The intention of this work is to explain how the historical misperceptions regarding the phenomenon of the quantum wave function have arisen as given in the Schrödinger’s wave equations. The results of the double slit experiment are used to demonstrate the validity of this new definition and the resulting observation of the wave and particle states being discrete.

Discussion

The current definition of a wave function is a mathematical description of a quantum system giving the probability amplitude, the square of which provides the probability density of finding a particle at a particular location at a particular time. In Schrödinger’s wave equation, the Greek letter Ψ (psi) is used as the symbol to represent the wave function. In this way every particle can be represented as an expression of Ψ (i.e. - momentum and time) [1].

Initially, the concept of a wave function arose from the Schrödinger wave equation which describes how the quantum state of a physical system changes with time. It is a predictive equation that demonstrates the evolution of the wave state over time within the quantum state. However, in his wave equations, Edwin Schrödinger never actually defined what the wave function was. The task of assigning a clear definition of a wave function was taken up later by Max Born in 1926 that developed “Born’s rule” from Schrödinger’s wave equations. This law states that the probability density of finding a particular particle at a particular location at a specific time can be established by squaring the wave function, which is the same as squaring the probability amplitude – Ψ². Thus in Born’s rule, the wave function is defined as the square of the probability amplitude. So historically, quantum physics has taken on board the definition of the wave function as being directly related to the probability amplitude. This definition is still in place today.

Historical Misperception

One of the most salient remarks to make in the chequered history of quantum physics is that the Schrödinger wave equation defines the state of a physical system – i.e. a quantum state that is comprised of both a wave AND a particle with a time-dependent state. However, it is important to appreciate the fact that the state in which both a wave and a particle exist is in the collapsed state in the quantum scale, not the superposition state.^[1]. This is a very subtly nuanced point to make, but nonetheless a very important one, in order to correctly understand the exact dynamics of a quantum system, that both waves and particles (which have discrete state of special unitary symmetry – wave = SU(3) and particle = SU(2)) [2] actually only exist in the collapsed state (i.e. observed) and not in the superposition state (i.e. unobserved state).

Below is a diagram that shows the current perception of a wave function:

Figure 1: Current Perception of the Wave Function

It can be noted in the above diagram that the wave function before detection takes the form of a wave – i.e. that the wave exists in the superposition state AND in the collapsed state. I strongly disagree with this interpretation and am providing another diagram of a wave function that more accurately describes its state - (i.e. the state before observation/detection):

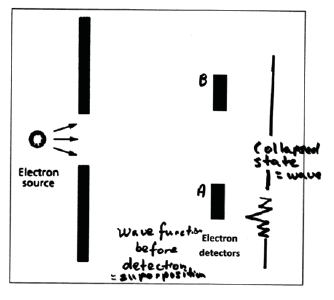
Figure 2: Real Time Wave Function-No Wave or Particle State

It can be noted that in Figure 2 above that there is nothing perceptible in the state before detection–i.e. the superposition state is imperceptible and contains nothing visible; no energy or matter whatsoever. It contains no wave state and no particle state. It is my strong view that the above diagram of the superposition state more accurately describes the state prior to observation. This state is non-local in character and contains no wave or particle state. It is both without motion and form. In other words, the state before detection does not exist on either the imaginary (wave state) or real (particle state) planes. There is no motion or form in the superposition (pre-observed) state. It is this historical misperception that I wish to correct in this paper. Since Edwin Schrödinger’s intention was to describe the wave state over time, which is not the same process as describing the superposition state (i.e. pre-observed state). No, the Schrödinger wave equation describes the evolution of the wave state over time but it does not describe the superposition state. There are four important misperceptions I wish to correct about the Schrödinger wave equation in this paper. These are:

1. That it describes the superposition state = wave function before observation.
2. That the superposition state contains both waves and particles.
3. That it suggests that a particle can be simultaneously in two locations.
4. That the particle state is simultaneously a wave state in a quantum system.

The superposition state is NOT the state that the Schrödinger wave equations describe. Schrödinger wave equations are equations of motion since they describe the wave state. They are not equations of abstraction (superposition state) or state of rest (particle state).

The superposition state is not the probability amplitude, since the probability amplitude describes a wave state which cannot exist in the pre-observed state, since the wave state represents the kinetic energy of a quantum system, whilst in the pre-observed state there is no kinetic energy, no actual motion taking place, only the potential for motion. The superposition state is an informational state that exists on the abstract and complex planes. It contains the information sets that will give rise to both the wave and particle states. These two informational sets each contain information subsets. The informational sets are intrinsic angular momentum or spin quantum number (m_s) and total angular momentum or magnetic quantum number (m_l). Upon observation, the superposition state collapses to the states of the wave, taking the form of angular velocity – ω = principal quantum number from the state of total angular momentum - m_l and also the particle, taking the state of orbital angular momentum or azimuthal quantum number from the state of intrinsic angular momentum - m_s.

Below is a diagram that I propose more accurately depicts the superposition state and the collapsed state showing the angular momenta and quantum number states within a quantum system:

Figure 3: Annotated Superposition and Collapsed States of a Quantum System

Thus, it can be understood that the real wave function state represents the state before detection-i.e. before quantum collapse. Currently, there is a confused cross-wires explanation of the wave function that defines it as being associated with both the probability amplitude of the Schrödinger wave equation as well as the superposition state and not purely representing the superposition state as it needs to be. Schrödinger never defined what a wave function truly was and its definition has become incorrectly associated with the concept of a probability amplitude, which itself has arisen from an erroneous view of the wave-particle duality. Further complicating matters, Max Born’s rule does not describe the wave function, but describes the probability density born out of the Schrödinger wave equation. The wave function is not the probability amplitude, since the issue of probability amplitude itself is erroneous, as a single particle cannot exist in two discrete states of space simultaneously as the Fermi-Dirac statistics attest. They can only exist in one field state at a time.

The current understanding of the superposition state is that it is a state in which both a wave and a particle state can exist. I propose that this is incorrect. Neither a wave nor a particle can exist in the unobserved state, since the superposition state operates on the abstract and complex planes. The superposition state does not operate on the imaginary plane where the wave state exists, nor on the real plane where the particle state exists. Only the informational blueprint, abstract template or hidden variables of the wave and particle states exist and I propose that this template operates on the abstract plane (spin) and complex plane (total angular momentum). The wave function is an informational state that contains eight hidden variables that operate as different trajectories that can be selected or chosen, depending on the external environment in which the quantum superposition state is found. Yes, this can perhaps be described as a process of natural selection, albeit at the quantum scale.^[2] I suggest that the external environment can be a state of specific unitary symmetry.

We must never forget the fact that Edwin Schrödinger never actually defined the wave function, so for Max Born to boldly declare that Born’s rule was based on the Schrödinger wave equations for which there was no definition of a wave function provided, is based on shaking ground indeed! In my view, it is preferable to totally omit the term “wave function” from both the Schrödinger wave equations as well as the born rule and replace it with the term “probability amplitude”. This will provide a more accurate description of a quantum state from Schrödinger’s perspective. However, given the fact that Schrödinger believed that a particle can exist in the superposition state, which in turn gives rise to the whole plethora of problems associated with the subject of probability, (including dead or alive cats in boxes), in real terms this makes his wave equations highly questionable, despite their mathematical elegance.

Below is a summary of the information relating to the relationship of the wave equation to the Schrödinger equation as it pertains to this paper.

The three main wave states can be appropriated to Schrödinger equations in this way:

Time independent Schrödinger equation                              =standing wave states
Time dependent Schrödinger equation (non-relativistic)     =transverse wave state

Time dependent Schrödinger equation (general)                 =longitudinal wave state

Wave function ≠ probability amplitude                                   = superposition state

Superposition state = information of hidden variables of m_s:m_l = wave function = Ψ
       = m_s = spin quantum number = intrinsic angular momentum
      = m_l = magnetic quantum number = total angular momentum
      = unobserved/undetected state
      = exists on the abstract (m_s) and complex (m_l) planes
      = Schrödinger wave equations do not apply
      = contains no wave nor particle state
      = is a dual-space informational state containing the states of information at rest (m_s) and information in potential (m_l).
Collapsed state = wave and particle state. These are discrete states that operate on a

       Different statistical basis –
       i.e. Bosé-Einstein statistics (boson) and Dirac-Fermi statistics (fermion)
      = Schrödinger wave equations apply
      = observed/detected state
      = wave state = n = principal quantum number = angular velocity (w)
      = particle state = l = azimuthal quantum number = orbital angular momentum

Correct Definition

Now that the historical misperceptions have been illustrated, I will begin to explain how the wave function needs to be redefined in order to more accurately reflect the dynamics of the quantum state in real terms. Here is the new definition of a wave function that I propose:

“A wave function is an informational dual space of the unobserved quantum superposition state which, upon observation, gives rise to the collapse of the quantum superposition state, to produce the discrete wave and particle states. The information of the wave function is in the form of intrinsic angular momentum (m_s) and total angular momentum (m_l), each of which hold four parameters embedded within them, that together represent the sum of eight hidden variables. This informational state of the wave function is a deterministic state that represents the phenomenon of the quantum superposition state.”

I do not believe that the wave function is the probability amplitude. I think it would be a good idea from this point forward, to change the symbol of the probability amplitude – ψ psi, to ⇝ in order to accurately reflect the difference between the wave function (deterministic superposition state = ψ) and the Schrödinger wave function (probability wave state = ⇝).

From my perspective, it needs to be conventionally agreed that the wave function describes the information of the superposition state which holds the eight hidden variables of spin and total angular momentum or m_s and m_l respectively. These two parameters each have their own variables hidden within them – four for spin and four for total angular momentum. These hidden variables can be considered to be different possible states that exist on the abstract (m_s) and complex planes (m_l) in the unobserved superposition state that, upon observation, can take the form of either a wave or a particle. I will now explain each of these eight hidden variable states.

The state of spin or intrinsic angular momentum (m_s) has four possible states which are as follows:

1. spin up (left hand chirality)
2. spin up (right hand chirality)
3. spin down (left hand chirality)
4. spin down (right hand chirality)

Each of these four spin states represents a different spin state that the particle can take upon collapse, providing four different hidden variables of spin that exist in the superposition state. Similarly, I propose that the state of total angular momentum (m_l) also has four possible states that are also held in the superposition state which can be extrapolated from the formula for total angular momentum J = L + S, where:

J = total angular momentum
L = orbital angular momentum and
S = spin or intrinsic angular momentum.

It can be understood that each of the states of L (orbital angular momentum) and S (spin) has two possible parameters as follows:

L = orbital angular momentum has two variable states:

1. Internal angular momentum
2. External angular momentum [3].

S = intrinsic angular momentum has two variable states:

1. Left circular polarisation

Right circular polarization [4].

Therefore it can be demonstrated that the state of total angular momentum also has four different variable states that exist as hidden variables within the superposition state. These four hidden variables of total angular momentum, together with the four hidden variables of intrinsic angular momentum combine to make a total of eight hidden variables.

To explain the superposition diagrammatically, we can consider that each of the two states of spin and total angular momentum exist on their own individual axis. Thus the superposition state can be perceived as consisting of two diagonal axes that are perpendicular to each other: –k/k and j/-j with intrinsic angular momentum or spin (m_s) exists on the –k/k axis and the state of total angular momentum (m_l) existing on the j/-j axis.

Below is an annotated diagram showing the four hidden variables of intrinsic angular momentum (m_s) (shown in grey) on the –k/k axis and the four hidden variables of total angular momentum (m_l) (shown in green) on the j/-j axis, giving a total of eight hidden variables.

Figure 4: Diagram of the Eight Hidden Variables in the Superposition of Spin and Total Angular Momentum

The recent work in July 2016 by Polish physicists who developed a hologram of a single photon shows that a photon consists of four regions in the shape of a Maltese cross that are embedded within a dark background [5]. I propose that the four regions of darkness between each of the four sections of the cross depict the four states of spin or intrinsic angular momentum as shown in the left image below in Figure 5, and that the four red regions depict the four states of total angular momentum as shown in the right image below in Figure 5.^[3] This diagram depicts the four hidden variables for each of the states of spin and total angular momentum – i.e. the eight hidden variables that are at the heart of quantum determinism.

Figure 5: Diagram of Single Photon Hologram Showing Four Hidden Variables of Spin (Left Image) and Four Hidden Variables of Total Angular Momentum (Right Image)

Conclusion

To accurately continue the field of quantum research, I believe we must return to the pre-Schrödinger phase in the evolution of quantum physics and revive Einstein’s concept of quantum determinism and its associated hidden variables that exist within the superposition state. It is these eight hidden variables within the quantum superposition state that determines how the wave state actually functions - hence the term “wave function”. I also propose that these eight hidden variables are directly related to the gluon octet of quantum chromo dynamics, with each variable being attributed to a particular gluon state. These eight hidden variables represent the “master plan” or informational sets that contain the data to create both a wave and a particle state upon observation. They are a pre-determined informational set of values and vectors, which are available to be chosen depending on the external environment.

It is very true that the Schrödinger wave equations accurately describe wave states, and they do so brilliantly. However, they do not describe the particle state. This is the reason why they do not predict the reality of a single particle state at a particular location in space and moment of time, because they are wave equations not particle equations. The definition of a wave in classical mechanics is: “a disturbance in a medium that transports energy, but not matter” [6]. The definition of a wave in the classical state is no different to the quantum state. Waves do not carry particles. They carry energy and are not inertial as particles are. They describe energy transportation. This is the function of the wave state–to transport energy. The function of the particle state is to store energy in a potential and inertial state.

There is no doubt that the Schrödinger equations do indeed predict the evolution of the wave state under different conditions. They accurately predict the wave state with great mathematical precision and elegance. However, it is important to appreciate the fact that the question of whether or not the particle states exist within the actual wave itself is a very salient point to make. I believe it is an unreal expectation that the particle state exists within the wave state. This is one of the issues I am addressing in this paper. The Schrödinger equations do not predict the reality of the actual particle state. The particle and the wave states act independently of each other in separate non-abelian symmetry groups [1] and since the particle state cannot exist in the superposition by virtue of its asymmetrical special unitary symmetry group of SU(2), then the question of the probability state does not arise. Hence, whilst the Schrödinger equations predict waves mathematically, they do not predict them in real terms, since the particle state does not exist in either the superposition state nor within the actual wave itself. That is to say the particle is not part of the structure of the wave state. It exists in a separate non-abelian special unitary symmetry group of SU(2) which is independent to the wave state of the non-abelian unitary symmetry group of SU(3). It may appear that electrons have wave states since a beam of electrons can indeed be diffracted, but this phenomenon is due to the fact that all three types of electron beams are generated by SU(3) phenomena (see footnote below)[[4], 7, 4] and since the wave state itself also belongs to the special unitary symmetry group of SU(3), then it can be appreciated that the beam of electrons is diffracted into a wave state due to the SU(3) initial emission condition that gives rise it. For example, it is the causative phenomenon of heat in thermionic emission that causes the diffraction of an electron beam, not the electron particle itself. In this way, the concept of wave-particle duality that has arisen from the erroneous understanding of the cause of electron beam diffraction.

Thus I propose that the real definition of a wave function (ψ) is indeed the state of quantum superposition or unobserved quantum state. This state holds the eight hidden variables of the states of intrinsic angular momentum (m_s) and total angular momentum (m_l). These states are also known as the spin quantum number (m_s) and magnetic quantum number (m_s) respectively. This definition provides us with the much needed differentiation between the superposition and collapsed states in a quantum system and also removes any confusing implication of a particle state being present within the wave state (which it simply cannot since the wave and particle states are intrinsically discrete).

By transforming the definition of a wave function to explain that it can only ever exist in the superposition state and contains no actual wave state or state of motion or particle state, we can thus leave the vexed issue of probability amplitude totally out of the equation (pun intended!). In fact we can totally remove the association of the term “wave function” with the Schrödinger wave equation and let the symbol ⟿ represent the probability amplitude within the context of the Schrödinger wave equation, since the reality of the phenomenon of probability amplitude in the superposition state does not actually exist.^[5]. In this way the concept of a wave function becomes a description of the deterministic superposition state with its eight hidden variables within the states of spin and total angular momentum and therefore can in no way be associated with Schrödinger’s wave equations.

The historical misperceptions that have arisen regarding the wave function brought about by the concepts of quantum physics as perceived by Edwin Schrödinger, Neils Bohr and Max Born have unfortunately been carried through to the present day interpretation of quantum mechanics with the current Copenhagen interpretation believing that the phenomenon of probability exists within the superposition state. It was Edwin Schrödinger’s viewpoint that the wave and particle states in a quantum system somehow co-existed in the same space, despite the constraints of the laws of physics which explain that a wave state is an energy transport phenomenon and does not and cannot transport matter, and that the particle state is independent of the wave state. For example, when waves move through water, the water molecules do not travel in the wave but the wave moves through the water molecules. Similarly, when a billiard ball is pushed into a line of billiard balls, all the balls stay stationary except the last ball which moves. The same dynamic applies at the quantum scale.

No doubt this paper will cause much consternation amongst the followers of the Copenhagen

Interpretation of quantum physics, since it implies an annulment of the perspective of probability in the quantum state which is one of its fundamental precepts. Nonetheless, these words must be written and historical misperceptions need to be corrected, in order that the real nature of the quantum superposition state is correctly apprehended and accurately defined, and future research is based on coherent fundamental principles. The essential aim of science is to understand how phenomena operate in reality, so it is not advisable to invent a state such as the probability amplitude in the superposition state that does not actually exist in real terms. Edwin Schrödinger and Max Born based most of their work on the existence of probability amplitude and did not believe in the reality of the hidden variables theory which this article elucidates. Each of these physicists believed in the existence of a particle state before observation (giving rise to the vexed question of whether or not Schrödinger’s cat is dead or alive!) and did not comprehend the fact that the superposition state is purely informational and therefore contains neither a wave nor a particle state and therefore no cats in existence whatsoever. This false assumption on their behalf, has led to a series of further complicated misperceptions including the many worlds theory and multiple universes. This web of misunderstanding created by the belief in a probability wave has itself led to more and more complicated understandings of the quantum state. Nature is simple. Quantum mechanics is also. It is simple in its dynamics and form. Quantum physics must return to its simplistic roots in order to advance.

For those physicists who are brave enough to swim upstream against the strong undertow of the consensus opinion regarding the Copenhagen interpretation of quantum mechanics to reach the pure, clear waters of the reality of hidden variables, will find a far more fertile soil in which to further their research into the subtleties of the quantum state. For it has been admitted by eminent physicists [8] that the Schrödinger equation does not predict the reality of a single particle state existing at a local level, but rather its mathematical elegance predicts a state where two particles exist in different locations simultaneously, which has never actually been observed and will never be observed, since it is a false notion that a single particle can exist simultaneously in two discrete spaces.

It is my heartfelt wish that this paper will be given serious consideration and review in scientific academic and research circles. The unanswered questions that have lingered for ninety-four years, ever since the completion of the 5^th Solvay Conference in Belgium in 1927 regarding the true definition of a wave function, the lack of clarity regarding the existence of either the probability amplitude or hidden variable states and the concept of wave-particle duality need to be settled once and for all, in order that previous inconsistencies can be ironed out and the necessary corrections made so we can move forward coherently. These corrections include the realistic definition of the wave function as being the information of the quantum superposition state of the states of spin and total angular momentum. These two states hold within themselves the eight hidden variables pertaining to the formation of the wave and particle states that occurs upon observation and subsequent collapse of the superposition state. It is the information of these eight hidden variables that determine the type and properties of the kinetic wave and inertial particle states. This is quantum determinism. As Albert Einstein so famously said “God does not play dice”. This paper finally gives credence to this statement and explains why the perspective of indeterminism within the quantum state is incorrect. This deterministic theory of hidden variables within both m_s and m_l of the superposition state (a.k.a. wave function) presented herein, facilitates a coherent and realistic model of how the quantum states of wave and particle arise that mirrors the observable evidence within actual quantum research. The fact that for over eighty years – no probability wave has ever been discovered gives further leverage to the concept of quantum determinism discussed herein.

The dilemma of whether the quantum state is based on uncertainty (indeterminism) or certainty (hidden variables–determinism) is at the heart of the schism of thought in quantum physics. In order to move quantum research forward, we need to gain a unified perspective regarding the true nature of the quantum superposition state and a generally agreed definition of the term “wave function”. Once we have reached agreement on these fundamental principles, we can then move forward with clarity, accuracy and inspiration.

The material universe operates under the auspices of the three unitary symmetry groups of the Standard Model of Physics. These three unitary matrices underpin all dynamic and inertial states in the quantum realm. There is an implicate order to the cosmos [9]. The cosmos does indeed contain randomness, chaos and entropy but these states themselves emerge from a highly ordered state of coherent symmetry. Just as information theory arises from the states of nought and one, so too does quantum field theory emerge from the states of m_s and m_s. it is from this informational dual space of the unobserved quantum superposition state that, upon observation, the discrete states of the wave and particle emerge. Order precedes disorder and determinism is embedded in the superposition state which is the wave function itself.

For the sake of our future generations, may we begin to work together to implement this revised definition of the quantum wave function, so that our quantum research can rapidly advance in ways that are sustainable and creative as well as benefitting all living beings on our beautiful planet.

References

1. Wave function Properties.
2. Munns Christina (2013) Principia Unitas – Vol. II – The Quantum Mechanism
3. Orbirtal angular momentum of light. Wikipedia. 
4. Spin angular momentum of light. Wikipedia. 
5. Chrapkiewicz, Radosław., Jachura, Michał., Banaszek, Konrad., Wasilewsk, Wojciech (2016) Paper: “Hologram of a Single Photon”, Faculty of Physics, University of Warsaw.
6. Vibrations and Waves - Lesson 1 - The Nature of a Wave.
7. Electron beam, physics. As from a betatron.
8. Greene, Brian, World Science Festival video - Quantum Reality: Space, Time, and Entanglement.
9. Bohm, David (1980) Wholeness and the Implicate Order, Routledge Classics.