The problem of proper quantum theory of the gravitational field, and thus understanding what is quantum spacetime, is still open and is discussed here.
So, we introduce here the term of CES to replace the erroneous term of “black hole”, since there can’t be a hole per se in the fabric of matter that exists in gaseous, liquid and solid states in spacetime continuum.
Accordingly, we attempt here to merge the loop quantum gravity (LQG) with quantum mechanics and general relativity, for per Einstein, gravity is not a force – it is a property of spacetime itself.
Hence, our CES loop quantum spring model (ill. 1) fits said property of spacetime and is based on our previously published unified theory and model where we apply the string theory to loop quantum gravity by showing that a CES (formerly termed a “black hole”) is created by gravitational coupling of two linear superstrings in specified boundaries of open strings which are segments with endpoints, and closed strings which form closed loops. (Ill. 1)

Ill. 1 Loop Quantum Spring Image
Common research of black holes is based on simple notion of singularity and star's gravitational collapse to form black hole. Our comprehensive research shows that that cosmic energy system is not a hole per se, since it acts as matter accumulator, energy saver and gravitational accelerator of particles which is formed in duality of superstrings in loop quantum gravity of unified quantum field.
Research Fundamentals
It is assumed that “black hole” is formed when star core collapses under hugely amplified magnetic field. But per duality and energy conservation principles, the deformed matter contains the remnants of accumulated energy to be transformed and transferred from one form to another per energy conservation law and Hamilton principle which is valid for particles or deformable bodies, where Einstein–Hilbert action is applicable.
We had previously shown in our paper of unified matter theory that spacematter under said conditions would consist of two parallel superstrings in supertension under gravity that are coupled in a loop quantum field system.
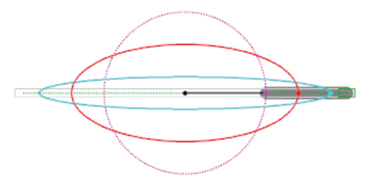
Accordingly, the dynamics of said physical system (CES) under strongly amplified magnetic field is configured in our model to two coupled superstrings of matter, forming an elliptical energy structure, integrating loop quantum spring at the left section of that structure. (Figure 1, Figure 2)

Figure 1. Cosmic Energy System of Coupled Superstrings

Figure 2. Loop Quantum Spring
On macro scale, the CES, formerly considered as black hole, is a cosmic superstructure, consisting of a central ellipsoid (pictured in ultramarine) with a jet of plasma from its center, encapsulated by corona ellipse (red) within a sphere (violet) of elliptical boundaries and orbits of matter as in ill. 2 and 3 below.
Figure 3.1 - mid-plane section of a supersonic jet breaking through an inhomogeneous disk of dense gas in the core region of a radio galaxy (Sutherland & Bicknell). This 512^3 simulation was done on the APAC AC supercomputer.
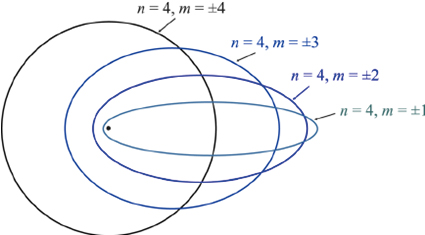
Said CES model is confirmed by quantum mechanics and the Bohr-Sommerfeld atomic model (ill. 4, below) where Sommerfeld-Wilson quantisation conditions arise naturally.
Ill. 2

Ill. 3
Ill. 4
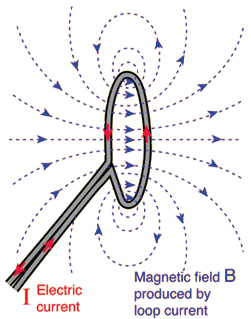
Ill. 5
This shows the connection between the complex 3 dimensional matter spin texture due to shape deformation and the spin transport properties as in our CES model with its geometry and entanglement entropy of surfaces in loop quantum gravity within embedded spatial surfaces.
Hence, our CES model represents the transition of a trapped region in a closed superstrings ellipsoid (fig.1, above) to superstrings’ anti–trapped region released by rotating loop quantum spring (fig. 2 above) that triggered a jet of matter in quantum geometry transition akin to gravitational tunneling.
Definition
The discussed above elliptical CES acts as cosmic energy accumulating, saving and accelerating system to secure the equilibrium of the galaxies that integrate such CESs.
Said elliptical CES releases its loop quantum spring under internal plasma pressure compressed by the hugely amplified magnetic field (see similar simple process on earth (ill 5).
by activating its loop quantum spring at the left to open the CES to eject a jet of matter generated by the motion of conductive plasma inside magnetic field. This is due to the excess energy of electromagnetic quanta, as singular jet of plasma in our CES model, without plasma recoil as shown erroneously in artists’ black hole rendition.
(For quantum spring see ref: 1, 2), for Loop Quantum Gravity and String Theory via Quantum Geometry see ref. 3, 4, 5. On elliptic quantum groups and matter coupling see ref, 6, 7 all below)
We unite here String Theory with Loop Quantum Gravity, since our elliptical CES model with loop quantum spring fits the elliptic analogue of multiple zeta values in one-loop supertring amplitude in open string theory.
Polylogarithms, Multiple Zeta Values and Superstring Amplitudes
Johannes Broedel, Oliver Schlotterer, Stephan Stieberger
17 Dec. 2014, arXiv. 1412.5535, revised 15 April, 2017
Some Developments of the Casimir Effect in p -Cavity of (D+1) -Dimensional Spacetime
Authors: Xiang-Hua Zhai, Rui-Hui Lin, Chao-Jun Feng, Xin-Zhou Li Journal-ref: Int. J. Mod. Phys. A29(2014)1430068
In this paper, we will give a short review on textit{quantum spring}, which is a Casimir effect from the helix boundary condition that proposed in our earlier works. The Casimir force parallel to the axis of the helix behaves very much like the force on a spring that obeys the Hooke's law when the ratio r of the pitch to the circumference of the helix is small, but in this case, the force comes from a quantum effect, so we would like to call it \textit{quantum spring}. On the other hand, the force perpendicular to the axis decreases monotonically with the increasing of the ratio r . Both forces are attractive and their behaviors are the same in two and three dimensions.
Alexander Yefremov. Peoples' Friendship University of Russia
Compact derivation of mathematical equations similar to those of quantum and classical mechanics is given on the base of fractal decomposition of a three-dimensional space. In physical units the equations become Shrödinger and Hamilton-Jacobi equations, the wave function of a free particle associated with a virtual ring. Locally uniform motion of the ring in the physical space provides an original helix (or regular cylindrical spring) model of a relativistic theory equivalent in results with special relativity, the free particle's relativistic Lagrangian emerging automatically. Irregular spring model generates theory similar to general relativity. (Figure 3)
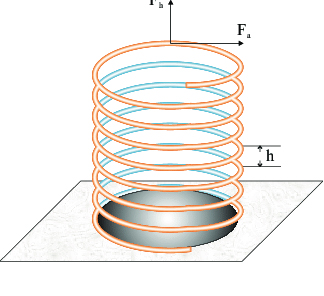
Figure 3. Cylindrical Spring
Connecting Loop Quantum Gravity and String Theory via Quantum Geometry
D. Vaid, Department of Physics, National Institute of Technology Karnataka (NITK), India
dvaid79@gmail.com
January 9, 2018
We argue that String Theory and Loop Quantum Gravity can be thought of as describing different regimes of a single unifed theory of quantum gravity. LQG can be thought of as providing the pre-geometric exoskeleton out of which macroscopic geometry emerges and String Theory then becomes the effective theory which describes the dynamics of that exoskeleton. The core of the argument rests on the claim that the Nambu-Goto action of String Theory can be viewed as the expectation value of the LQG area operator evaluated on the string worldsheet. A concrete result is that the string tension of String Theory and the Barbero-Immirzi parameter of LQG turn out to be proportional to each other.
Geometry Transition in Covariant Loop Quantum Gravity
Marios Christodoulou
Centre National de la Recherche Scientifique,
Centre de Physique Théorique Aix-Marseille Université,
Case 907, F-13288 Marseille, France
Full text: (Received 11 September 2018, accepted 23 October 2018)
In this manuscript we present a calculation from covariant Loop Quantum Gravity, of a physical observable in a non-perturbative quantum gravitational physical process. The process regards the transition of a trapped region to an anti–trapped region, treated as a quantum geometry transition akin to gravitational tunneling. The physical observable is the characteristic timescale in which the process takes place. Focus is given to the physically relevant four–dimensional Lorentzian case.
We start with a top–to–bottom formal derivation of the ansatz defining the amplitudes for covariant Loop Quantum Gravity, starting from the Hilbert-Einstein action. We then take the bottom–to–top path, starting from the Engle-Perreira-Rovelli-Livine ansatz, to the sum–over–geometries path integral emerging in the semi-classical limit, and discuss its close relation to the naive path integral over the Regge action. We proceed to the construction of wave–packets describing quantum spacelike three-geometries that include a notion of embedding, starting from a continuous hypersurface embedded in a Lorentzian spacetime.
We derive a simple estimation for physical transition amplitudes describing geometry transition and show that a probabilistic description for such phenomena emerges, with the probability of the phenomena to take place being in general non-vanishing. The Haggard-Rovelli (HR) spacetime, modelling the spacetime surrounding the ge- ometry transition region for a black to white hole process, is presented and discussed.
We give the HR-metric in a form that emphasizes the role of the bounce time as a spacetime parameter and we give an alternative path for its construction. We de- fine the classical and quantum observables relevant to the process, propose an interpretation for the transition amplitudes and formulate the problem such that a path integral over quantum geometries procedure can be naturally applied.
We proceed to derive an explicit, analytically well-defined and finite expression for transition amplitude describing this process. We then use the semi–classical approximation to estimate the amplitudes describing the process for an arbitrary choice of boundary conditions. We conclude that the process is predicted to be allowed by LQG, with a crossing time that is linear in the mass. The probability for the process to take place is suppressed but non-zero. We close by discussing the physical interpretation of our results and further directions.
Many theories of quantum gravity, as string theory, loop quantum gravity, and doubly special relativity, predict the existence of a minimal length scale and outline the need to generalize the uncertainty principle. This generalized uncertainty principle relies on modified commutation relations that – if applied to the second quantization – imply an excess energy of the electromagnetic quanta as singular jet of plasma.
Geometry and Entanglement Entropy of Surfaces in Loop Quantum Gravity
David Grüber, Hanno Sahlmann, and Thomas Zilker
Phys. Rev. D 98, 066009 – Published 18 September 2018
In loop quantum gravity, the area element of embedded spatial surfaces is given by a well-defined operator. We further characterize the quantized geometry of such surfaces by proposing definitions for operators quantizing scalar curvature and mean curvature. By investigating their properties, we shed light on the nature of the geometry of surfaces in loop quantum gravity. We also investigate the entanglement entropy across surfaces in the case where spin network edges are running within the surface. We observe that, on a certain class of states, the entropy gradient across a surface is proportional to the mean curvature. In particular, the entanglement entropy is constant for small deformations of a minimal surface in this case. (Figure 4)
Figure 4.
Communications in Mathematical Physics
December 1996, Volume 181, Issue 3, pp 741–761 | Cite as
On representations of the elliptic quantum group Eτ,η(sl2)
- Authors
- Authors and affiliations
- Giovanni Felder
- Alexander Varchenko
- Giovanni Felder
- Alexander Varchenko
- 1.Department of MathematicsUniversity of North Carolina at Chapel HillChapel Hill, USA
We describe representation theory of the elliptic quantum groupEτ,η(sl2). It turns out that the representation theory is parallel to the representation theory of the YangianY(sl2) and the quantum loop group U q (sl ˜ 2 ) Uq(sl~2) .
We introduce basic notions of representation theory of the elliptic quantum group Eτ,η(sl2) and construct three families of modules: evaluation modules, cyclic modules, one-dimensional modules. We show that under certain conditions any irreducible highest weight module of finite type is isomorphic to a tensor product of evaluation modules and a one-dimensional module. We describe fusion of finite dimensional evaluation modules.
In particular, we show that under certain conditions the tensor product of two evaluation modules becomes reducible and contains an evaluation module, in this case the imbedding of the evaluation module into the tensor product is given in terms of elliptic binomial coefficients. We describe the determinant element of the elliptic quantum group. Representation theory becomes special ifNη=m+lτ, whereN,m,l are integers. We indicate some new features in this case.
Elliptic Quantum Groups and their Finite-Dimensional Representations
Authors: Sachin Gautam, Valerio Toledano-Laredo
(Submitted on 20 Jul 2017 (v1), last revised 26 Feb 2019 (this version, v2))
Let g be a complex semisimple Lie algebra, tau a point in the upper half-plane, and h a complex deformation parameter such that the image of h in the elliptic curve E_tau is of infinite order. In this paper, we give an intrinsic definition of the category of finite-dimensional representations of the elliptic quantum group E_{h,tau}(g) associated to g. The definition is given in terms of Drinfeld half-currents and extends that given by Enriquez-Felder for g=sl_2. When g=sl_n, it reproduces Felder's RLL definition via the Gauss decomposition obtained by Enriquez-Felder for n=2 and by the first author for n greater than 2.
We classify the irreducible representations of E_{h,tau} in terms of elliptic Drinfeld polynomials, in close analogy to the case of the Yangian Y_h(g) and quantum loop algebra U_q(Lg) of g. A crucial ingredient in the classification, which circumvents the fact that E_{h,tau} does not appear to admit Verma modules, is a functor from finite-dimensional representations of U_q(Lg) to those of E_{h,tau} which is an elliptic analogue of the monodromy functor constructed in our previous work arXiv:1310.7318. Our classification is new even for g=sl_2, and holds more generally when g is a symmetrisable Kac-Moody algebra, provided finite-dimensionality is replaced by an integrability and category O condition.
Matter coupling
Kaluza-Klein approach seems to be able to go somewhere. Supergravity theory fixes the space-time dimensionality to be eleven and at the same time provides the matter fields necessary for compactification to four dimensions. There we also work in an Einstein-Cartan space-time because of the spinor fields, but the geometrization proposal is very different from the one presented here, besides taking quantum effects into account So geometrization of the fundamental interactions may still survive. Ref. 1
The Einstein-Cartan geometry is the most general geometry that preserves l ength under para1 lel transportl '6. There are two bas ic quantities: the space-time metric and the connection From the connection we can build two tensors, the Riemann curvature tensor and the torsion tensor (ref. 2, 3):
 (A.1)
(A.1)
 (A.2)
(A.2)
- Salam A, Strathdee J (1982) On Kaluza-Klein theory. Ann Phys 141: 316- 352. [crossref]
- Fonseca Neto Da Jb, Rivelles Vo (1986) A Geometric Formulation of Einstein-Maxwell Theory in Einstein-Cartan Space-Time . Revista Brasileira de Flsica 16: 4. [crossref]
- Heh, P. von der Heyde FW, Ketlick GD, Mester (1976) General relativity with spin and torsion: Foundations and prospects. Rev Mod Phys 48: 393. [crossref]
- Rovelli C, Smolin L (1987) A new approach to quantum gravity based on loop variables.
- Pullin J (1994) Knot theory and quantum gravity in loop Space: A Primer AIP Conf. [crossref]
- Ashtekar A, Corichi A, Zapata J A (1998) Quantum theory of geometry. Class.Quant.Grav. [crossref]










 (A.1)
(A.1)