The beautiful Titius-Bode law about Solar planetary orbits discovered in 1766, is considered that it is a mathematical coincidence rather than an "exact" law, because it has not yet been physically proved. However, if the disturbance restoration and the stability of the asteroid belt orbit are considered, there must be some underlying logical necessity.
Planetary orbits are often computed by Newtonian mechanics with the kinetic energy and the universal gravitation energy. Nevertheless, if the principle of energy-minimum is applied to the Newtonian mechanics of orbits, it is reduced to the result that the stable orbital radius is only one value, which is totally incompatible with actual phenomena. This discrepancy must be resulted from the shortage of elements which rule over the planetary orbits. Other elements to rule over the planetary orbits must be the electric charge energy and the rotation energy, both of which are guided by the Kerr-Newman solution (discovered in 1965) of the general relativity theory (discovered in 1915). Here, the Titius-Bode law was mathematically demonstrated and also the number maximum 31 of Saturn’s rings and the radius of the Fine-Ring were calculated for the first time by means of applying the principle of energy-minimum to the complicated energy equation which adopts Kerr-Newman’s mass, electric charge and rotation elements of the central core star and solving the sole differential equation. It is expected that fundamental three element constants of the Sun and the Saturn will be decided in the future.
Titius–Bode law; Saturn’s rings number; fine ring; energy stable orbits; Kerr-Newman solution.
The Titius–Bode law discovered 250 years ago, is considered that it is a mathematical coincidence rather than an "exact" law [1], because it has not yet been physically proved. However, if the disturbance restoration and the stability of the asteroid belt orbit are considered, there must be some underlying logical necessity. Here, by energy methods using the Kerr-Newman solution of the general relativity theory, the Titius-Bode law was demonstrated and its solution method was applied to the calculation of the number of Saturn’s rings and the radius of Fine-Ring. This paper is a mainly mathematical calculations and the memos of detailed analysis processes are in a separate of paper [2].
The outline of the solution method and the key equation numbers in the paper are shown as follows.
1) The equation for energy in the space-time field is obtained from the Kerr-Newman solution, a strict solution of the Einstein equations of the general relativity theory.
f 1(ρ, θ, dρ/dt, dθ/dt, dφ/dt, ε) = 0 (eq. 3）
2) This energy equation is partially differentiated by θ to the minimum energy. The result is θ=π/2, and the calculation below proceeds at θ=π/2, i.e., on the equatorial plane.
f 2(ρ, π/2, dρ/dt, 0, dφ/dt, ε) = 0
3) The angular momentum equivalent J is obtained by applying the variational principle to the Kerr- Newman solution to calculate dφ/dt .
ξ(ρ, dφ/dt, J) = 0 (eq. 6)
4) Because an additional radius is dρ＝0 at the aphelion and perihelion distances R, the calculation below proceeds at distance R.
f 3(R, π/2, 0, 0, dφ/dt, ε) = 0 (eq. 7)
5) Substituting dφ/dt from ξ = 0 into f 3 = 0 results in a relational expression of the radius, the angular momentum equivalent, and the energy.
f 4(R, π/2, 0, 0, J, ε) = 0 (eq. 9)
6) The orbital distance R is determined by the energy and the angular momentum equivalent, i.e., R = R(ε,J). R is partially differentiated by ε , that is, f 4 is partially differentiated by ε.
g (R, J, ε, ) = 0 (eq. 10)
7) Derive the angular momentum equivalent J from f 4(R, π/2, 0, 0, J ,ε) = 0 and substitute it into g (R, J, ε, ) = 0. Make this into an important differential equation which is just composed of the radius and the energy to analyze unique characteristics of orbits.
h(R, ε, dε/dR) = 0 (eq. 11)
8) Solving the differential equation h results in a complicated set of arctan, log, power functions and an integration constant K.
H(R, ε, K) = 0 (eq. 14) (eq. 15)
9) By using that the minimum energy is dε/dR=0 in h(R, ε, dε/dR) =0, following simultaneous equations are obtained and solved.
h(r, εmin , 0) = 0 ① H(r, εmin , K) = 0 ② (eq. 16)
10) Because the integration constant K is common to all orbits, the Titius–Bode law is demonstrated and also the number of Saturn’s rings and the radius of Fine-Ring are calculated.
I (r, K) = 0 (eq. 23) (eq. 26) (eq. 27)
Introduction to the Energy Equation
There are two preconditions for the following analysis besides it in the Kerr-Newman solution.
1) The analysis object must be sufficiently far from the center of mass.
2) The rotation speed of the center of mass must not be too fast. The characteristic Boyer-Lindquist coordinates in the Kerr solution are equal to general polar coordinates in the first-order term [3].
The strict Boyer-Lindquist metric of the Kerr-Newman geometry [4], the postulational no-hair theorem can be summarized as follows. These characters as ds2, R2Δ, dt are implied Boyer-Lindquist symbols.
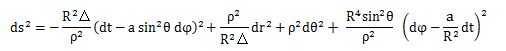
At the large radius r, the Boyer-Lindquist metric can be shown as follows.
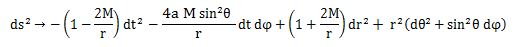
Symbols are changed from the Boyer-Lindquist metric to the general polar coordinate.
The Kerr-Newman solution of the general relativity theory is given by (eq.1). In this expression, and e are the mass, rotation and electric charge elements respectively.
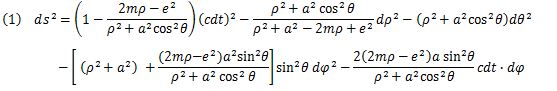
Γ can be shown as follows when ds is divided by the time elements (c dt).
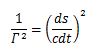
The Lorentz transformation factor γ (= c dt/ds) in the Minkowski space-time of the special relativity theory is an important component of the energy E = M c2 = M0 γ c2 . Γ (= c dt/ds) of the Kerr-Newman solution of the general relativity theory is analogous to γ.
On this occasion, by following the principle of minimum energy, the sign of m is changed to –m, a is changed to +a, and e is changed to +e. Therefore, the energy equation is Ｅ＝Γ ( ρ, θ, φ, t, –m, a, e).
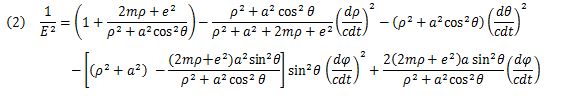
Since E has a decisive massive energy M0c 2, it is converted into ε in (eq.3).
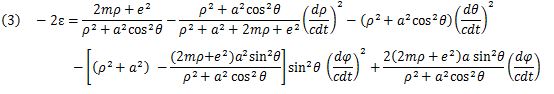
Partial differentiation is used to minimize the energy ε (ρ, θ, φ, t) by using ∂ε/∂θ = 0.
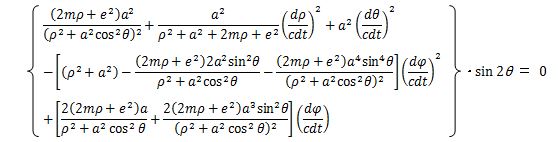
That is, the energy E and ε are minimized at θ=π/2 and the planets gather on the equatorial plane where the energy is stable if the center of mass has rotation.
Time component from the variational principle
When the rotation speed of the center of mass is not too fast, the Kerr-Newman solution expanded in the first order of α/ρ takes the form given in (eq.4):
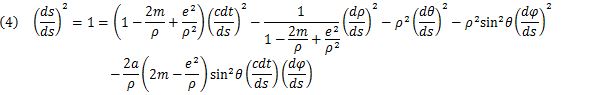
The Euler–Lagrange equation [5] is adopted by applying the variational principle to the Kerr-Newman solution.
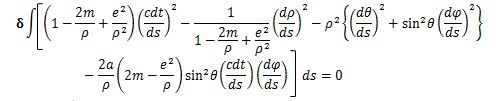
Eventually, (eq.5) is obtained at the equatorial plane of the rotating center of mass where the energy is stable. Hereafter, the calculation is performed at the equatorial plane (θ＝π/2) of the rotating center of mass.
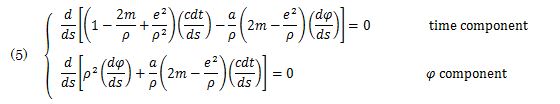
The two equations in (eq.5) are integrated over ds. (eq. 6) with an integration variable J is obtained by using the resulting pair of simultaneous equations,
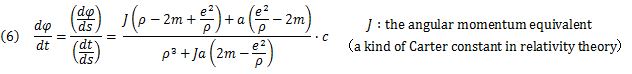
The distance variables are defined as follows:
ρ：An arbitrary orbital distance in two- or three-dimensional coordinates.
R：The aphelion and perihelion distances at the equatorial plane of the rotating center of mass.
r：The aphelion and perihelion distances, both of which are energetically stable at the equatorial plane.
Introduction of the angular momentum equivalent
Since additional ρ at the aphelion and perihelion distances is dρ＝0, the energy equation is given by (eq.7).
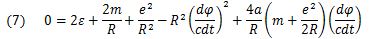
dφ/cdt (eq. 6) is composed of the angular momentum equivalent and is substituted into (eq.7). J is obtained as in (eq.8) by adopting the secondary order R.
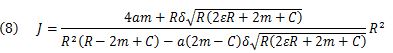
Here, δ = ±1 and C = e2/R. δ is related to the orbital rotation direction.
Introducti on of the Space Fantasy differential equation
It leads not to the numerical analysis but to the analytical unique characteristics. The relation of R , ε, and J are given as (eq.9) at the aphelion and perihelion distances R by changing the angular momentum equivalent J (eq. 8).
(eq.9) is far more complicated than the Kepler-Newton equation 2εR2 + 2mR – J2 = 0
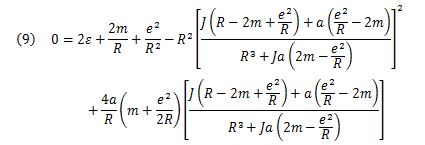
Since the orbital distance R is determined by the energy ε and the angular momentum equivalent J, it is R = R(ε,J). A new differential equation is given as (eq.10) by partially differentiating R by ε, then substituting J into this, and adopting the reciprocal of ∂R/ ∂ ε. It can be shown as follows.
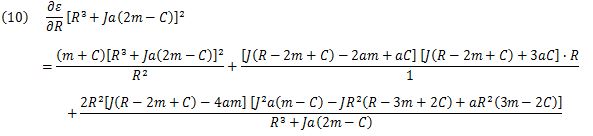
Here, by substituting J of (eq. 8) into (eq.10), the second order R is obtained.
Through all these extensive calculation processes, the relation between ε and R is summarized as (eq.11).
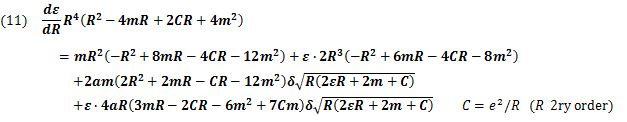
The second order equation (eq. 11) is called tentatively “the Space Fantasy (SF) differential equation”.
The change of variables is performed to solve the SF differential equation for S. The result is (eq.12).
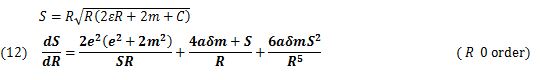
The form of the differential equation in (eq.12) is more complicated than the Riccati's differential equation, which never has an exact general solution [6]. Since 6αδmS2/ R5 is much smaller than S/R and 4αδm/R, it can be treated as a constant θ. Also, (eq.12) can be reduced to the problem of an approximate differential equation, and it is given as (eq.13).
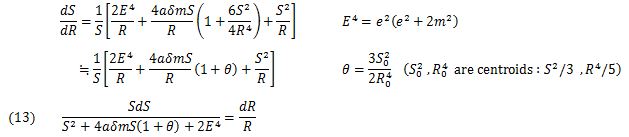
Solving (eq.13) by the quadrature formulae [7] leads to (eq.14), (eq.15) and (eq.16).
Without use of the SF differential equation which leads the analysis solution, there is a method of numerical solution i.e. simultaneous equations consist of an integral constant equation and an energy minimum orbit equation. However, a numerical solution composed of power algebraic expressions is difficult to understand the characteristics of orbits.
In the case that the discriminant is Δ = E4 — 2α2m2(1+0)2 > 0:
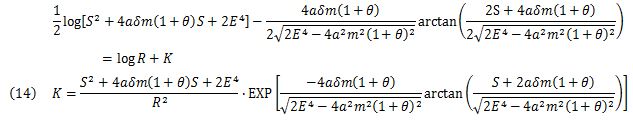
In the case that the discriminant is ΔE4 — 2α2m2(1+0)2 < 0:
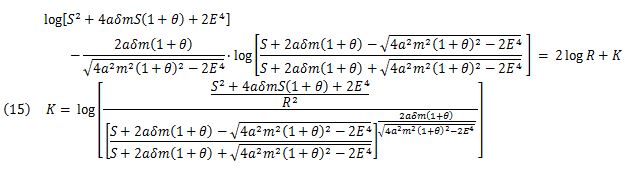
In the case that the discriminant is ΔE4 — 2α2m2(1+0)2 < 0:
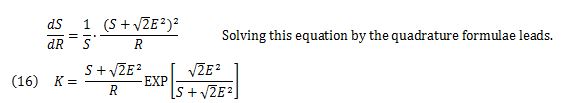
Conditions of the energy minimum orbit
Since the minimum energy is dε/dR = 0 in the SF differential equation (eq. 11), it is a cubic equation in ε.
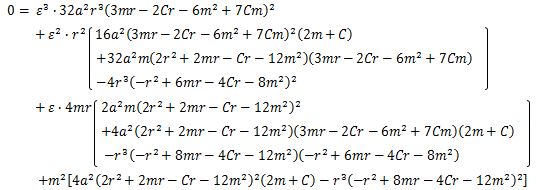
Solving this cubic equation can be shown as follows. A solution εmin (eq.17) very close to 0 is adopted in accordance with the principle of the energy minimum.
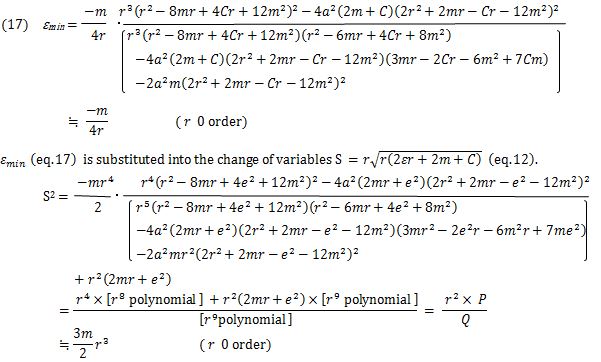
Here, P and Q are given by (eq.18) and (eq.19).
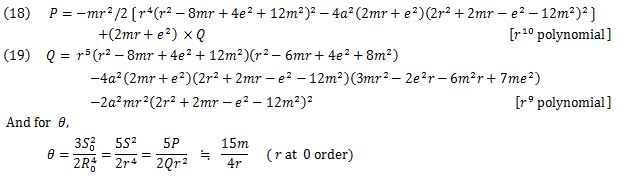
In the case that the discriminant is Δ = E4 — 2α2m2(1+0)2 > 0 of the SF differential equation, the function ƒ(θ) is given in (eq.14) and is subjected to a Maclaurin series expansion. Terms above θ2 are neglected. The result is given in (eq.20).
Since the integration constant K is common to all planets that orbit the center of mass, the base planet and the distance ratio to the base planet can be set as follows. r1 , N1 , N－N1＝ , and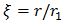 
. The result is given in (eq.21).
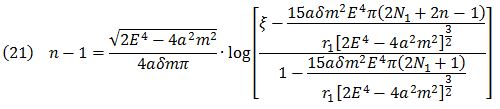
On the other hand, the Titius-Bode law is changed into (eq.22).
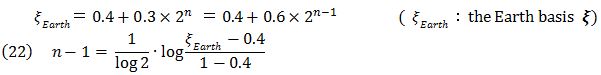
The Titius-Bode law (eq. 22) is remarkably similar to the solution (eq. 21) of the approximate SF differential equation. If the two coefficients are the same, the two equations are almost equal.
(The Earth is the base planet, n=1.)
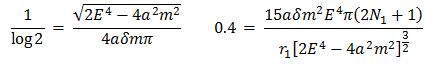
Since ϒ1 = 1.5 x 108 Km for the Earth, and, m = 1.476Km and α= 0.32Km [8] for the Sun it is calculated that e = 2.1km, and N1 = 1.5 × 107. The 2n on the right side of (eq.21) is neglected because of the very large N1 . Thus,
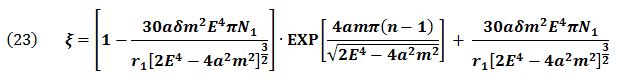
δ = ± 1 is related to the orbital rotation direction.
If the rotation direction of orbits is same that of the central core star, ± = + 1 and (Eq.23) is now exactly equal to (eq.22). The Titius-Bode law has therefore been demonstrated.
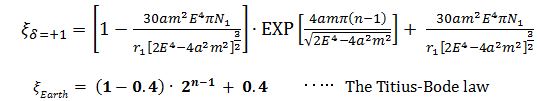
It is confirmed that there are around 4000 extrasolar planet systems and a few their orbits are observed.
The orbits with counter rotation direction against the fixed star
In the case that δ = - 1 i.e. the rotation direction of orbits and it of the fixed star are opposite each other, the ratio of orbital radii in some exoplanets is reversed against the solar system planets. [9]
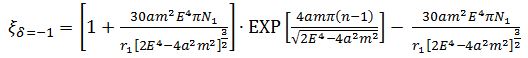
If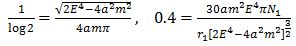 
like as the solar system planets, then 
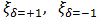and 
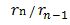are shown in the table1. n is larger and larger, 
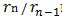nears 2.0 in both 
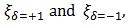, but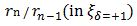 
is a monotonous increase 1.4 < 2.0 , 
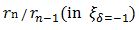is a monotonous decrease 3.3 > 2.0 at n=1. As a result, there are a few planetary systems with counter rotation direction against the fixed star really in the universe physically.
Table 1. the ratio of orbital radii 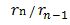and n
ｎ |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
ξδ=＋1, (1-0.4).2n-1 + 0.4 |
0.4 |
0.5 |
0.6 |
0.7 |
1.0 |
1.6 |
2.8 |
5.2 |
10 |
20 |
39 |
77 |
rn / rn-1 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
1.6 |
1.8 |
1.9 |
1.9 |
2.0 |
2.0 |
2.0 |
ξδ=―１, (1+0.4).2n-1 ― 0.4 |
-0.3 |
-0.2 |
-0.1 |
0.3 |
1.0 |
2.4 |
5.2 |
11 |
22 |
44 |
89 |
179 |
rn / rn-1 |
0.9 |
0.7 |
0.5 |
-0.3 |
3.3 |
2.4 |
2.2 |
2.1 |
2.0 |
2.0 |
2.0 |
2.0 |
Since the autorotation of the Saturn is fast, the discriminant is Δ = E4 - 2a2m2 (1+0)2 >0. The solution (eq. 15) of the SF differential equation is as follows.
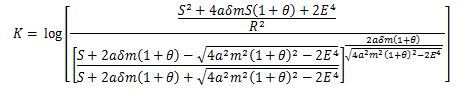
δ = ± 1 is related to the orbital rotation direction.
Since the power number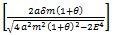 
is nearly 1, the denominator is expressed as ( 1 - λ). λ is extremely small, but not zero. The solution of the SF differential equation is (eq.24).
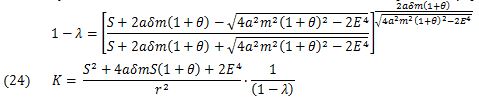
The integration constant K is common to all the rings that belong to the Saturn. For the base ring, the variables are r1 and F =K, and the polynomial of S can be shown as follows (eq.25).
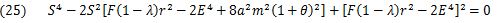
P (eq.18) and Q (eq.19) are substituted into (eq.25) to give S and 0. Finally, the polynomial of r can be shown as follows (eq.26).
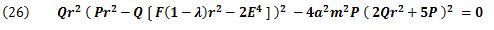
The degree of (eq.26) is the highest at the first term P2 Qϒ6, and is ϒ to the power of 35 (10x 2+9+6)．That is, (eq.26) is a polynomial of ϒ35 with high degree coefficient λ and has four micro roots. Thus, planets with rings such as the Saturn have a maximum of 31 rings. The real number of rings decreases because of roots of complex number, minus roots, equal roots and the swelling of the central core star.
Even by Cassini Spacecraft It is unable to determine the number of Saturn’s rings and expected to observe and determine the rotation element α and the electric charge element e .
The rings with counter rotation direction against the central core star
δ = ± is related to the orbital rotation direction. The coefficients λ and F contain δ.
In the case of δ = -1, there are a few ring stars having the rings with the counter rotation direction against the central core star each other really and they have a maximum of 31 rings.
(eq.24) changes as follow.
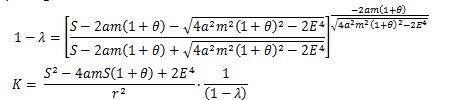
In the case that the discriminant is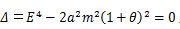 
since the balance of the mass, rotation and electric charge elements is exquisite,
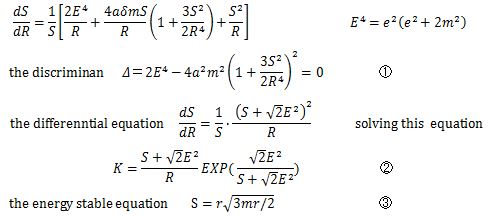
ϒ , S and K are unknown, then solve simultaneous equations ①, ② and ③
m , e and α are small constant values, but if it is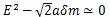 
generally, ϒ grows larger. That is, in the case of exquisite balance 
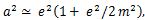, the Fine-Ring is formed such as Fine Ring nebura.
An astronomical long-standing task was solved at length not by the computer analysis but by the theoretical analysis. Today, since the computer capacity is highly advanced, many space scientists research the evolutional development from primitive spaces to near earth by computer simulations to calculate the Einstein’s equation and make good reports. However, here is the sole axisymmetric steady-state strict solution of the Einstein-Maxwell equations that is supported by “no-hair theorem and uniqueness theorem.”
The Kerr-Newman solution of the Einstein’s equation is considered as follows. According to the ref.[10],
the collapse leads to a black hole endowed with mass and charge and angular momentum but, so far as we can now judge, no other adjustable parameters: "a black hole has no hair," “no-hair theorem.”
The no-hair theorem postulates that axisymmetric steady-state all black hole solutions of the Einstein- Maxwell equations of gravitation and electromagnetism in general relativity can be completely characterized by only three externally observable classical parameters: mass, electric charge, and angular momentum in the Kerr-Newman solution:” uniqueness theorem.”
In this manner, since this paper is based on the steady state of Kerr-Newman solution in the mature galaxies, it cannot be applied to the galaxies which are still young, un-stable and transitional.
Three important equations of this paper can be summarized as follows.
(eq.11) is the fundamental differential equation based on the steady state, and it can be applied to the Solar system, other planets and rings in the galaxies. There must be many solutions of (eq.11).
(eq.23) is one of the approximate solutions of (eq.11). Since this is energetically stable, it is applicable to the Solar system planets and many of the around 4000 extrasolar planets in the galaxies. In the systems the arrangement of planets is a kind of geometrical series ξ= α Exp(bn)+c. However, it is not applicable to still young, un-stable and transitional planets such as comets.
Also (eq.26) is one of the approximate solutions. This is also energetically stable and applicable to Saturn’s rings and some other extrasolar planets’ rings. Planets with rings such as the Saturn have a maximum of 31 rings.
m, e and α are small constant values, but in the case of exquisite balances 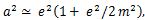the Fine Ring is formed (eq.27). The Fine Ring phenomena are occurred by the sole rotating central core star and by also resonances of some stars.
It is expected that fundamental three elements of the Sun, the Saturn and other stars will be decided in the future.
Acknowledgments
Funding: This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
I thank Dr. Yuko Masaki and Edanz Group (www.edanzediting.com/ac) for editing an early draft of this manuscript.
Author Contributions
F. I. created the idea, developed the theory and wrote the manuscript.
Competing Interests
The author declares no competing interests including financial and non-financial interests.
- Hans Merkl (2020) The Secret of the Titius Bode Law: A New Theory on How Our Planetary System Came Into Existence. Journal of Geography and Geology 11: 58.
- (2018) Internet A demonstration of the Titius Bode law and the number of Saturn’s rings by using the Kerr-Newman solution of the general relativity theory.
- Boyer R H., Lindquist R W (1967) Maximal analytic extension of the Kerr metric. Journal of Mathematical Physics 8: 265-281.
- Andrew J.S. Hamilton (2020) General Relativity, Black Holes and Cosmology. 207.
- Internet Euler Lagrange Differential Equation 2017.
- J. Liouville (1841) Journal de Mathematiques Pure et Appliquees Tome 6.
- Gerhard Merziger., Günter Mühlbach., Detlef Wille., Thomas Wirth (2013) Formeln+Hilfen Höhere Mathematik, (translated into Japanese).
- Edwin F. Taylor., John Archibald Wheeler (2000) Exploring Black Holes: Introduction to General Relativity. (p272, translated into Japanese by Nobuyoshi Makino).
- Winn., Fabrycky (2015) The Occurrence and Architecture of Exoplanetary Systems. Annual Review of Astronomy and Astrophysics 53: 409 2015.
- Markus Heusler (1996) Black Hole Uniqueness Theorems, Cambridge University Press.
