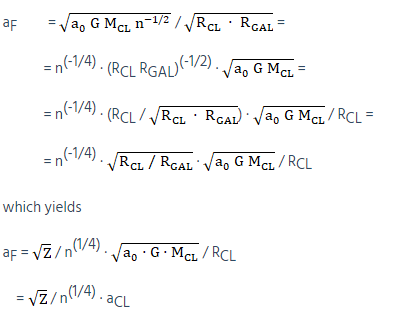One of the most effective theories to explain the discrepancies in gravitational potential in galaxies is Milgrom’s Modified Newtonian Dynamics (MOND). However, the modification of the laws of gravity cannot be justified on the basis of current fundamental physical theories, and some astrophysical observations do not match MOND’s predictions. Based on a modified interpretation of Einstein’s equation E=mc2, we propose a fluid spacetime-generating mechanism that might operate in nuclear reactions from active stellar bodies giving rise to additional spacetime curvatures, scale invariance and other essential predictions of MOND. The compliance of the conceptual model with observations in various astrophysical settings is discussed, as well as the consequences that it might imply for the problems of dark matter, dark energy and for our current understanding of black holes.
Dark matter is the longest standing problem in modern astrophysics. While several conjectural theories have been devised and are being actively researched, no current theory can explain the whole set of observed facts. Several authors have pointed out that some new physics might be needed. But new physics means no direct derivation from current foundational theories, unless some important observation has been overlooked or a logical mistake has been made, which seems unlikely, given the large community of highly committed and skilled scientists that have worked on the problem for decades. Most solutions proposed so far can be grouped as following one of two basic assumptions: Either (1) some amount of additional, unseen matter is present, or (2) the rules of gravity need to be modified.
But the dark matter problem can actually be viewed as a three-pronged problem, the third option being (3): Some additional source of spacetime curvature is acting to cause the observed anomalies (Fig 1) without any modification in the amount of mass nor change in the laws of gravity.

Figure 1: General Relativity (GR) describes spacetime curvature as a function of mass. Current theories of dark matter (DM) propose a modification of these laws or the presence of undetected matter to explain the observed discrepancies in curvature. A third option might be the existence of additional sources of spacetime curvature (Curv)
The most successful theory available today to explain the original anomalies in galaxy rotation curves is Milgrom’s Modified Newtonian Dynamics (MOND) [1-4] which posits a modified law of gravity based on a fixed cosmological acceleration scale. It postulates scale invariance for galaxies and succeeds in explaining the observed discrepancies in mass and gravitational fields. It correctly predicts flat galaxy rotation curves and the Tully-Fischer relation without any free parameters.
Unfortunately, MOND in its current form does not explain the gravitational fields observed in galaxy clusters, nor in colliding cluster pairs. More importantly, it does not provide a physical basis on which to base such a radical modification of well-proven laws of gravity and has therefore received subdued attention from the scientific community, in favor of the more intuitive particle dark matter hypothesis.
We shall focus here on the third option (Fig 1) and postulate an alternative source of spacetime curvature independent of the laws of gravity and based on a modified interpretation of the Special Relativity (SR) equation E = mc2. It will be argued that this should provide both a physical basis for MOND and a correction to its main shortcomings, i.e., the need to modify gravity and the discrepancies of MOND with the observations in galaxy clusters. Next, we shall make some predictions that would follow from the model and propose observational tests that could be used to validate or disprove it.
Plausibility of the Existence of Fluid Spacetime. Reinterpreting E = m c2
The formula E = γ m c2, likely the most famous in physics, states that a huge amount of energy is released from nuclear reactions that imply a net loss of mass. The formula is often taken to imply that mass and energy are the same thing, or two manifestations of the same thing but, strictly speaking, neither Special (SR) nor General Relativity (GR) explicitly demand that. What SR states is that there is a mathematical equivalence between mass and energy, not that they are the same thing.
The starting point for our argument is that in nuclear fusion reactions such as those taking place in stars, matter might transform into new spacetime with an output of energy that exactly amounts to mc2, in a way analogous to ordinary exothermal chemical reactions.
We stress the fact that SR’s equation E = mc2 need not be modified, but rather the underlying expression describing the events may be stated differently. This representation might be:
 (1)
(1)
in which we no longer have a mathematical equality, but arrows representing transformations, with E = mc2 describing the amount of energy released.
The process, if it actually exists, would be very hard to detect in the laboratory because of the huge amount of energy released at nuclear fusion reactions that completely dominates the resulting state of affairs. Furthermore, the amount of new spacetime generated per unit mass might be small and would intermingle perfectly with existing spacetime. The best chance of detecting it would likely be in astrophysical observations at galactic and cosmological scales, where gravity dominates and spacetime behavior is routinely analyzed.
The nature of the generated spacetime, as well as its precise amount (the constants λ and β above) are currently unknown. We can only speculate about some of the properties that could be expected and the consequences that would follow.
In support of the plausibility of such a reinterpretation, we quote from a contemporary physicist:
“It has been said by many physicists and philosophers that the formula E = m·c2 means that ‘mass is equivalent to energy’. This is philosophically false. It is not what Einstein said when he derived this relation. What he said was that “the inertial mass of matter is a measure of its energy content.” In physics, as Newton originally postulated, the inertial mass of matter is, by definition, a measure of its resistance to change its state of rest or constant motion. The energy of matter, on the other hand, is by definition, the capability of this matter to do work. Thus, mass and energy are totally different concepts!” [5].
Fluid Spacetime (FS). An Intuitive Basis Models
We propose the following thought experiment. Let us consider a typical spiral galaxy and assume that a certain amount of space (properly spacetime, as will be understood henceforth) is generated per unit time in all its stars in relation to their mass. Such spacetime would then distribute radially as a fluid with zero mass, zero viscosity, and a low time constant. Once generated, it mixes up with and adds to the existing spacetime, sharing its known properties described by GR, i.e., it curves and warps, is able to expand and gives rise to gravitational fields determined by local curvatures. The essential fact in this hypothetical Fluid Spacetime (FS) is that it behaves as a fluid, slowly spreading away from its source and by so doing displaces existing spacetime and results in a modification of local curvature. This could be visualized intuitively as a conventional viscous fluid poured on a flat surface slowly spreading away from its source. In contrast to conventional fluids, movement of spacetime would not follow a pressure or mass-density gradient, but a spacetime-density one, a concept that is hard to imagine and will remain for the time being undefined. We can only guess that, if the following conditions are met, changes in curvature arise that are relatively persistent as the fluid flows:
(i) New spacetime is generated at each star in proportion to its mass, and the amount per unit time is small compared to the existing spacetime.
(ii) The induced spacetime curvatures at short ranges are small compared to the curvatures generated from gravity, and
(iii) Spacetime fluid is endowed with some degree of plasticity, i.e., induced curvatures persist unless modified by gravity or by further changes in the flow of spacetime.
Otherwise the properties of fluid spacetime (FS) will be assumed to be consistent with the known properties of vacuum and with special relativity, i.e., it has zero mass density and there is a limit to its rate of change set at the speed of light c.
We shall from now on represent in 2D phenomena that actually take place in 3D. We do that for convenience and also because both representations can be easily switched over unambiguously. In the end, we are interested in the trajectories of point-like stellar bodies, which in 3-D under spherical symmetry means geodesics, that is, great circles.
Under spherical symmetry, classical curvature scales with the inverse of the radius (in Riemannian curvature, with the inverse of the radius squared). For bodies orbiting with circular paths at constant normalized speed, curvature is mathematically equivalent to the rate of change of the direction of the velocity vector, i.e., to centripetal acceleration. Unless otherwise stated, we will use the terms curvature and acceleration interchangeably.
We postulate a steady production of spacetime at each star of a spiral galaxy proportional to its mass. The assumption of constancy is realistic, as the mass of stars does not change significantly along most of its lifespan because the rate of mass consumption in nuclear reactions represents only a minute fraction of the total mass of the star. Moreover, for all we know, the energy output of stars is approximately proportional to their mass, and certainly within an order of magnitude of it.
If we imagine a galaxy with a number of stars of the order of 10n, with n between 9 and 12, we can model it as a huge conglomerate of stars, each located at a random position around the galactic center, generating new spacetime at a rate proportional to its mass and each contributing a negligible amount to the global spacetime production. The distribution of this new spacetime is directed towards the outer radius of the galaxy, since movement in the opposite direction is precluded by an equivalent number of stars on the opposite side from the center pushing out an equivalent amount of spacetime. (Fig 2)

Figure 2: Spacetime generation from all the star in a galaxy related to the star’s mass gives rise to an expansion of spacetime that distributes radially away from the center. From the high number of randomly distributed stars that contribute to it, the effect can be modelled as a linear function of radial distance and time. Stars need not suffer a deviation from their stable orbits (text)
If we represent a thin radial slice of such a galaxy with its numerous stars and the distribution of spacetime within it, we get something similar to Fig 2. A displacement of spacetime is caused which is directed away from the center and holds a linear relation with radial distance, because the effect of any single star is cumulative with the expansion due to all inner stars in the same radial slice. From the random location of a high number of stars, an approximately linear expansion of space results, which is proportional to the average rate of fluid spacetime generation per star. We thus get the transformation (x → λ x) (Fig 3)
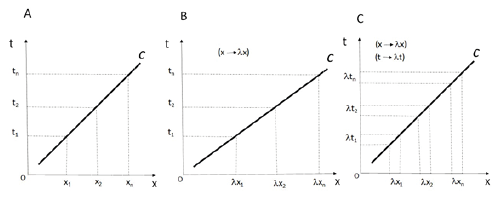
Figure 3: Linear expansion of space away from the galactic center would generate supraluminal velocities (A -> B) unless the expansion involves time as well (B -> C)
Time should likewise experience an equivalent dilation (t -> λt, Fig 3C), otherwise light speeds higher than c would result (Fig 2B), which is forbidden by Special Relativity. Such a transformation in spacetime shows radial symmetry and preserves geometrical figures. Curves in a plane (in 3D, a sphere) are expanded with their radius of curvature scaling as 1/R. (Fig 4, left). This in contrast to curvature due to gravity, which decays as 1/R2 (Fig 4, right).

Figure 4: Linear expansion of spacetime leads to preservation of curvature that scales as 1/r (left, red). Any preexisting spacetime curvature becomes ‘expanded’ by the generated new spacetime to λr with 1/λr curvature. Newtonian curvature would scale as 1/r2 (right, black)
The rate of spacetime expansion λ in the galaxy depends on the (constant) rate of spacetime generation per star and on the number of stars, which in turn depends on the mass of the galaxy. The total rate of spacetime generation can therefore be assumed to be constant in time. A star S on a circular orbit around the center of the galaxy and subject to the effect of such spacetime expansion would suffer no deviation from its orbit, because the slow and constant radial flow of spacetime away from the center is always directed perpendicular to the tangent of the orbit and to the velocity vector of the star (Fig 5). Spacetime flow would be viewed in the reference frame of the star as constant in speed and direction, i.e., by Galilean relativity would imply no acceleration. The star would remain on an orbit determined exclusively by the local curvature, i.e., it would feel only a centripetal acceleration equal to V2/R. In the case of elliptical orbits, the analysis would be more complicated, but the observed orbits of stars in spiral galaxies are largely circular, or with low eccentricity.

Figure 5: A star S on an orbit around galactic center O under the effect of fluid spacetime expansion would experience a centripetal acceleration as usual, equal to V2/R due to spacetime curvature. The star would remain unaffected by the the movement of spacetime, which would be seen from its reference frame as constant in direction and modulus. As proved by MOND, this leads to constant rotation velocities
The situation should be stable in time, with spacetime slowly flowing away from the galactic center while spherical symmetry and curvature are preserved.
We shall now examine the distribution of the generated curvatures as a function of radial distance, under the following assumptions:
(i) New spacetime is produced at every star in proportion to its mass, and both are constant in time.
(ii) The new spacetime induces a curvature that scales as 1/R. Because of the large number of stars that compose a galaxy, smoothness results. The individual contribution of any single star to the global curvature is negligible, i.e., there are no bumps or breaks. As will be discussed later, this condition might not apply in all situations.
(iii) The curvature generated by the FS mechanism at a distance R from the center is also proportional to the local rate of spacetime generated at that point, SPCTLOC.
(iv) With regards to the orbits of stars under spherical symmetry and constant speeds, acceleration and curvature scale linearly and can be considered equivalent.
From assumptions (i) and (ii), we try the following expression:
aF = K. M(α) / R (2)
being aF the acceleration due to the fluid-spacetime mechanism, R the radial distance from the center, and M the total galactic mass (strictly, the mass inside the R-sphere, but for fixed radius both masses are related and we can always assume our observations are carried out in the outer regions of the galaxy). We now find out the exponent α.
The rate of total spacetime generation for a sphere of radius R is constant and is related to the mass it contains (i).
SPCTGAL ~ M
With regards to the orbits of stars, galaxies do not expand with time because of their gravitational bond, and stars’ orbits do not change, as mentioned above. We can therefore treat the galactic geometry as fixed and need not concern ourselves with the expansion of the sphere due the increase in spacetime. Thus, the rate of local spacetime generation at a radial distance R from the center scales with the total rate of spacetime generated inside the R-sphere divided into the corresponding surface area, and therefore scales as 1/R2.
SPCTLOC = SPCTGAL / 4 π R2
SPCTLOC ~ 1/R2
Which means that to be able for make up for the inverse-square-law decay of local SPCT as a function of R, the amount of mass that is needed to produce a certain fixed rate of local SPCT at radius R scales with the radius squared. Since local spacetime generation and curvature scale (iii), the mass needed to generate a certain curvature at distance R also scales with R2.
M ~ R2 (for fixed local SPCT generation rate and curvature).
From this it can be already inferred that for equation (2) to hold, M should be raised to the exponent ½.
aF = K. 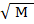 / R (3)
/ R (3)
We can check that this agrees with the observed baryonic Tully-Fisher relation in galaxies:
V4 ~ M
Equating the centripetal acceleration to our expression for fluid-spacetime acceleration (2):
V2 / R = K · M(α) / R
V2 = K. M(α)
But from Tully-Fischer, V4 scales as M, so that α = ½.
To determine now the value of K in equation (3) we need to use what MOND tells us about the observed galactic dynamics, where the effective acceleration is not the Newtonian aN, but rather
aMOND = 
where a0 is Milgrom’s experimentally measured universal constant acceleration. We have then
a0 = (aMOND)2 / aN = (K2 · M / R2) / (G · M / R2)
which simplifies to
a0 = K2 / G
K = 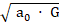
Inserting this into equation (3), we have an expression for the acceleration due to fluid spacetime in galaxies that is consistent with MOND and thus ensures scale invariance and is valid for most observed galaxies.
aF = 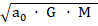 / R (4)
/ R (4)
which departs from Newtonian gravitational acceleration:
aN = (G · M) / R2 (5)
Let us now compare (4) and (5) with MOND’s predictions and check whether scale invariance and the observed relation of acceleration vs radial distance hold. In Fig 6 we plot acceleration vs radial distance from the galactic center according to (4) and (5) for three test masses: the currently accepted value for the Milky Way, 2·1042 Kg, as well as half and double this value. MOND’s key a0 parameter is a constant that arises as the intersection of the curvatures generated by Newtonian gravity and the Fluid Spacetime mechanism. For each test mass M, the apparent effective curvature (broad line) would be the larger of both curvatures at each point, which explains MOND’s claim that accelerations follow different functional relations for accelerations above and below the critical value a0.
According to FS, both mechanisms for the generation of curvature operate simultaneously, and it is the one with the higher curvature that is detected.

Figure 6: Accelerations in Newtonian gravity (aN, blue) and those predicted by the FS mechanism (aF, red) as a function of radial distance in galaxies. We represent the data for three galaxies: The Milky Way, a galaxy with half its mass, and one with its mass doubled. A crossover point appears at a fixed acceleration where gravitational and FS accelerations equal each other. For each radial distance R, the observed effective acceleration would be the higher of both (broad line)
The distribution of acceleration as a function of radius (Fig 6) certainly resembles MOND’s observed acceleration-radial distance relation (Fig 7).

Figure 7: The accelerations predicted by MOND closely mimic the ones resulting from the FS mechanism. (Reproduced from Milgrom 2014, with permission)
We notice that we did not modify the formula for Newtonian gravitational acceleration, but rather an additional source of spacetime curvature was postulated. For accelerations higher that a0, Newtonian dynamics and General Relativity apply and correctly describe all gravitational phenomena at non-relativistic speeds. At lower accelerations, it is equation (4) that applies, which matches MOND’s infra-a0 value. The two mechanisms, because of their different scaling with distance, soon become very different in value and one of them clearly dominates.
Consequences of The Model. Checking Out Against Observations
We outlined an intuitive, semi-quantitative model of fluid spacetime-generated acceleration and curvature that reproduces scale invariance, flat rotation curves, and the Tully-Fisher relation, just as Milgrom’s MOND does. The underlying physical model cannot be derived from currently established physical theories. Indeed, no observation analyzed in the frameworks of General Relativity or Quantum Mechanics can possibly support the model. We must resort to checking its plausibility and consistency with multiple observations, and especially with those that cannot be explained with current theories. This we shall now attempt by considering some of the main standing problems in modern astrophysics on which a large body of evidence is available and comparing FS with MOND’s predictions.
Flat Rotation Curves
Both MOND and the Fluid Spacetime mechanism (FS) predict scale invariance and flat rotation curves. Unlike dark matter, neither MOND nor FS have free variables that need fine-tuning. As Milgrom discovered back in 1983 and 2009, MOND’s scale-invariant model of gravitation leads to flat rotation curves:
V2/R = K ·  /R
/R
V2 = K ·  = constant
= constant
unlike Newtonian dynamics, where velocity decays as the square root of R:
V2/R = G · M / R2
V = 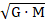 /
/ 
FS matches MOND’s predictions, which was to be expected, since the expression for the new acceleration aF exactly matches MOND’s infra-a0 modified gravitational function.
The Bullet Cluster
In the Bullet Cluster (and other similar pairs of colliding galaxy clusters), an excess of spacetime curvature is observed from gravitational lensing around the stars that constitute two galactic clusters that collided millions of years ago. The puzzling fact is that most of the mass (about 90%, as observed in X-Ray radio-telescopy), is known to consist of hydrogen, gas, and dust. This mass is located far away from the luminous stars, lagging behind the clusters themselves while they pass through each other. The location of the gas and dust is nothing to wonder about. It has long been known that they are subject to dragging forces that do not affect stars. Its location in the area in-between the two colliding clusters is well understood. But why is then the spacetime curvature located nicely and roundly just about the two groups of galaxies, away from where most of the mass is? (Fig 8). MOND cannot account for these observations.

Figure 8: The Bullet Cluster. In pink, X-Ray imaging of gas and interstellar dust that has just collided and lags behind the two groups of galaxies. In blue, location of maximal curvature of spacetime through gravitational lensing
According to the fluid spacetime mechanism, the curvature and intensity of the measured gravitational fields at large distances (or rather, at low accelerations) are dominated by the FS-induced curvature, which far outweighs the gravitational field. Since new spacetime is only generated in nuclear reactions from luminous stars, the main location of curvature should be around and near the galaxies that contain them, i.e., the blue area, with a roughly spherical distribution, as observed.
Mass Discrepancy in Galaxy Clusters
In the case of galaxy clusters, one is tempted to assume that in a group of gravitationally bound galaxies, each galaxy should behave as a point-like source of gravitational field, in a way equivalent to stars in galaxies, with each galaxy playing the role of a star. An intriguing fact with MOND is that, as much as the theory successfully describes the curvature distribution in galaxies, it fails in galaxy clusters by a factor of two to three in mass [6, 7]. The discrepancy has been attributed to experimental error or to additional undetected mass, including possibly the existence of ‘some’ dark matter.
More observations are indeed needed to confirm these findings, but according to the Fluid Spacetime mechanism, the relatively low number of galaxies contained in clusters (from 102 to 103, as compared to 1011 or more stars in a typical galaxy) violates the condition of smoothness in the distribution of spacetime curvature. Because spacetime is constantly generated at each of a low number of galaxies, the intensity of the resulting curvature does have bumps, local increases around individual galaxies inside the cluster that override the global spacetime generation of spacetime by the cluster itself. The estimation of the resulting curvature from the parameters of the cluster alone would therefore underestimate the effective curvature.
The resulting effective curvature varies locally and is expected to be anywhere between aCL, the MOND- and FS-derived value for the whole cluster, and aGAL, the likewise calculated curvature for the nearest galaxy. Hence, a higher curvature than predicted by MOND for the whole cluster should be measured in most places around an inside the cluster (Fig 9).
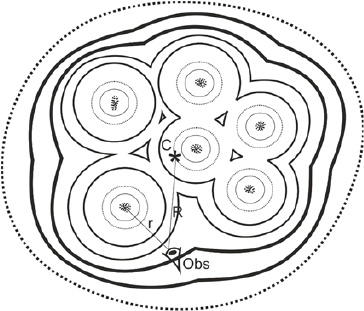
Figure 9: The effective curvature (thick lines) measured at a random point inside a cluster of galaxies (Obs) should be an intermediate value between the overall curvature calculated from MOND for the whole cluster (dotted line) and the curvature generated from the closest galaxy(s) (thin lines). C is the center of of mass of the cluster; R and r the distances from the observer to the center of mass of the cluster and the closest galaxy, respectively
Lacking a precise model of the nature and behavior of the spacetime fluid, there is currently no way to calculate what the intermediate value might be. However, based on the fact that the effective acceleration around galaxies is the geometric mean of a0 and the Newtonian acceleration, we conjecture that the analogy might be extended to galactic clusters, where two different accelerations are competing. As a first guess, we therefore try the geometric mean of aCL and aGAL.
Let RGAL be the radial distance from a test point within the cluster to the nearest galaxy, RCL the distance to the center of mass of the cluster, and Z the ratio of both radii, (Z = RCL/RGAL). The resulting acceleration aF might be conjectured as:

Which for a cluster with mass MCL composed of n galaxies with an average mass MGAL (MGAL = MCL / n) can be simplified as:
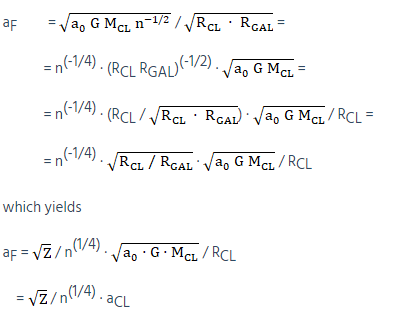
That is, the (average) corrected value for the acceleration would be MOND’s calculated value for the cluster multiplied by the factor  /n(1/4). From equation (4), this factor squared (Z/
/n(1/4). From equation (4), this factor squared (Z/ ) would then provide the correction for the discrepancy in mass.
) would then provide the correction for the discrepancy in mass.
As a test example, for a small cluster consisting of 100 galaxies and measuring accelerations from a point where the quotient of both radii equals 30, the correcting factor in mass would amount to 30/10 ~ 3, not far from what has been reported. Similarly, for a 1000-galaxies cluster and a distance from an average-mass closest galaxy equal to 1/100th the distance from the cluster center, the correction factor would be about the same, 100/32 ~ 3.
Although this is only a rough estimate based on speculation, the point is made that the FS mechanism might provide a rationale for the observed deviations from MOND in galactic clusters without the need for additional matter. Unlike MOND, where a unique gravitational function is used that depends on radial distance and the enclosed cluster mass, the FS prescription is to estimate effective curvatures from an appropriate averaging function of the curvatures generated by the closest galaxy(s) and the enclosed mass of the cluster itself.
Ultra-Diffuse Galaxies
Although the Tully-Fisher relation and MOND’s predictions have been confirmed for a wide range of galaxies, including those with low surface brightness [8], there appear to be some galaxies with extremely low luminosity that do not to meet MOND’s predictions and would apparently suffer from a lack in dark matter [9-11]. It has been argued that the observations were not all reliable and, in some cases, a miscalculation of the distance to the galaxy could indeed explain the mismatch and the low gravitational fields that are measured.
While awaiting further observations, we can venture a prediction derived from FS. As mentioned above, the rate of generation of new spacetime fluid makes no difference for the decay rate of curvature as a function of R, which should scale as 1/R for a wide range of masses and spacetime generation rates. But there is a minimum that we presently cannot estimate, that would break the rule. For very low rates of luminosity and nuclear fusion activity, the diffusion of newly generated spacetime away in the periphery of the galaxy overcomes the low generation rates at the center and spacetime fluid would lose its spherical structure and its 1/R curvature decay. We should therefore expect that galaxies with extremely low luminosities would not provide enough fluid spacetime per unit time to sustain its curved structure. In these cases, only the Newtonian gravitational field and no dark matter would be detected. An additional caveat will be mentioned later when discussing black holes.
External Field Effect
One of the most striking predictions of MOND is the existence, for small satellite galaxies, of an external influence from the gravitational field of nearby host galaxies that would lower, not increase the effective gravitational field in the satellite. As much as this would violate the so-called strong equivalence principle, the fact has already been reported from carefully performed observations [12].
The Fluid Spacetime mechanism agrees with these findings. Unlike gravity, the FS is a local effect caused by the structure of a spacetime fluid far away from the source and not directly connected to it. Curvature is not always additive, as in gravity. For two nearby galaxies, the opposing curvatures might counterbalance each other and the effective curvature would decrease and might even become null in the in-between space where the flows of spacetime with opposing curvatures meet each other (Fig 10). A satellite galaxy need not fall under gravitational capture from its host, since the intervening spacetime is flat. In contrast, in Newtonian gravity the ranges at which interactions occur are shorter, but once a galaxy interacts gravitationally with another, their mutual attraction is always additive, increasing at shorter distances as 1/R2.
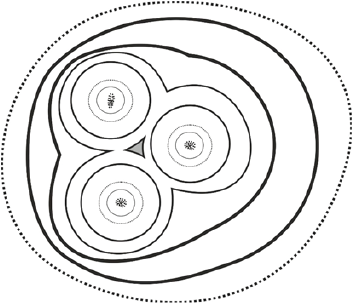
Figure 10: In FS the spacetime curvatures are a local phenomenon determined from the interaction of fluid spacetime generated from multiple neighboring sources. The effective curvature at a point between two of more galaxies might be relatively flat
A more general case can be made when several galaxies are placed roughly equidistant in space from a central point. The spacetime in the central area would acquire an approximately flat geometry (Fig 10), which would be interpreted as lacking in dark matter. The distance from the center at which galaxies would contribute maximally to this effect scales with the square root of its luminous mass' according to equation (4).
Universe Structure Formation and the CMB Data
The detection and analysis of the cosmic microwave background (CMB) radiation represents a major breakthrough in modern astrophysics and cosmology. However, when applied to the problem of dark matter, it has been less helpful, other than having been found consistent with the particle dark matter hypothesis and the concordance ∧CDM model. Verifying the agreement of FS with the CMB and with the constraints posed by structure formation at cosmic scales is currently impossible, for we lack the necessary understanding of how the fluid spacetime behaves, what are the equations that describe its distribution and flow. So, the questions for now remains moot.
And yet we should point out that
- Being dark matter a substance that only interacts gravitationally, and since Newtonian-GR gravity falls short to explaininig the observed CMB acoustic oscillations and the fast structure formation, hypotheses like MOND or FS that posit stronger curvatures and gravitational fields at large distances seem good candidates to meet the observations.
- Recent observations with gravitational lensing mapping techniques [13] convincingly claim that the distribution of curvature in galaxy clusters does not agree with current simulations of particle dark matter. The authors conclude that ‘the observed cluster substructures are more efficient lenses than predicted by ∧CDM simulations by more than an order of magnitude’, and they suggest that ‘either there might be an undiagnosed systematic issue with simulations or we are making incorrect assumptions about the properties of dark matter’. But an issue with the simulations of dark matter is a big issue, since these are particles that we cannot see nor test in the laboratory and all we know of them is based on these simulations, or in the assumptions that support them. Until these issues are solved, we should stay cautious about the alleged consistency of dark matter with the CMB.
- The stronger gravitational fields observed in cluster substructures might be consistent with the previously discussed mechanism for higher effective curvatures in clusters, as compared to MOND’s predictions.
Black Holes
The discovery, theoretical development, and recent observation of black holes (BHs) constitute one of the milestones of modern astrophysics. They have been rightly called a cosmological laboratory for General Relativity and the whole topic is an extremely active field of research.
But several questions remain unsolved. Among them we highlight:
- The plausibility and physical significance of the singularities postulated at the center of BHs.
- The origin of high angular momenta around spinning BHs that generate intense magnetic fields and strong jets of galactic scales.
- The uncanny correlation of the mass of BHs with the mass -and even better, with luminosity- of the host galaxy (Magorrian relation).
- The existence of exactly one super-massive BH at the center of most if not all galaxies, suggesting an essential role in the formation and stability of galaxies.
- The existence of super-massive BHs already at early stages of the universe [14, 15], which questions their slow development by accretion of surrounding gas and stars and leaves many questions in the open.
- Recent unpublished data [16] on the stars orbiting the Sgr A* BH in the Milky Way show a weird precessional rotation with a speed and direction unpredicted by GR.
For a model that proposes a new source of spacetime curvature and apparent gravitational fields in galaxies that disguise as additional matter, it looks a reasonable hypothesis that perhaps, the masses at the center of black holes might also be in disagreement with their estimated value from either dynamical analysis or gravitational lensing. Or, put in another way, the mass discrepancies that are at the root of the dark matter problem in galaxies and clusters might be reproduced through an analogous mechanism in and around black holes.
The Fluid Spacetime mechanism postulates a steady generation of new spacetime fluid from every luminous star that slowly flows away from its source both outwards and inwards, towards the center of the galaxy. This leads one to question whether there might be a structure playing the role of a sink for the spacetime fluid, or rather for the part of it that does not diffuse away from the galaxy. Such sink would be expected to (1) be located somewhere near the center of the galaxy, and (2) show a spinning accelerated flow in its immediate surroundings, consistent with conventional knowledge and fluid dynamics regarding the flow from large reservoirs into narrow escape pipelines. These properties intuitively fit the ones observed in black holes.
Indeed, relativistic speeds and accelerations have been observed for gas and stars orbiting around black holes, requiring either the presence of huge amounts a mass concentrated in a small central volume, as the theory predicts, or the presence of strong additional curvatures from an as yet undetermined origin.
In keeping with the proposed FS mechanism for galaxies, we hypothesize that a certain amount of fluid spacetime originating from all the stars in the galaxy flows into a centrally located sink co-located with its supermassive black hole, generating an additional spacetime curvature which would manifest as strong gravitational fields.
The process would be analogous to the one postulated at the periphery of galaxies. However, spacetime curvature around the central black hole does arise from a different mechanism and might not decay as 1/R like in galaxies. Observations around Milky Way’s black hole Sgr A* by Ghez and Genzel [17, 18] indicate that curvature around black holes decays as 1/R2, generating Keplerian or nearly-Keplerian orbits.
We will now look into the distribution of curvature around the central region of galaxies that would be expected from the FS model. We shall make the following assumptions:
- The central region of the galaxy is viewed as a spherical 3D space, and spherical symmetry will be assumed throughout. We speak of the R-sphere when referring to phenomena at radial distance R.
- A certain fixed fraction of the fluid spacetime generated at all the stars in the galaxy does not distribute away from it but rather flows slowly inwards and converges to a sink point O in its center. From previous considerations, total centripetal spacetime flow (Q) is largely constant and, for any given radius R, it is equal to the time derivative of the volume of the spacetime R-sphere centered at O.
- A curvature at the surface of the R-sphere is generated from the convergence of new spacetime fluid coming from the stars of the galaxy onto that surface. Curvature can be estimated by how much the actual radius exceeds the radius calculated by Euclidean geometry after the introduction of a certain modification in the R-sphere [19]. Usually it is the presence matter, but we postulate that the flow of spacetime can also induce such a modificaton. Since the Euclidean curvature in the R-sphere depends on the radial distance, curvature will be defined as the derivative of the effective radius with respect to that distance (dR/dx).
- Local curvature at radius R scales with the rate of new spacetime that converges to a point in the surface of the R-sphere. Since from (ii) a fixed fraction of all the generated spacetime in the galaxy contributes to populate that R-surface with new spacetime, curvature scales with the mass of the galaxy and with the total spacetime flow at its center (Q) (Fig 11).
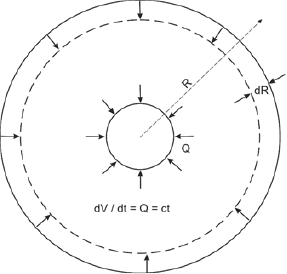
Figure 11: Spacetime around a central black hole is modeled as a fluid flowing in towards the center, with spherical symmetry and constant centripetal flow.
We can now ask ourselves how would curvature scale with radial distance R. Let us take the volume of the R-sphere V = 4/3·π·R3 and differentiate with respect to the radius R,
dV/dR = 4πR2
A small (negative) increment of the volume at fixed radius R is then
dV = 4πR2 · dR
and dividing both sides into an arbitrarily small-time interval dt
dV/dt = 4πR2 · dR/dt or, equivalently,
dR/dt = dV/dt / 4πR2 (6)
But dV/dt is the (constant) rate of flow of spacetime Q, and dR/dt is related to the curvature (defined as dR/dx), though not exactly equal. Since the strong curvatures close to the BH are expected to generate significant deformations of spacetime, this would cause the slope of dt/dx to diverge from unity. In the Schwartzschild metric the slope of light trajectories becomes higher than unity and the same would be expected for the trajectories of slow-moving objects such as stars,
dt/dx >= 1 (7)
The deviation should be small, as befits the relativistic spacetime deformations from gravity, and yet not negligible, for we are talking here of the strongest accelerations observed in nature. From eqs (6) and (7), we have
Curvature: = dR/dx = dR/dt·dt/dx >= dR/dt = (dV/dt)/4πR2 = Q/4πR2 (8)
Which means that Q/4pR2 would be an approximation and a lower bound for curvature around the black hole. Since Q is constant and we can fix a certain radius R, we define n as the exponent to which R must be raised to make the following equality hold:
(Q / 4πR2) ·(dt/dx) = Q / 4πRn
where n is such that
R2/Rn = dt/dx >= 1,
and we obtain the following expression for curvature at radius R.
dR/dx = Q/4pRn (n < 2, n ≅ 2)
And since (from iv) Q scales with the galactic mass MGAL, the simplest polynomial expression for curvature around black holes based on measurable quantities that fulfills the assumptions is:
AccelFS:= dR/dx = H MGAL / Rn (n < 2, n ≅ 2) (9) (Figs 12, 13)


Figures 12 and 13: Postulated distribution of accelerations around a black hole as a function of radial distance in linear and log-log scales. Represented are data for Milky Way’s Sgr A* for Newtonian gravity (aN, black) and for FS at different values of n (aF, blue, red, green). For n>2, a crossover point appears for Newtonian and FS accelerations (vertical line). For n<2, FS remains larger than Newtonian acceleration
where MGAL is the galaxy mass, R is radial distance, and we collected all the linear constants under H, including 4π, the fraction of the galactic mass that contributes to new spacetime flow into the black hole, and the constant relating galactic mass to fluid flow Q. Curvature would be thus determined by the mass of the galaxy and would scale as 1/Rn, for n slightly smaller than two. Interestingly, this would result in non-closed elliptical orbits that would deviate from both Newtonian mechanics and GR, for it is well known that the only decay law that results in closed, elliptical orbits is the exact 1/R2. There are arguments that indicate that, for n slightly lower than 2, a precession of stars’ orbits arises in the opposite sense than the orbits of the stars, a finding that has been recently communicated for Sgr A* by Prof Ghez [16]. In fact, American astronomer Asaph Hall already attempted to solve the problem of the precession of mercury in the early 20th century by assuming that Newton’s inverse square law did not hold exactly [20], the attraction between two bodies varying as 1/r2(1+d), where d is 1/13,000,000. This new law would correctly explain the discrepancy so far as Mercury was concerned but introduced a discrepancy in the nearest position of the moon to the earth, known as the moon’s perigee and was therefore swiftly ruled out and forgotten.
Since it is postulated that both the FS and the Newtonian representations hold true for any radial distance R, we can equate both,
H·MGAL / Rn = G·MBH / R2
And since since Rn/R2 is close to one and remains relatively constant over a wide range of radial distances, we obtain an approximately linear relation between galactic mass and the mass of the black hole:
MGAL = (G / H) ·(Rn/R2) · MBH ≅(G/H) · MBH (10)
MGAL ~ MBH
which is actually the Magorrian relation for mass.
In summary, the extension of the FS mechanism to black holes hints at the possibility of strong accelerations arising in black holes through the convergent flow of spacetime that are consistent with ‘nearly Keplerian’ orbits, providing an alternative explanation for the extreme masses that appear to concentrate in them. The very center of that region would still remain an elusive, weird place with extreme curvatures, large energy outputs and an unknown mass content, but not necessarily a mathematical singularity.
A Little Digression on Numerology
Although we deeply distrust the so-called ‘numerological’ arguments, the fact cannot be overlooked that, assigning the currently accepted values for the Milky Way of MBH (4.1·106 solar masses, or 8·1036 Kg), and MGAL (1012 solar masses, 2·1042 Kg) and assuming Rn/R2 close to unity, from equation (10) the estimated value of the constant H for the Milky Way would be:
H ≅ G · MBH / MGAL ≅ 2.5 · 10-16
which -very likely by chance- approximates within one order of magnitude to
H ≅ 2.5 · 10-16 ≅ 7·10-16 = 10-5 · 7· 10-11 ≅  · G
· G
Further Comments on Black Holes
It is unclear whether the spiraling movement observed in black holes as part of the accretions disk -their spin- would involve just the matter -stars, dust and gas- that orbits around them, or also spacetime fluid itself. Considering that a fast-spinning fluid would lose its ability to preserve its curvature across large distances and time scales, it seems more likely that the spin and angular momentum in black holes be caused by the spiraling gas and matter that are captured in the strong gravitational well at its center, and the fluid spacetime itself would be relatively static with regards to rotation.
From this point onward things get extremely complicated, with gas and matter at high velocities and temperatures, meeting spacetime at huge densities and curvatures at the center. This might result in the large energy outputs in the form of radiation and jets that are observed in some supermassive BHs. These have been for decades the hallmark of quasars, and indeed remain one the most spectacular and mysterious aspects of these intriguing structures. We can only speculate with the possibility that the reverse form of the Einstein equation (1) might perhaps take place in some black holes, since both main ingredients, spacetime and energy would be present in large amounts.
Some comment seems appropriate with regards to the characteristic lack of visible light emerging from the center of black holes. According to the GR-Schwartzschild model, this essential property that defines blackholes is caused by extreme gravitational fields, the escape velocity of which overcomes even the speed of light. But it is also be consistent with FS, where extreme curvatures are posited at the center. Indeed, the intensity of the observed light coming from the center of black holes according to the FS mechanism is expected to be very low. First, because only small amounts of light might be generated, but also because the extreme bending of spacetime fluid would induce diverging and possibly changing light paths that would make its intensity extremely low for a far-away observer. In fact, a radius can also be defined where curvature overcomes the light’s escape velocity, and this would take place at even larger distances, depending on how much R2/Rn deviates from unity.
On the Expansion of the Universe and Dark Energy
But where –it might be asked- does all the spacetime fluid end up after being collected at a central sink in black holes? What might be the fate of such huge amounts of fluid spacetime? Since the local outward expansion of spacetime both away from and towards the center of galaxies would need to be a slow process, as demanded by the preservation of curvature, this mechanism cannot account for an effective spacetime expansion in a homogeneous universe. At most, it might give rise to relatively small bubbles of spacetime around galaxies and galaxy groups. Without delving into the details of a theory that we are in no position to accurately describe, we hint at the possibility that gravitational waves that are emitted from black holes, of which only the most intense ones from mergers have actually been detected, might be the ultimate fate of spacetime. If that was the case, we can tentatively imagine all the spacetime fluid generated in galaxies being collected at intermediate relay stations in their central region co-located with a black hole and spreading at the speed of light throughout the universe, i.e, it might constitute a basis for the mysterious phenomenon of dark energy. The rate of the universe expansion would then depend on the nuclear reactions taking place at all the stars in the universe in exact correspondence with the amount of mass consumed by them and subject to a considerable time lag, the time that it takes for the fluid to slowly travel from its source stars to the galactic center. From there, spacetime would then be expelled at the speed of light into the cosmos, where it might manifest as a homogeneous spacetime expansion.
As an unexpected consequence, the total mass-energy budget of the universe might be again conserved, preserving the law of conservation of energy. The rate of expansion of the universe would have a limit, namely that of the available mass in stars, after which the expansion would need to slow down and eventually reverse. Finally, a cyclic cosmology would result, but one grounded on a fixed, stable universal mass-spacetime reservoir, where the expansion and contraction phases could possibly be predicted or at least understood.
We are aware that these ideas are only conjectures with no direct supporting evidence. But new theoretical developments are rarely if ever supported by direct evidence. Their confirmation comes from agreement of predictions with past and -specially- with future observations targeted at their testing. It is our claim that, if one gives some credit to the FS mechanism, these ideas are difficult to sideline. Its grounding on MOND -a solid theoretical construct that has proved its consistency through decades- and the additional explanatory power on a handful of hard long-standing problems in astrophysics support the idea that indirect, circumstantial evidence might be worth considering. New insights are proposed into the nature of dark matter, dark energy and black holes. Black holes would no longer need to harbor mathematical singularities, and their role as essential structural elements in galaxies and the whole cosmos might be better understood.
In the end, theories are good only insofar as they lead us to predictions that can be tested by observations. A tentative, likely incomplete list of testable observations for the FS mechanism would include:
- Galaxy rotation curves consistent with MOND should be observed for a wide range of rotationally-supported galaxies. MOND and FS predictions fully agree with regards to galaxy dynamics.
- Curvatures in galaxy clusters might be assessed from the observed masses when curvatures are averaged over local galaxy curvatures and curvature due to the mass of the whole cluster, on the lines described above. This seems to be a feasible test with the available evidence from ongoing gravitational lensing mapping studies.
- Co-location of curvature with luminous matter, not with total matter in colliding galaxy clusters.
- The existence of galaxies with very low luminosity and no discrepancy in mass, i.e., without dark matter, is predicted by FS. However, one must also take into account the influence of the central black hole. In its absence, or when a very small black hole is present, one might still expect that low rates of spacetime generation would suffice in producing an effective additional curvature and therefore simulate the presence of significant amounts of dark matter. The end result might imply an equilibrium between the rate of spacetime generation from stars and the efficiency of the central collecting mechanism at the black hole.
- The flattening of intermediate space between close-by galaxies (MOND’s External Field Effect) might be generalized to groups of galaxies. The effect would be maximal in groups of equidistant, symmetrically placed galaxies whose distances from the center of the cluster scale as the square root of their masses.
- The relation of MOND’s a0 parameter with the cosmological constant ∧ and the Hubble parameter H0 might be better understood, as they would all reflect a basic underlying process of spacetime generation from mass via nuclear reactions. Though clearly a difficult and far-fetched aim for now, the evolution of H0 through cosmological times might eventually be ascertained from models that include FS, the total amount of luminous mass and the average time lag needed for the fluid spacetime to reach the galactic center from their source stars.
- The anomalous distribution of gravitational fields observed by Ghez and cols. around Sgr A*, with orbital precessions that strongly depart from GR (16), might also be used as a test case. Newtonian dynamics predicts perfectly eliptical orbits for all stable orbiting stars, and it is only GR that introduces a deviation in the form of a precession that is always in the same sense as the orbit of the star. According to Prof Ghez, “It (SO-2’s orbit) is doing the exact opposite of what is expected”. She hinted at the possibility that some dark matter might be needed to fix the discrepancy. We can only add that if inverse precessions around Sgr A* are confirmed, the FS mechanism with a 1/Rn decay and n smaller than 2 might be a candidate explanation without the contribution of dark matter.
There are indeed several limitations in this study. To name a few, It lacks a mathematical description of fluid spacetime, its properties and behavior. This is logical, for these are new concepts, and certainly difficult to describe mathematically. Take the behavior of fluid spacetime for instance. Assuming that spacetime can behave like a fluid looks like a natural extension to GR. However, the equations that describe the flow of a massless, viscosity-free fluid that generates and conserves curvature while moving comes like the exact opposite of the main assumptions in the Navier-Stokes equations, the cornerstone of fluid dynamics. For anyone who might aim at further developing these ideas, the task ahead looks immense. For that reason, the expedite and cost-effective way to proceed might be to first check out its consistency with the available astrophysical observations.
Only rotationally-supported spiral galaxies with a random, uniform distribution of stars have been considered. This was done of course to benefit from spherical symmetry and simple dynamics. Although ellipticals and irregulars might eventually fit the same pattern, this is not quite so clear.
Our simplified model of BHs does not take into account the possible spinning of the spacetime fluid around BHs. If it did happen, it might increase the spacetime curvatures from the ones predicted here. Also, most available data on the Magorrian relation apply to the mass of the central bulge, to luminosity, or to the velocity dispersion of stars. As mentioned, these would be expected to scale with the mass of the whole galaxy, provided a fixed fraction of it contributes to the flow of spacetime fluid into the BH.
How are to be interpreted the precise predictions of BHs’ masses provided by LIGO observations of gravitational waves (GWs)? The masses of colliding BHs in LIGO lack an independent source for their measurement and yet the concordance with theoretical simulations is remarkable. No discrepancies are found here. In FS on the other hand, the immature and semi-quantitative nature of the model does not allow a precise description of the resulting GWs. However, to settle conclusively the issue of BHs masses we would need to predict in advance which BHs are going to collide and study their masses by other independent means, and this does not seem currently possible.
Besides a much-needed full mathematical model of fluid spacetime and its comparison with new observations, the assessment of the equivalence matter-spacetime -λ and β in equation (1) would be high in the list of priorities and might stimulate further developments.
Also, there have been some arguments in the context of MOND on the precise significance of a0 and its relation to the constants G and ∧. Although the issue exceeds the present discussion, we hope that the fluid spacetime mechanism, if confirmed, may contribute to illuminate these questions -why two constants, a0 and G, are needed to explain all gravitational phenomena, and why a0 scales with the square root of the cosmological constant ∧.
Lastly, on a more theoretical note, the identity of inertial and gravitational mass (the equivalence principle) might find a rationale in the proposed equivalence mass-spacetime. Indeed, in the FS framework both inertia -the strength with which mass is bound to the neighboring space- and gravity -how much deformation of surrounding space is caused by a mass- can be intuitively linked to the amount of spacetime that is trapped within a certain mass, ready to be released when a nuclear reaction takes place.
We are indebted to Mordehai (Motti) Milgrom for his pioneering role in developing MOND and for the many insights we gained from his published works.
Our brother (AF) and friend (GS) Josep M. Francino offered invaluable help with his expertise in the mathematical software Mathematica® and contributed many useful suggestions.
To the professional physicists who took the trouble to look at a draft of the paper, we thank them for their patience and encouragement.
- Milgrom, M (1983) A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. ApJ 270: 365-370.
- Milgrom, M (2009) The Mond Limit from Spacetime Scale Invariance. ApJ 698: 1630-1638.
- Milgrom, M (2014) The MOND paradigm of modified dynamics. Scholarpedia 9: 31410.
- Sanders, R.H., McGaugh, S.S (2002) Modified Newtonian Dynamics as an Alternative to Dark Matter. Annu. Rev. Astron. Astrophys 40: 263.
- Sachs, M (2007) Concepts of Modern Physics - The Haifa Lectures. Imperal College Presss, London, p. 84.
- Sanders, R. H (1999) The Virial Discrepancy in Clusters of Galaxies in the Context of Modified Newtonian Dynamics. The Astrophysical Journal 512: L23-L26.
- Milgrom, M (2019) MOND in galaxy groups: A superior sample. arXiv:1811.12233v2.
- De Blok., WJG, McGaugh S (1997) The dark and visible matter content of low surface brightness disc galaxies, MNRAS 290: 533-552.
- Van Dokkum Pieter., Cohen Yotan., Danieli Shany (2018) An Enigmatic Population of Globular Clusters in a Galaxy Lacking Dark Matter. The Astrophys J Letters, 856: L30.
- Van Dokkum Pieter., Danieli Shany., Abraham Roberto (2019) The Astrophys J letters, 874: L5.
- Asencio E., Banik I., Mieske S., Venhola A., Kroupa P., et al. (2022) The distribution and morphologies of Fornax Cluster dwarf galaxies suggest they lack dark matter. MNRAS 000, 1-35.
- Chae Kyu-Hyun., Lelli Federico., Desmond Harry., McGaugh Stacy., Li Pengfei., et al. (2020) Testing the Strong Equivalence Principle: Detection of the External Field Effect in Rotationally Supported Galaxies. The Astrophysical Journal 904: 51.
- Meneghetti Massimo., Davoli Guido., Bergamini Pietro., Rosati Piero., Natarajan Priyamvada (2020) An excess of small-scale gravitational lenses observed in galaxy clusters. Science 369:1347-1351.
- Wu Xue-Bing., Wang Feige., Fan Xiaohui (2015) An ultraluminous quasar with a twelve-billion-solar-mass black hole at redshift 6. 30. Nature (letter) 518: 513-515, 2015.
- Alexander, Tal., Natarajan, Priyamvada (2014) Rapid growth of seed black holes in the early universe by supra-exponential accretion. arXiv 1408.1718v2.
- Ghez, Andrea (2022) lecture, YouTube video “From the Possibility to the Certainty of a Supermassive Black Hole - Andrea Ghez (UCLA)” (51: 30).
- Ghez A.M., Salim S., Weinberg N.N., Lu, J.R., Do, T., et al. (2008) Measuring distance and properties of the Milky Way’s central supermassive black hole with stellar orbits. Astrophysical Journal 689: 1044-1062.
- Eckart, A., Genzel, R (1996) Observations of stellar proper motions near the galactic center. Nature 383: 415.
- Feynman Richard (1995) Lectures on Gravitation. Addison-Wesley Reading, Mass 154.
- Davidson, Martin (1962) Elements of Mathematical Astronomy. Hutchinson, London 3rd ed: 252.


 (1)
(1)