In four dimensions, the Minkowski metric 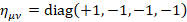 leads to the 16 dimensional Clifford algebra C(1,3), Dirac equation is using four of these 16 matrices that form a basis of this algebra, a new operator is defined using all of these matrices and also generalized for a curved space
leads to the 16 dimensional Clifford algebra C(1,3), Dirac equation is using four of these 16 matrices that form a basis of this algebra, a new operator is defined using all of these matrices and also generalized for a curved space
We are using Pauli matrices σ, electromagnetic four-potential Aμ and charge e with  [1].
[1].
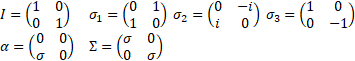 (1)
(1)
In four dimensions, Minkowski's metric 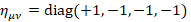 leads to the Clifford algebra C
leads to the Clifford algebra C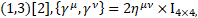 Dirac matrices
Dirac matrices 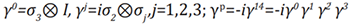
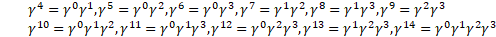 (2)
(2)
Multilevel operator Dn acts on level n, n is the number of matrices in the product of the algebra members, for example, D3 acts on 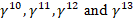 . Total multilevel operator Dmul = D0 +D1 +D2 +D3 +D4, the action of Dmul on the spinor function vanishes
. Total multilevel operator Dmul = D0 +D1 +D2 +D3 +D4, the action of Dmul on the spinor function vanishes 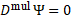
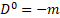 (4)
(4)
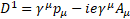 (5)
(5)
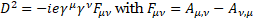 (6)
(6)
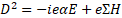 (7)
(7)
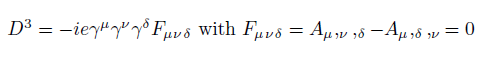 (8)
(8)
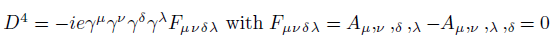 (9)
(9)
Multilevel operator Dmul(ημν ,Aμ ,e) can be generalized for a curved space with four-potential P, field charge q and covariant derivative[3] (;μ) instead of derivative (,μ) in the definition of 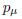
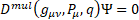 (10)
(10)
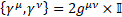 (11)
(11)
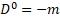 (12)
(12)
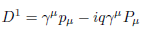 (13)
(13)
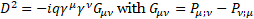 (14)
(14)
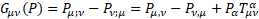 (15)
(15)
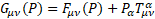 (16)
(16)
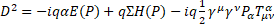 (17)
(17)
For gravity 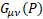 is the new gravitomagnetic tensor.
is the new gravitomagnetic tensor. 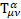 is the torsion tensor [4].
is the torsion tensor [4].
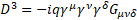 with
with 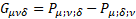 (18)
(18)
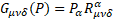 with
with 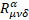 the Riemann-Christoffel tensor [5]. (19)
the Riemann-Christoffel tensor [5]. (19)
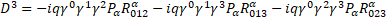
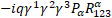 (20)
(20)
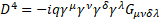 with
with 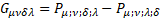 (21)
(21)
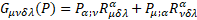 (22)
(22)
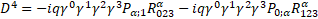 (23)
(23)
Multilevel operator 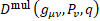 has been generalized for a curved space with a general four-potential P. For gravity
has been generalized for a curved space with a general four-potential P. For gravity 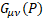 is the new gravitomagnetic tensor and torsion tensor
is the new gravitomagnetic tensor and torsion tensor 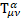 appears in its definition.
appears in its definition.
In a flat space 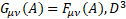 and
and 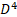 operators vanish. In a curved space the curvature tensor
operators vanish. In a curved space the curvature tensor 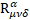 appears in levels 3 and 4.
appears in levels 3 and 4.
The appearance of torsion tensor 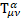 and curvature tensor
and curvature tensor 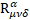 in multilevel operator
in multilevel operator 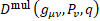 means that this operator is a fundamental operator in Quantum Field Theory.
means that this operator is a fundamental operator in Quantum Field Theory.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 637.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 650-652.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 380.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 384.
- Marian Fecko (2006 Differential Geometry and Lie Groups for Physicists. Cambridge University Press 404.
Editorial Information
Article Type
Short Communication
Publication history
Received date: January 15, 2022
Accepted date: January 21, 2023
Published date: January 31, 2023
Copyright
©2023 Delso J. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Citation
Delso J (2023) On Generalized Dirac's Equation. OSP Journal of Physics and Astronom 4: JPA-4-142.
Corresponding author
Jesus Delso Lapuerta
Bachelor's Degree in Physics by Zaragoza University, Spain. jesus.delso@gmail.com

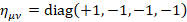 leads to the 16 dimensional Clifford algebra C(1,3), Dirac equation is using four of these 16 matrices that form a basis of this algebra, a new operator is defined using all of these matrices and also generalized for a curved space
leads to the 16 dimensional Clifford algebra C(1,3), Dirac equation is using four of these 16 matrices that form a basis of this algebra, a new operator is defined using all of these matrices and also generalized for a curved space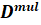
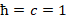 [1].
[1].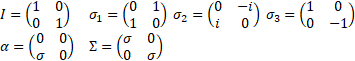 (1)
(1)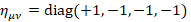 leads to the Clifford algebra C
leads to the Clifford algebra C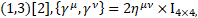 Dirac matrices
Dirac matrices 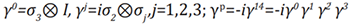
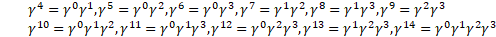 (2)
(2)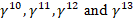 . Total multilevel operator Dmul = D0 +D1 +D2 +D3 +D4, the action of Dmul on the spinor function vanishes
. Total multilevel operator Dmul = D0 +D1 +D2 +D3 +D4, the action of Dmul on the spinor function vanishes 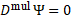
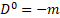 (4)
(4)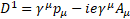 (5)
(5)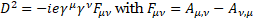 (6)
(6)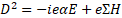 (7)
(7)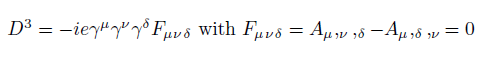 (8)
(8)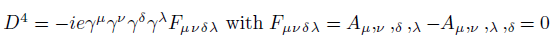 (9)
(9)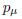
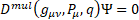 (10)
(10)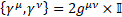 (11)
(11)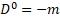 (12)
(12)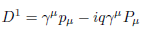 (13)
(13)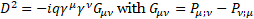 (14)
(14)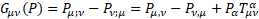 (15)
(15)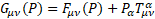 (16)
(16)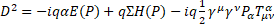 (17)
(17) is the new gravitomagnetic tensor.
is the new gravitomagnetic tensor.  is the torsion tensor [4].
is the torsion tensor [4].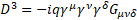 with
with 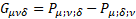 (18)
(18)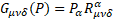 with
with 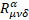 the Riemann-Christoffel tensor [5]. (19)
the Riemann-Christoffel tensor [5]. (19)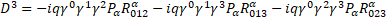
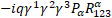 (20)
(20)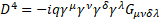 with
with 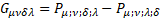 (21)
(21)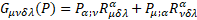 (22)
(22)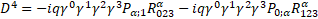 (23)
(23)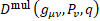 has been generalized for a curved space with a general four-potential P. For gravity
has been generalized for a curved space with a general four-potential P. For gravity 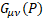 is the new gravitomagnetic tensor and torsion tensor
is the new gravitomagnetic tensor and torsion tensor 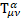 appears in its definition.
appears in its definition.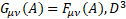 and
and 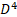 operators vanish. In a curved space the curvature tensor
operators vanish. In a curved space the curvature tensor 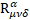 appears in levels 3 and 4.
appears in levels 3 and 4.