In four dimensions, the Minkowski metric ημν = diag (+1,—1,—1,—1) leads to the 16-dimensional Clifford algebra C(1,3), Dirac's equation [1] is using four of these 16 matrices that form a basis of this algebra, a new operator is defined using all of these matrices and also generalized for a curved space. This new multilevel operator generalizes the Dirac's equation, the value of the generalize Dirac's operator is calculated in the Schwarzschild's metric
Gravitomagnetic Tensor; Gravitational Magnetic Field; Energy Momentum 1-Form; Clifford Algebra; Dirac Equation; Dirac Operator; Gravity and Quantum Mechanics Unification; Multilevel Operator; Schwarzschild's Metric
Dirac's equation is the relativistic wave equation derived by physicist Paul Dirac in 1928. The wave functions in the Dirac theory are vectors of four complex numbers (known as bispinors), two of which resemble the Pauli wavefunction in the non-relativistic limit, in contrast to the Schrodinger equation which described wave functions of only one complex value.
Dirac's operator is just the tip of the iceberg, the tip of a generalized operator that is obtained by operating on all members of the Clifford algebra basis and not just on four of them.
The Schwarzschild's metric is named in honour of Karl Schwarzschild, who found the exact solution in 1915 and published it in January 1916, a little more than a month after the publication of Einstein's theory of general relativity. It was the first exact solution of the Einstein field equations other than the trivial at space solution. Schwarzschild died shortly after his paper was published, as a result of a disease he developed while serving in the German army during World War I. Johannes Droste in 1916 independently produced the same solution as Schwarzschild.
Schwarzschild's metric is an exact solution to the Einstein's field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant is all zero.
The new generalized Dirac's operator, the multilevel operator, is calculated in the Schwarzschild's metric, torsion tensor and new gravitomagnetic tensor appear in level 2, curvature tensor appears in levels 3 and 4.
We are using Pauli matrices σ, electromagnetic four-potential Aμ and charge e with 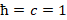 [1].
[1].
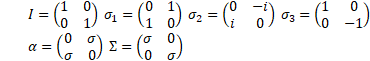 1
1
In four dimensions, Minkowski's metric ημν = diag (+1,-1,-1,-1) leads to the Clifford algebra C(1,3)[2], 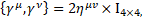 Dirac matrices
Dirac matrices 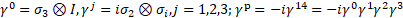
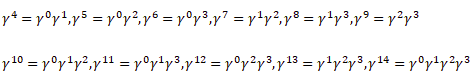 2
2
Multilevel operator Dn acts on level n, n is the number of matrices in the product of the algebra members, for example, D3 acts on γ10, γ11, γ12, and γ13. Total multilevel operator 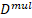 = D0 +D1 +D2 +D3 +D4, the action of
= D0 +D1 +D2 +D3 +D4, the action of 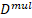 on the spinor function vanishes
on the spinor function vanishes 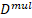 ψ=0 3
ψ=0 3
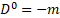 4
4
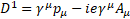 5
5
 6
6
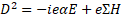 7
7
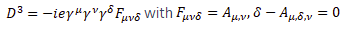 8
8
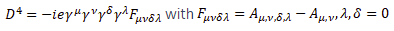 9
9
Multilevel operator 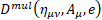 can be generalized for a curved space with four-potential P, field charge q and covariant derivative [3]
can be generalized for a curved space with four-potential P, field charge q and covariant derivative [3] 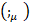 instead of derivative
instead of derivative 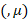 in the definition of
in the definition of 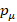
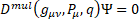 10
10
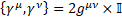 11
11
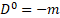 12
12
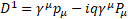 13
13
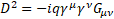 with
with 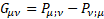 14
14
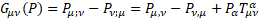 15
15
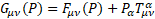 16
16
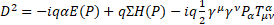 17
17
For gravity 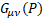 is the new gravitomagnetic tensor.
is the new gravitomagnetic tensor. 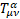 is the torsion tensor [4].
is the torsion tensor [4].
 18
18
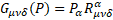 with
with 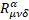 the Riemann-Christoffel tensor [5]. 19
the Riemann-Christoffel tensor [5]. 19
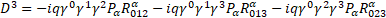
 20
20
 21
21
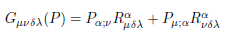 22
22
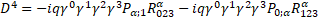 23
23
We are using 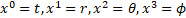 with
with 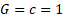 , this metric is defined by [6]
, this metric is defined by [6]
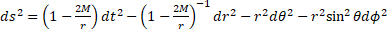 24
24
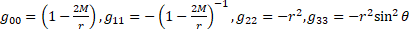 25
25
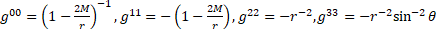 26
26
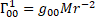 27
27
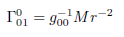 28
28
 29
29
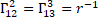 30
30
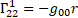 31
31
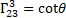 32
32
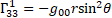 33
33
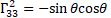 34
34
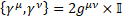 35
35
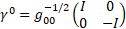 36
36
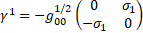 37
37
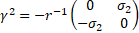 38
38
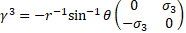 39
39
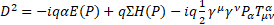 , from equations (16) and (17) 40
, from equations (16) and (17) 40
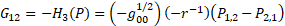 41
41
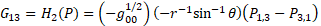 42
42
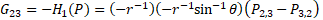 43
43
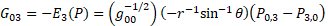 44
44
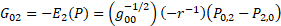 45
45
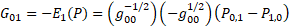 46
46
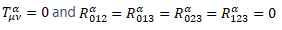 47
47
Energy-momentum form is a 1-form [7]
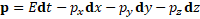 48
48
dp is a 2-form
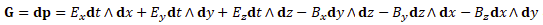 49
49
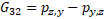 50
50
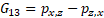 51
51
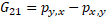 52
52
Comparing equations (41-43) and (50-52) we can infer
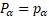 53
53
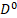 is related to the scalar 0 -form
is related to the scalar 0 -form 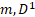 is related to the Energy-momentum 1-form,
is related to the Energy-momentum 1-form, 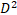 is related to the Electromagnetic 2 -form,
is related to the Electromagnetic 2 -form, 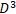 is related to
is related to
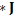 3-form [8].
3-form [8].
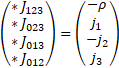 54
54
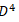 is related to L 4-form [9].
is related to L 4-form [9].
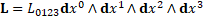 55
55
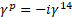 is the proyector matrix, historically
is the proyector matrix, historically 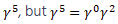
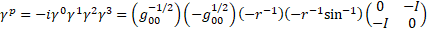 56
56
Multilevel operator 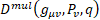 has been generalized for a curved space with a general four-potential P. For gravity
has been generalized for a curved space with a general four-potential P. For gravity 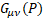 is the new gravitomagnetic tensor and torsion tensor
is the new gravitomagnetic tensor and torsion tensor 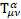 appears in its definition.
appears in its definition.
In a flat space 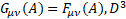 and
and 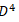 operators vanish. In a curved space the curvature tensor
operators vanish. In a curved space the curvature tensor 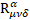 appears in levels 3 and 4.
appears in levels 3 and 4.
The appearance of torsion tensor 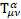 and curvature tensor
and curvature tensor 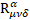 in multilevel operator
in multilevel operator 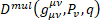 means that this operator is a fundamental operator in Quantum Field Theory.
means that this operator is a fundamental operator in Quantum Field Theory.
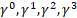 , have been calculated for Schwarzschild's metric, then
, have been calculated for Schwarzschild's metric, then 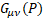 , the gravitomagnetic tensor has been obtained
, the gravitomagnetic tensor has been obtained
Each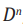 , where n is the number of γ matrices in the product of the algebra members, is related to an n-form.
, where n is the number of γ matrices in the product of the algebra members, is related to an n-form.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 637.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 650-652.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 380.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 384.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 404.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University 30-32.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 91.
- Roger Penrose (2006) El camino a la realidad. Random House Mondadori, 603.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 119.

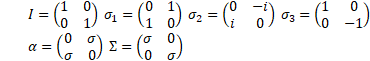 1
1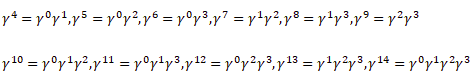 2
2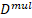 = D0 +D1 +D2 +D3 +D4, the action of
= D0 +D1 +D2 +D3 +D4, the action of  6
6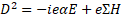 7
7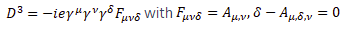 8
8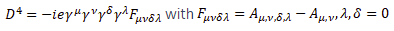 9
9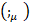 instead of derivative
instead of derivative 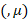 in the definition of
in the definition of 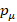
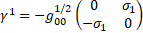 37
37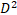 is related to the Electromagnetic 2 -form,
is related to the Electromagnetic 2 -form, 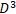 is related to
is related to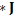 3-form [8].
3-form [8].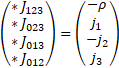 54
54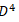 is related to L 4-form [9].
is related to L 4-form [9]. 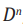 , where n is the number of γ matrices in the product of the algebra members, is related to an n-form.
, where n is the number of γ matrices in the product of the algebra members, is related to an n-form.