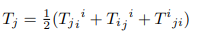Electromagnetic tensor is a 2-form derived from the exterior derivative of a 1-form, similarly Gravitomagnetic tensor can be derived from the exterior derivative of the Energy-momentum 1-form and we obtain the similar Maxwell`s equations.
In a manifold with a linear connection if the torsion tensor vanishes then the Christoffel symbols are symmetric in the lower indices, this is the motivation to call it the symmetric connection.
The requirement of being metric, the length is preserved by parallel transport, and symmetric leads to the unique result for the Christoffel symbols of the connection.
This distinguished linear connection on a Riemannian manifold is usually called the Riemann connection or the Levi-Civita connection.
We consider a connection which is metric but not symmetric, the torsion tensor does not vanish and we study the conservation laws depending on it and the action, the space is a Riemann-Cartan space.
Gravitomagnetic Tensor; Energy-Momentum 1-Form; Riemann-Cartan Space; Curvature 2-Form; Maxwell`s Equations; Metric Connection; Twisted Space; Torsion Tensor; Contorsion Tensor; Conservation Law; Curved Space; General Relativity; Riemann Curvature Tensor; Ricci Tensor
Galaxies in our universe are rotating with such speed that the gravity generated by their observable matter could not possibly hold them together, an extra force is needed to explain it.
This extra force also defines the distribution of galaxies in the universe.
Electromagnetic form is a 2-form [1].
F = −Exdt ∧ dx − Eydt ∧ dy − Ezdt ∧ dz + Bxdy ∧ dz + Bydz ∧ dx + Bzdx ∧ dy (1)
Energy-momentum form is a 1-form [1].
p = −Edt + pxdx + pydy + pzdz (2)
Gravitomagnetic form is a 2-form
G = dp = −Exdt ∧ dx − Eydt ∧ dy − Ezdt ∧ dz + Bxdy ∧ dz + Bydz ∧ dx + Bzdx ∧ dy (3)
G01 = −Ex = px,t + E,x (4)
G02 = −Ey = py,t + E,y (5)
G03 = −Ez = pz,t + E,z (6)
G23 = Bx = pz,y − py,z (7)
G31 = By = px,z − pz,x (8)
G12 = Bz = py,x − px,y (9)
dG = ddp = 0 [2], we obtain the similar Maxwell`s equations
Div B = 0 (10)
Curl E = −B,t (11)
* is the Hodge dual [2].
*G = Bxdt ∧ dx + Bydt ∧ dy + Bzdt ∧ dz + Exdy ∧ dz + Eydz ∧ dx + Ezdx ∧ dy (12)
d* G = 4π *J [2], we obtain the last 2 equations with ρ, the mass density
Div E = 4πρ (13)
Curl B = E,t + 4πJ (14)
where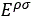 is the stress-energy tensor of the field.
is the stress-energy tensor of the field.
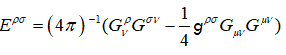 (15)
(15)
The Christoffel symbols of the first kind of the connection with a given torsion T satisfy [3].
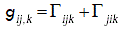 (16)
(16)
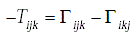 (17)
(17)
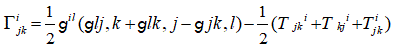 (18)
(18)
Differentiating the determinant g [4] and defining 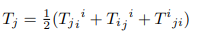
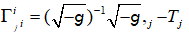 (19)
(19)
The vector Aµ has the covariant divergence [5].
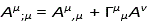 ν (20)
ν (20)
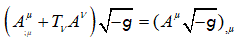 (21)
(21)
If the left-hand side of equation (21) equals zero then the right-hand side gives us the first conservation law.
For the antisymmetric tensor F µν = - F νµ [5].
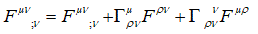 (22)
(22)
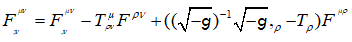 (23)
(23)
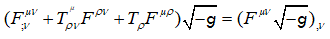 (24)
(24)
If the left-hand side of equation (24) equals zero then the right-hand side gives us the second conservation law [6].
In the symmetric case Y µν = Y νµ we can get a corresponding equation, provided we put one of the suffixes downstairs and deal with Y µν; v
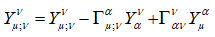 (25)
(25)
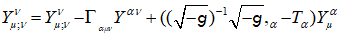 (26)
(26)
Since Y µν = Y νµ is symmetric, we can replace the 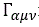 from (16) by
from (16) by
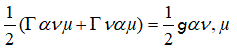 (27)
(27)
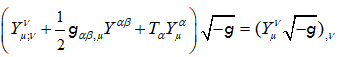 (28)
(28)
For the antisymmetric tensor Fµν = Aµ;ν – Aν;µ
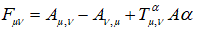 (29)
(29)
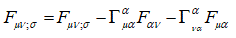 (30)
(30)
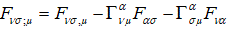 (31)
(31)
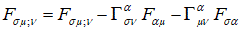 (32)
(32)
Adding equations (30), (31) and (32)
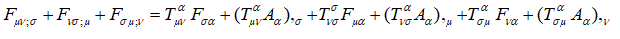 (33)
(33)
The δ1 for the antisymmetric tensor Fµν = Aµ;ν – Aν;µ [7].
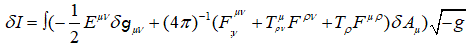 (34)
(34)
where 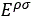 is the stress-energy tensor of the field [7].
is the stress-energy tensor of the field [7].
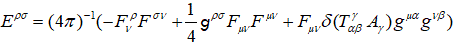 (35)
(35)
The term, 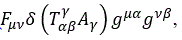 is derived from the new dependence of Fµν on torsion tensor and the dependence of Tµν on gµν .
is derived from the new dependence of Fµν on torsion tensor and the dependence of Tµν on gµν .
The other new terms depending on Tµν are derived from equation (24).
Equation (18) implies that space is a Riemann-Cartan space [8], the metric connection differs from the Levi-Civita connection by a quantity which is determined by the torsion tensor.
In a Riemann-Cartan space the exterior covariant derivative of the metric tensor vanishes implying the antisymmetric of the contorsion tensor, the contorsion tensor is precisely the quantity that measures how much a general connection differs from the Levi-Civita connection.
Tensor densities have been defined leading to conservation laws depending on the torsion, if torsion is zero these equations return to the known conservation laws in General Relativity.
Action has been defined and there are new terms depending on the torsion, if the torsion tensor vanishes this equation returns to the known action.
Gravitomagnetic tensor has been derived from the Energy-momentum and we have obtained the similar Maxwell`s equations, in a galaxy there are no dark matter particles generating the dark matter force, Gravitomagnetic tensor and new terms in the action depending on the torsion explain this extra force.
Space must also be twisted, for a complete image of the universe we need the antisymmetric part of the connection and space is a Riemann-Cartan space with a metric connection.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University Press, 91.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University Press, 113.
- Marian Fecko (2006) Differential geometry and Lie groups for Physicists. Cambridge University Press 389.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 37.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 38.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 39.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 54-55.
- Radek Suchanek (2018) Field equations of General relativity and Einstein-Cartan theory, Master Thesis, Masarykova Univerzita 38.