The solution of the Schrödinger's equation for an electron orbiting a nucleus leads us to the emission of gravitomagnetic photons when the gravitational potential is also taken into account. In four dimensions, the Minkowski metric ημν = (+1,-1,-1,-1) leads to the 16-dimensional Clifford algebra C(1,3), Dirac's equation [1] is using four of these 16 matrices that form a basis of this algebra, a new operator is defined using all of these matrices and also generalized for a curved space. This new multilevel operator generalizes the Dirac's equation, the value of the generalized Dirac's operator is calculated in the Schwarzschild's metric. The torsion tensor is calculated taking into account the non-symmetric part of the metric tensor in the vanishing of its covariant derivative and applied to Kerr's metric generalizing the Clifford algebra. Geodesic equation, conservation laws, torsion tensor and Einstein field equation are obtained in a non-symmetric geometry.
Schrödinger Equation; Gravitomagnetic Photon Emission; Gravitomagnetic Tensor; Gravitational Magnetic Field; Energy-Momentum 1-Form; Clifford Algebra; Dirac Equation; Dirac Operator; Gravity and Quantum Mechanics Unification; Multilevel Operator; Schwarzschild's Metric; Torsion Tensor; Rearranged Kerr's Metric; Generalized Dirac Equation; Generalized Clifford Algebra; Generalized Einstein Field Equation; Generalized Geodesic Equation; Conservation Laws; Non-Symmetric Geometry
Dirac's equation is the relativistic wave equation derived by physicist Paul Dirac in 1928. The wave functions in the Dirac theory are vectors of four complex components (known as bispinors), two of which resemble the Pauli wavefunction in the non-relativistic limit, in contrast to the Schrödinger equation which described wave functions of only one complex component.
Dirac's operator is just the tip of the iceberg, the tip of a generalized operator that is obtained by operating on all members of the Clifford algebra basis and not just on four of them.
The Schwarzschild's metric is named in honour of Karl Schwarzschild, who found the exact solution in 1915 and published it in January 1916, a little more than a month after the publication of Einstein's theory of general relativity. It was the first exact solution of the Einstein field equations other than the trivial at space solution. Schwarzschild died shortly after his paper was published, as a result of a disease he developed while serving in the German army during World War I. Johannes Droste in 1916 independently produced the same solution as Schwarzschild.
Schwarzschild's metric is an exact solution to the Einstein's field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constants are all zero.
The new generalized Dirac's operator, the multilevel operator, is calculated in the Schwarzschild's metric, torsion tensor and new gravitomagnetic tensor appear in level 2, curvature tensor appears in levels 3 and 4.
The Kerr's metric is a generalization to a rotating body of the Schwarzschild's metric. The Einstein field equation relates the geometry of spacetime to the distribution of matter within it. The equations were published by Einstein in 1915 in the form of a tensor equation which related the local spacetime curvature with the local energy, momentum and stress within that spacetime expressed by the stress-energy tensor.
An electron is orbiting a nucleus with Ζ protons, we know the energy levels from the solution of the Schrödinger equation [2], where mp is the proton mass, me is the electron mass, µ is the 2 -body reduced mass, e is the electron charge, ɼ is the position of the electron relative to the nucleus, the potential term is due to the Coulomb interaction wherein ∈0 is the permittivity of free space and mN is the mass of the nucleus.

(1)

(2)

(3)

(4)

(5)

(6)
with k = ke, now adding the gravitational potential  (7) And from equation (6)
(7) And from equation (6)

(8)

(9)

(10)

(11)

(12)

(13)

(14)
From equation (14)  is the frequency of the gravitomagnetic photon emitted from the initial energy level to the nal energy level. This emission leads us to the gravitomagnetic tensor. Gravitational magnetic eld generates the extra force needed to explain the anomalous behavior of pendulums observed during a solar eclipse, the Allais e ect [4] and also explains the dark matter e ect without exotic particles never detected. Gravitational magnetic eld is also derived from Special Relativity force transformations [5], when velocities point to the same direction a repulsive gravitational magnetic force is induced. Gravitomagnetic tensor will appear below in equation (44) at level two of the generalized Dirac equation D2
is the frequency of the gravitomagnetic photon emitted from the initial energy level to the nal energy level. This emission leads us to the gravitomagnetic tensor. Gravitational magnetic eld generates the extra force needed to explain the anomalous behavior of pendulums observed during a solar eclipse, the Allais e ect [4] and also explains the dark matter e ect without exotic particles never detected. Gravitational magnetic eld is also derived from Special Relativity force transformations [5], when velocities point to the same direction a repulsive gravitational magnetic force is induced. Gravitomagnetic tensor will appear below in equation (44) at level two of the generalized Dirac equation D2
From equation (13)  is the frequency of the electromagnetic photon emitted from the initial energy level to the nal energy level. The correction of the second term is an indirect detection of the gravitomagnetic photon emission
is the frequency of the electromagnetic photon emitted from the initial energy level to the nal energy level. The correction of the second term is an indirect detection of the gravitomagnetic photon emission

(15)

(16)
In equation (16) we have the energy levels from the solution of the Dirac's equation [3]. The first term is the solution of the Schrödinger equation that we have seen above in equation (6) and the second term is the relativistic correction.

(17)

(18)

(19)

(20)

(21)

(23)

(24)

(25)

(26)

(27)

(28)
From equation (27) is the relativistic correction of the electromagnetic photon emitted from the initial energy level to the final energy level and from equation (28)
is the relativistic correction of the electromagnetic photon emitted from the initial energy level to the final energy level and from equation (28)  is the relativistic correction of the gravitomagnetic photon emitted from the initial energy level to the final energy level.
is the relativistic correction of the gravitomagnetic photon emitted from the initial energy level to the final energy level.
We are using Pauli matrices σ, electromagnetic four-potential  and charge e with
and charge e with 

(29)
In four dimensions, Minkowski's metric  leads to the Clifford algebra
leads to the Clifford algebra  Dirac matrices
Dirac matrices 


(30)
Multilevel operator Dn acts on level n, n is the number of matrices in the product of the algebra members, for example, D3 acts on  . Total multilevel operator
. Total multilevel operator  = D0 +D1 +D2 +D3 +D4, the action of
= D0 +D1 +D2 +D3 +D4, the action of  on the spinor function vanishes
on the spinor function vanishes  (31)
(31)
 (32)
(32)
 (33)
(33)
 (34)
(34)
 (35)
(35)
 (36)
(36)
 (37)
(37)
Multilevel operator  can be generalized for a curved space with four-potential P, field charge q and covariant derivative[7] (;µ) instead of derivative (;µ) in the definition of pµ
can be generalized for a curved space with four-potential P, field charge q and covariant derivative[7] (;µ) instead of derivative (;µ) in the definition of pµ
 (38)
(38)
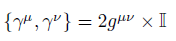 (39)
(39)
 (40)
(40)
 (41)
(41)
 (42)
(42)
 (43)
(43)
 (44)
(44)
 (45)
(45)
For gravity  (P) is the new gravitomagnetic tensor.
(P) is the new gravitomagnetic tensor.  is the torsion tensor [8]
is the torsion tensor [8]
 (46)
(46)
 (47)
(47)
 (48)
(48)
 (49)
(49)
 (50)
(50)
 (51)
(51)
We are using x
0= t,x
1 = r,x
2 = θ,x
3 = ϕ with G = c = 1, this metric is defined by [10]
 (52)
(52)
 (53)
(53)
 (54)
(54)
 (55)
(55)
 (56)
(56)
 (57)
(57)
 (58)
(58)
 (59)
(59)
 (60)
(60)
 (61)
(61)
 (62)
(62)
 (63)
(63)
 (64)
(64)
 (65)
(65)
 (66)
(66)
 (67)
(67)
 (68)
(68)
 (69)
(69)
 (70)
(70)


Energy-momentum form is a 1-form [11]
 (76)
(76)
dp is a 2 -form
 (77)
(77)


Comparing equations (69-71) and (78-80) we can infer
 (81)
(81)
D0 is related to the scalar 0 -form m, D1 is related to the Energy-momentum 1 -form, D2 is related to the Electromagnetic 2 -form, D3 is related to *J3-form [12]


Torsion Tensor in A Rearranged Kerr's Metric
We are using  is the black hole's mass and a is the angular momentum per unit mass with G = c = 1. The invariance of the length of vectors under parallel transport means that the connection is compatible with the metric, it is a metric connection, the requirement of the preservation of the length by parallel transport may be stated as [14]
is the black hole's mass and a is the angular momentum per unit mass with G = c = 1. The invariance of the length of vectors under parallel transport means that the connection is compatible with the metric, it is a metric connection, the requirement of the preservation of the length by parallel transport may be stated as [14]


Solving these equations we get the torsion applying its definition [15]
 (91)
(91)
Expanding the line element in powers of r-1 and examining the leading terms [16]

 (92)
(92)
Rearranging the line elements

 (93)
(93)


 (106)
(106)
Generalizing Clifford algebra with 


 (114)
(114)
 (115)
(115)
 (116)
(116)
 (117)
(117)
 (118)
(118)


 (119)
(119)
A geodesic that is not a null geodesic has the property that ∫ ds, taken along a section of the track with the end points P and Q, is stationary if one makes a small variation of the track keeping the end points fixed. If dx μ denotes an element along the track [17]


By partial integration with  at end points P and Q, we get
at end points P and Q, we get
 (125)
(125)
The condition for this to vanish with arbitrary  is
is


From equation (126) with 
 (130)
(130)
Thus the condition (102) becomes


Multiplying equation (131) by  , we obtain the geodesic equation
, we obtain the geodesic equation


 are the Christoffel symbols of the symmetric part, so
are the Christoffel symbols of the symmetric part, so
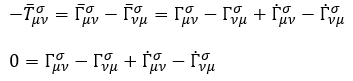

We directly obtain the torsion tensor without solving equations (90) and (91)
 (139)
(139)
From equation (136) where  are the symbols of the symmetric part
are the symbols of the symmetric part


Equation (140) becomes


The vector A μ has the covariant divergence


If the left-hand side of equation (147) equals zero then the right-hand side gives us the first conservation law.
For the antisymmetric tensor 


If the left-hand side of equation (150) equals zero then the right-hand side gives us the second conservation law.
For the antisymmetric tensor 


Adding equations (152), (153) and (154)
 (155)
(155)
From the definition of the curvature tensor 
 (156)
(156)
 is called the Ricci tensor
is called the Ricci tensor
 (157)
(157)
Now  is not symmetric,
is not symmetric,  is the antisymmetric part and
is the antisymmetric part and  is the symmetric part in the Einstein's equation [18].
is the symmetric part in the Einstein's equation [18].
 (158)
(158)

 (159)
(159)


Multilevel operator  has been generalized for a curved space with a general four-potential P. For gravity
has been generalized for a curved space with a general four-potential P. For gravity  is the new gravitomagnetic tensor and torsion tensor
is the new gravitomagnetic tensor and torsion tensor  appears in its definition
appears in its definition
In a flat space  and D4 operators vanish. In a curved space the curvature tensor
and D4 operators vanish. In a curved space the curvature tensor  appears in levels 3 and 4
appears in levels 3 and 4
The appearance of torsion tensor  and curvature tensor
and curvature tensor  in multilevel operator
in multilevel operator  means that this operator is a fundamental operator in Quantum Field Theory
means that this operator is a fundamental operator in Quantum Field Theory
 , have been calculated for Schwarzschild's metric, then
, have been calculated for Schwarzschild's metric, then  , the gravitomagnetic tensor has been obtained
, the gravitomagnetic tensor has been obtained
Each Dn, where n is the number of ϒ matrices in the product of the algebra members, is related to an n-form
The invariance of the length of vectors under parallel transport requires the vanishing of the metric tensor covariant derivative, a new term appears in equation (87) with  measuring the non symmetric part of the metric tensor, solving these equations we get the torsion tensor
measuring the non symmetric part of the metric tensor, solving these equations we get the torsion tensor
Rearranging Kerr's metric we obtained  , the non symmetric part of the metric tensor, gravitomagnetic tensor has also been calculated generalizing the Clifford algebra
, the non symmetric part of the metric tensor, gravitomagnetic tensor has also been calculated generalizing the Clifford algebra
Taking into account the  in the geodesic equation we have obtained the torsion tensor, conservation laws and Einstein field equation in a non-symmetric geometry
in the geodesic equation we have obtained the torsion tensor, conservation laws and Einstein field equation in a non-symmetric geometry
The solution of the Schrödinger's equation leads us to the emission of gravitomagnetic photons when the gravitational potential is also taken into account. The correction of the second term in electromagnetic photon frequency is an indirect detection of the gravitomagnetic photon emission.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 637.
- Robert Eisberg., Robert Resnick (1979) Fisica Cuantica. Atomos, moleculas, solidos, nucleos y particulas. Editorial Limusa 286.
- Robert Eisberg., Robert Resnick (1979) Fisica Cuantica. Atomos, moleculas, solidos, nucleos y particulas. Editorial Limusa 337.
- Delso J (2022) On Allais effect explained by the Gravitomagnetic tensor. OSP Journal of Physics and Astronomy 3.
- Delso J (2021) On Gravitational Magnetic Field Derived from Special Relativity Leading to Dark Matter Force. OSP Journal of Physics Astronomy 2.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 650-652.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 380.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 384.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 404.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University 30-32.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 91.
- Roger Penrose (2006) El camino a la realidad. Random House Mondadori 603.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 119.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University 383.
- Marian Fecko (2006) Differential Geometry and Lie Groups for Physicists. Cambridge University Press 389.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 891.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University 16-17.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 406.
