Kepler’s third law states that the square of the period of the orbit of a planet about the Sun is proportional to the cube of the semi-major axis of the orbit, now this law is derived from Schrodinger's equation applied to a gravitational system. Mercury deviates from the precession predicted from the Newtonian effects. In general relativity, this remaining precession, or change of orientation of the orbital ellipse within its orbital plane, is explained by gravitation being mediated by the curvature of spacetime. Einstein showed that general relativity agrees closely with the observed amount of perihelion shift. This was a powerful factor motivating the adoption of general relativity. Now this effect is also explained by the action of the gravitational magnetic field.
Kepler's Third Law; Schrodinger's Equation; Perihelion Precession; Gravitomagnetic Tensor; Gravitational Magnetic Field; Energy-Momentum 1-Form; Gravitomagnetic Photon Emission; Maxwell's Equations; Planck's Constant; Planck's Constant Variation; Gravity and Quantum Mechanics Unification
The gravitomagnetic photon emission is the first step to get a new Astronomy, it is derived from the solution of Schrodinger's equation adding the gravitational potential. The variation in Planck's constant is the first step to get the Gravity and Quantum Mechanics unification, the variation is derived from the solution of Schrodinger's equation in gravitational systems [1].
Electromagnetic tensor is a 2-form derived from the exterior derivative of a 1-form, similarly Gravitomagnetic tensor [2] can be derived from the exterior derivative of the Energy-momentum 1-form and we obtain the similar Maxwell's equations.
Gravitomagnetic tensor [2] generates the extra force needed to explain the anomalous behavior of pendulums observed during a solar eclipse [3] and dark matter effect.
Solving the Schrodinger's equation with the gravitational potential added to the electrical potential we are able to get the gravitomagnetic photon frequency.
Equating the Schrodinger's energy value to the total energy in several gravitational systems we get the value of Planck's constant in these systems.
There must be a precession of the angular momentum around the gravitational magnetic field created by the planet orbiting the star.
Electromagnetic form is a 2-form [4].
F = −Exdt ∧ dx − Ey dt ∧ dy − Ez dt ∧ dz + Bxdy ∧ dz + By dz ∧ dx + Bz dx ∧ dy (1)
Energy-momentum form is a 1-form [4].
p = −Edt + pxdx + pydy + pzdz (2)
Gravitomagnetic form is a 2-form
G = dp = −Exdt ∧ dx − Ey dt ∧ dy − Ez dt ∧ dz + Bxdy ∧ dz + By dz ∧ dx + Bz dx ∧ dy (3)
G01 = −Ex = px,t + E,x (4)
G02 = −Ey = py,t + E,y (5)
G03 = −Ez = pz,t + E,z (6)
G23 = Bx = pz,y − py,z (7)
G31 = By = px,z − pz,x (8)
G12 = Bz = py,x − px,y (9)
dG = ddp = 0 [5], we obtain the similar Maxwell's equations
Div B = 0 (10)
Curl E = –B,t (11)
*is the Hodge dual [5].
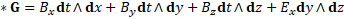
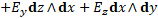 (12)
(12)
d* G=4π* J [5], we obtain the last 2 equations with ρ, the mass density
Div E = 4πρ (13)
Curl B = E,t + 4πJ (14)
where E ρσ is the stress-energy tensor of the field.
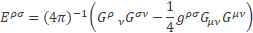 (15)
(15)
An electron is orbiting a nucleus with Z protons, we know the energy levels from the solution of the Schr odinger's equation[6], where mp is the proton mass, me is the electron mass, μ is the 2-body reduced mass, e is the electron charge, r is the position of the electron relative to the nucleus, the potential term is due to the Coulomb interaction wherein ∈0 is the permittivity of free space and mN is the mass of the nucleus.
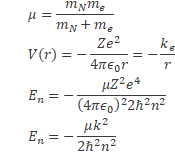
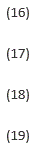
with κ = κ e' now adding the gravitational potential
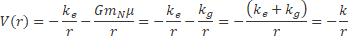 (20)
(20)
And from equation (19)
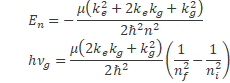

For the hydrogen atom, Z = 1, the first term in equation (21) is -13.6 eV, the third term is due to the gravitational interaction and the second term is due to the fact that the electron is closer to the nucleus than it would be without the electromagnetic interaction.
We apply equation (21) to the Sun-Earth system, equating equation (21) to the total energy of the gravitational system we get the value of Planck's constant in this system, Ms = 1:9885 _ 1030kg is the Sun mass, Me = 5:97237 _ 1024kg is the Earth mass, a = 149598023000m is the semi-major axis, eccentricity ex = 0:0167086, kg = GMs μ, n = l + 1 and L the angular momentum.
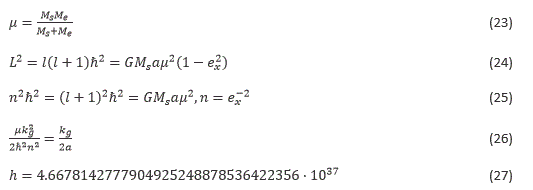
We apply equation (21) to the Sun-Jupiter system, Ms = 1:9885.1030kg is the Sun mass, Mj = 1:8982.1027kg is the Jupiter mass, a = 778:57.109m is the semi-major axis, eccentricity ex = 0:0489, kg = GMsμ and n = e x-2 = 419

An electron is orbiting a nucleus with Z protons, me is the electron mass, μ is the 2-body reduced mass, e is the electron charge, r is the position of the electron relative to the nucleus, the potential term is due to the Coulomb interaction wherein ∈0 is the permittivity of free space, the magnetic field B created by the electron motion is defined by [7].
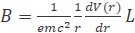 (31)
(31)
the angular frequency of precession is defined by [8].
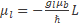 (32)
(32)
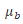 is the Bohr magneton defined by
is the Bohr magneton defined by
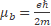 (33)
(33)
Adapting equations (31) (32) (33) to a gravitational system
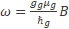 (34)
(34)
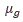 is the gravitational magneton defined by
is the gravitational magneton defined by
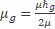 (35)
(35)
B is the gravitational magnetic field where V(r) is the gravitational potential
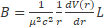 (36)
(36)
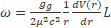 (37)
(37)
T is the period from the Kepler's third law
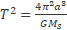 (38)
(38)
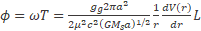 (39)
(39)
and bringing L value from equation (24)

and Φ value from equation (40)
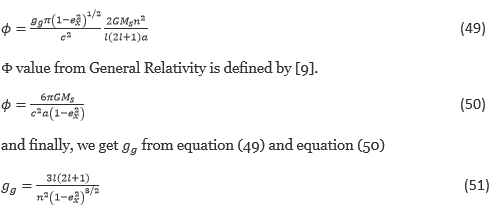
We apply equation (51) to the Sun-Mercury system with eccentricity 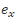 = 0:205630 and
= 0:205630 and 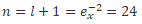
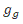 =6.0071592409034304 (52)
=6.0071592409034304 (52)
We apply equation (51) to the Sun-Mars system with eccentricity  = 0:093315 and
= 0:093315 and 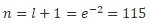
 =6.0001664944193108 (53)
=6.0001664944193108 (53)
We apply equation (51) to the Sun-Saturn system with eccentricity 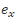 = 0:05648 and
= 0:05648 and 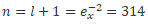
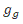 =6.0000552764267231 (54)
=6.0000552764267231 (54)
We apply equation (51) to the Sun-Jupiter system with eccentricity 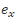 = 0:0489 and
= 0:0489 and 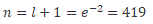
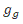 =6.0000455574084054 (55)
=6.0000455574084054 (55)
We apply equation (51) to the Sun-Earth system with eccentricity 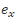 = 0:0167086 and
= 0:0167086 and 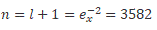
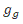 =6.0000000914905551 (56)
=6.0000000914905551 (56)
We apply equation (51) to the Sun-Neptune system with eccentricity 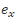 = 0:008678 and
= 0:008678 and 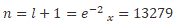
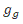 =6.0000000115305529 (57)
=6.0000000115305529 (57)
We apply equation (51) to the Sun-Venus system with eccentricity 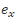 = 0:00677323 and
= 0:00677323 and 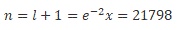
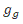 =6.0000000094647978 (58)
=6.0000000094647978 (58)
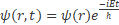 (59)
(59)
T is the period and Kepler's third law is defined by
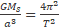 (60)
(60)
E is the total Energy in a gravitational system defined by
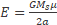 (61)
(61)
From equation (25)
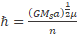 (62)
(62)
and
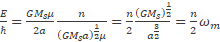 (63)
(63)
ωm is the mean motion angular speed defined by
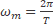 (64)
(64)
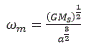 (65)
(65)
equations (64) and (65) define Kepler's third law and
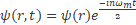 (66)
(66)
Mean motion angular speed ωm for our planets:

(67)

(68)
Mean motion angular speed ωm for planets in Proxima Centauri:
 (69)
(69)
(70)
Comparing equations (68) and (70) we see a gap for 5 planets from! ωm1 / ωm3 to ωm1 / ωm7
Gravitomagnetic tensor has been derived from the Energymomentum and we have obtained the similar Maxwell's equations, when a charged particle is moving it generates a magnetic field that interacts with charged particles in motion, similarly when a particle is moving it generates a gravitational magnetic field that interacts with other particles in motion.
Gravitomagnetic photon frequency  is obtained by solving the Schrodinger's equation including the gravitational potential, the detection of this photon leads to a new Astronomy.
is obtained by solving the Schrodinger's equation including the gravitational potential, the detection of this photon leads to a new Astronomy.
The variation in Planck's constant is obtained by solving the Schrodinger's equation in several gravitational sys- tems, it is not a constant anymore, it depends on the masses, the semi-major axis and quantum number  .
.
Galaxies in our universe are rotating with such speed that the gravity generated by their observable matter could not possibly hold them together. Gravitomagnetic tensor and the interaction due to the torsion tensor explain dark matter, the shape of galaxies and their distribution in the universe.
Gravitational magnetic force explains the Allais effect and other anomalies such as that of the Pioneer spacecraft and its acceleration when moving away from the Sun.
The precession of the angular momentum around the gravitational magnetic field explains the perihelion precession and has been calculated for the planets of the solar system.
Kepler's third law is derived from Schrodinger's equation and confirms that it is correct to apply Schrodinger's formalism to a gravitational system with the condition n = 1 + 1.
Five new planets have been predicted, comparing the mean motion angular speed ratios between our planetary system and Proxima Centauri system.
- Delso J (2022) On Gravitomagnetic Photon Emission and Variation in Planck Constant. OSP Journal of Physics and Astronomy 3: 129.
- Delso J (2022) On Gravitomagnetic Tensor Derived from Energy Momentum 1-Form in a Riemann-Cartan Space with a Metric Connection. OSP Journal of Physics and Astronomy 3: 126.
- Delso J (2022) On Allais effect explained by the Gravitomagnetic tensor. OSP Journal of Physics and Astronomy 3: 127.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 91.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University 113.
- Robert Eisberg., Robert Resnick (1979) Fisica Cuantica. Atomos, moleculas, solidos, nucleos y particulas. Editorial Limusa 286.
- Robert Eisberg., Robert Resnick (1979) Fisica Cuantica. Atomos, moleculas, solidos, nucleos y particulas. Editorial Limusa 330.
- Robert Eisberg., Robert Resnick (1979) Fisica Cuantica. Atomos, moleculas, solidos, nucleos y particulas. Editorial Limusa 320.
- Hermann Weyl (1952) Space, time, matter. Dover Publications Inc 258. Robert Eisberg., Robert Resnick (1979) Fisica Cuantica. Atomos, moleculas,
- solidos, nucleos y particulas. Editorial Limusa 281.

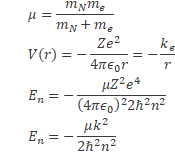
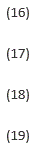
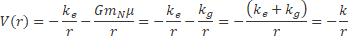 (20)
(20)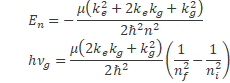

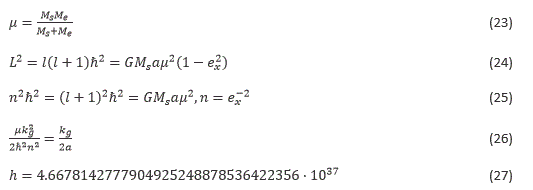

 (31)
(31)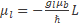 (32)
(32)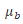 is the Bohr magneton defined by
is the Bohr magneton defined by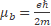 (33)
(33)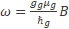 (34)
(34)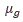 is the gravitational magneton defined by
is the gravitational magneton defined by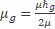 (35)
(35)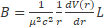 (36)
(36)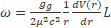 (37)
(37)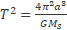 (38)
(38)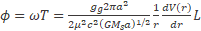 (39)
(39)
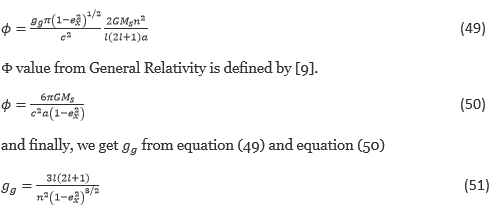
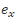 = 0:205630 and
= 0:205630 and 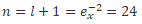
 =6.0071592409034304 (52)
=6.0071592409034304 (52)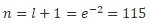
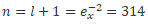
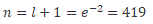
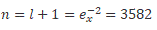
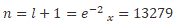
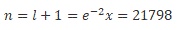
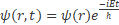 (59)
(59)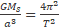 (60)
(60)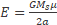 (61)
(61)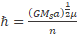 (62)
(62)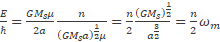 (63)
(63)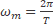 (64)
(64)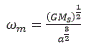 (65)
(65)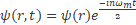 (66)
(66)

 (69)
(69)