Poynting vector, Maxwell stress tensor and Lorentz force are generalized in curved space derived from gravitomagnetic tensor.
Gravitomagnetic tensor is derived from General Relativity comparing the action for a continuous distribution of matter and the action for the electromagnetic field.
Gravitational magnetic force is also derived from Special Relativity force transformations. Similarly to the spin-orbit interaction there is magnetic field acting on the star S2 induced by the supermassive black hole gravitational field.
Energy tensors are defined to complete the General Relativity field equations. Ricci decomposition is a way of breaking up the Riemann curvature tensor into three orthogonal tensors, Z, Weyl tensor C and S.
Poynting Vector; Maxwell Stress Tensor; Lorentz Force; Curved Space; Gravitomagnetic Tensor; General Relativity; Dark Matter; Expansion of the Universe; Riemann Curvature; Ricci Decomposition; Special Relativity; Gravitational Magnetic Field; Gravitational Magnetic Force; Star S2; Galactic Center Supermassive Black Hole; General Relativity Field Equations
Galaxies in our universe are rotating with such speed that the gravity generated by their observable matter could not possibly hold them together; an extra force is needed to explain it.
Gravitational magnetic force is a relativistic force derived from Special Relativity force transformations. Gravitational magnetic force acting on the star S2 induced by the supermassive black hole gravitational field is calculated.
Gravitomagnetic tensor is derived from General Relativity comparing the similarities between the matter action and the electromagnetic field action; there must be similar expressions for Poynting vector, Maxwell stress tensor and Lorentz force in curved space confirming the gravitomagnetic tensor existence.
Poynting Vector, Maxwell Stress Tensor and Lorentz Force in Curved Space
The six components of the antisymmetric tensor 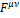 determine the field quantities E and H [17].
determine the field quantities E and H [17].
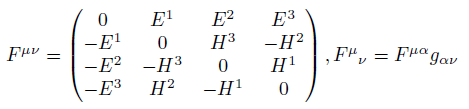 (1)
(1)
Gravitomagnetic tensor is defined by [18].
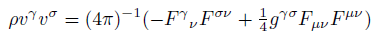 (2)
(2)
We form the four-vector 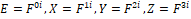 and define "component (i)"
and define "component (i)"
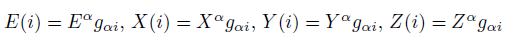 (3)
(3)
Poynting vector components in curved space
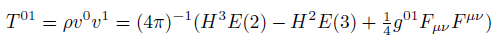 (4)
(4)
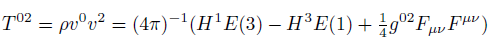 (5)
(5)
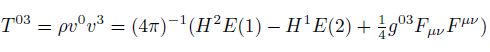 (6)
(6)
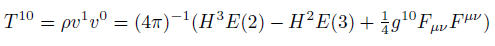 (7)
(7)
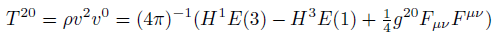 (8)
(8)
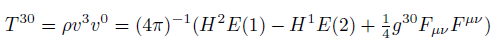 (9)
(9)
Maxwell stress tensor components in curved space.
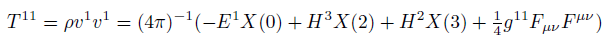 (10)
(10)
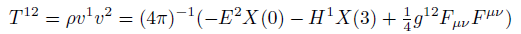 (11)
(11)
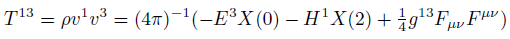 (12)
(12)
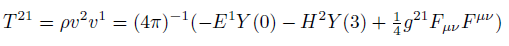 (13)
(13)
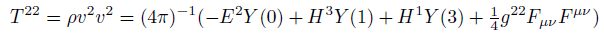 (14)
(14)
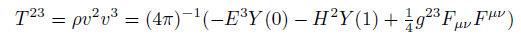 (15)
(15)
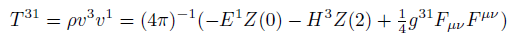 (16)
(16)
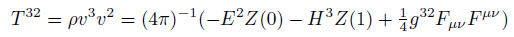 (17)
(17)
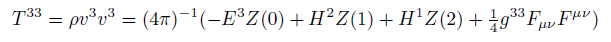 (18)
(18)
Energy density component in curved space.
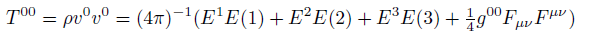 (19)
(19)
From symmetric stress-energy tensor T in flat space [19].
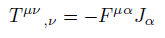 (20)
(20)
Lorentz 4-force in flat space [20].
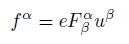 (21)
(21)
From symmetric stress-energy tensor T in curved space [21].
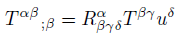 (22)
(22)
Similarly gravitomagnetic 4-force in curved space.
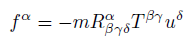 (23)
(23)
We shall consider a continuous distribution of matter whose velocity varies continuously from one point to the neighbouring one. We shall set up an action principle for this matter in interaction with the gravitational field in the form [14].
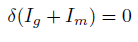 (24)
(24)
where Ig is the gravitational part of the action and Im is the matter part of the action [15].
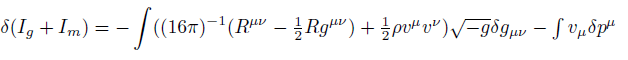 (25)
(25)
and for Iem, the electromagnetic field action, we get for the total variation [16].
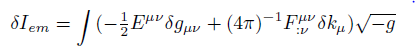 (26)
(26)
where 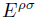 is the stress-energy tensor of the electromagnetic field [16].
is the stress-energy tensor of the electromagnetic field [16].
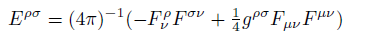 (27)
(27)
Comparing equations (25) and (26) is evident that gravitomagnetic tensor is defined by
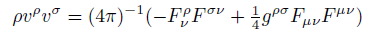 (28)
(28)
Gravitational Magnetic Force on the Star S2 Orbiting the Galactic Center Supermassive Black Hole
In quantum physics, in the spin-orbit interaction there is a magnetic field B acting on the electron in the rest frame of the electron, where v is the velocity of the electron and E is the electric field, in the non-relativistic limit, 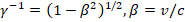 , the speed of light,
, the speed of light, 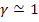 [11].
[11].
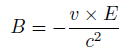 (29)
(29)
A particle without electric charge (q = 0) and rest mass m0 is orbiting a gravitational source with rest mass M0; m0 << M0, and velocity v at its closest approach distance r, since q = 0 the only force is the gravitational force.
The gravitational magnetic field is derived from Special Relativity force transformations [12], when velocities point to the same direction a repulsive gravitational magnetic force is induced FBg,
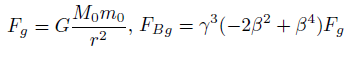 (30)
(30)
When velocities point to the opposite direction an attractive gravitational magnetic force is induced FBg.
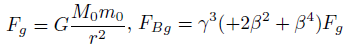 (31)
(31)
So, with v = 7650 km/s, r = 120 AU, M0 = 4.31 million Mo, m0 = 10 Mo, [13] we obtain the FBg value on the star S2 orbiting the Galactic center supermassive black hole at its closest approach.
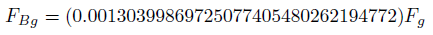 (32)
(32)
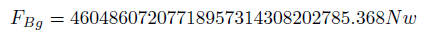 (33)
(33)
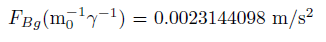 (34)
(34)
FBg is an extra attractive gravitational magnetic force pulling from the star; however this force is attributed to exotic particles never detected. You can also see discussions about dark matter and the expansion of the universe in [10].
Conformal energy U defined as a combination of C and the Hodge dual of C, energy D tensor defined as a combination of S and the Hodge dual of S, similar definitions for V/Z and T/R
The Ricci decomposition is a way of breaking up the Riemann curvature tensor into three orthogonal tensors, Z, Weyl tensor C and S, S tensor [6-8].
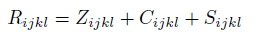 (35)
(35)
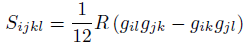 (36)
(36)
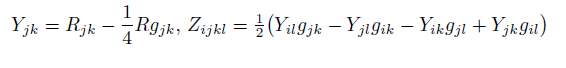 (37)
(37)
where Rabcd is the Riemann tensor, Rab is the Ricci tensor, R is the Ricci scalar (the scalar curvature).
The conformal energy tensor U can be defined as a combination of C and the Hodge dual of C [1-3].
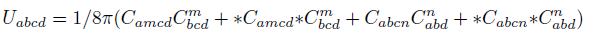 (38)
(38)
The new energy tensor D can be defined as a combination of S and the Hodge dual of S.
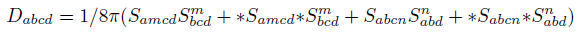 (39)
(39)
The new energy tensor V can be defined as a combination of Z and the Hodge dual of Z.
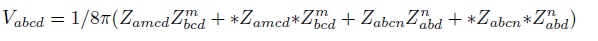 (40)
(40)
The new Total Energy tensor T can be defined as a combination of the Riemann tensor R and the Hodge dual of R
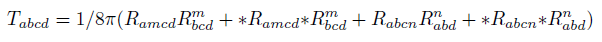 (41)
(41)
The Hodge dual definition for Electromagnetic tensor and Weyl tensor [4].
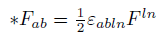 (42)
(42)
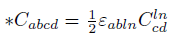 (43)
(43)
The Hodge dual definition for S, Z and R tensors
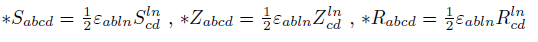 (44)
(44)
Weyl tensor C (4, 0) is related to the new Conformal Energy tensor U (4, 0). Tensor S (4, 0) is related to the new energy tensor D (4, 0). Z (4, 0) tensor is related to the new energy tensor V (4, 0). Riemann tensor R (4, 0) is related to the new Total Energy tensor T (4, 0).
The complete field equations are described by a new T (4, 0) tensor for Total Energy, the new conformal energy tensor U (4, 0), the new energy tensor V (4, 0) and the new energy tensor D (4, 0).
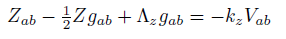 (45)
(45)
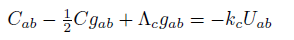 (46)
(46)
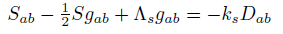 (47)
(47)
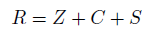 (48)
(48)
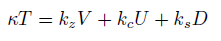 (49)
(49)
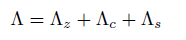 (50)
(50)
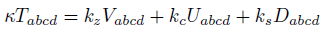 (51)
(51)
In the general theory of relativity the Einstein field equations relate the geometry of spacetime to the distribution of matter [5].
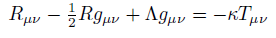 (52)
(52)
Poynting vector, Maxwell stress tensor and Lorentz force have been generalized in curved space confirming the gravitomagnetic tensor, electromagnetic Poynting vector, Maxwell stress tensor and Lorentz force are the special case defined in flat space with Minkowski metric.
Gravitomagnetic tensor leads to gravitomagnetic waves and the gravitational magnetic force, gravitomagnetic waves will be detected in the future opening a new Astronomy.
The maximum acceleration on the star S2 due to the magnetic gravitational force is 0.0023144098 at its closest approach, the supermassive black hole gravitational field is inducing an extra attractive gravitational magnetic force pulling from the star, and however this force is attributed to exotic particles never detected.
When a charged particle is moving it generates a magnetic field that interacts with charged particles in motion, similarly when a particle with mass is moving it generates a gravitational magnetic field that interacts with other particles in motion.
This new force, gravitational magnetic force, has been detected by astronomers for decades but has been misinterpreted, in a galaxy there are no dark matter particles generating the dark matter force, moving stars generate gravitational magnetic fields that interact with other stars in motion.
Gravitational magnetic force also defines the distribution of galaxies in the universe.
Gravitational magnetic force is also derived from Special Relativity force transformations; if Special Relativity is correct then gravitational magnetic force is irrefutable.
- Jesus Delso Lapuerta (2020) On the conformal energy tensor defined as a combination of Weyl tensor and the Hodge dual of Weyl tensor. Vixra.org Relativity and Cosmology 2-3.
- Roger Penrose (2006) El camino a la realidad" Random House Mondadori, Barcelona 619.
- Roger Penrose (2006) El camino a la realidad" Random House Mondadori, Barcelona 629.
- Roger Penrose (2006) El camino a la realidad Random House Mondadori, Barcelona 1255.
- Albert Einstein (1985) El significado de la relatividad" Planeta - De Agostini, Barcelona 175.
- Besse, Arthur L (1987) Einstein manifolds, Ergebnisse der Mathematik undihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)]10 Berlin, New York: Springer-Verlag, pp. xii+510.
- Sharpe, R.W (1997) Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer-Verlag, New York, Section 6.1 discusses the decomposition. Versions of the decomposition also enter into the discussion of conformal and projective geometries, in chapters 7 and 8.
- Singer, I.M., Thorpe, J.A (1969) The curvature of 4-dimensional Einstein spaces, Global Analysis (Papers in Honor of K. Kodaira), Univ. Tokyo Press 355-365.
- Robert Resnick (1977) Introduccion a la Teoria Especial de la Relatividad" Editorial Limmusa, Mexico DF139.
- Delso J (2021) On Dark Matter Gravity Force Generated by the Expansion of the Universe. OSP Journal of Physics and Astronomy 2: JPA-2-111.
- Robert Eisberg., Robert Resnick (1979) Fisica Cuantica. Atomos, moleculas, solidos, nucleos y particulas. Editorial Limmusa, Mexico DF 329.
- Delso J (2021) On Gravitational Magnetic Field Derived from Special Relativity Leading to Dark Matter Force. OSP Journal of Physics and Astronomy 2: JPA-2-115.
- Wikipedia (2021) S2 (star). wikipedia.org.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 50.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 53.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 54-55.
- P.A.M. Dirac (1996) General Theory of Relativity. Princeton University Press 42.
- Delso J (2021) On Gravitomagnetic Tensor Derived From General Relativity. OSP Journal of Physics and Astronomy 2: JPA-2-120.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation Princeton University Press 89.
- J.A. Wheeler., C. Misner, K.S. Thorne (2017) Gravitation Princeton University Press 73.
- J.A. Wheeler., C. Misner, K.S. Thorne (2017) Gravitation Princeton University Press 390.

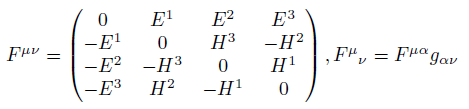 (1)
(1)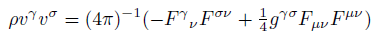 (2)
(2)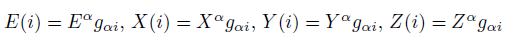 (3)
(3)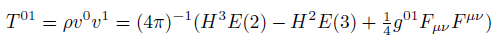 (4)
(4)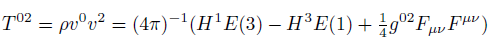 (5)
(5)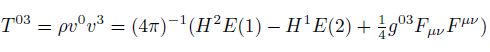 (6)
(6)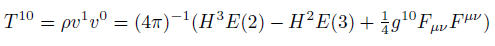 (7)
(7)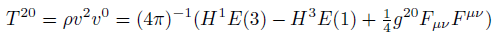 (8)
(8)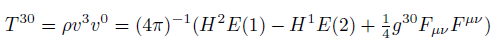 (9)
(9)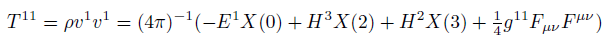 (10)
(10)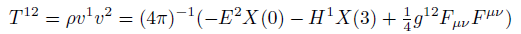 (11)
(11)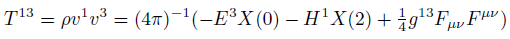 (12)
(12)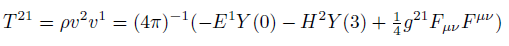 (13)
(13)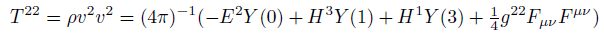 (14)
(14)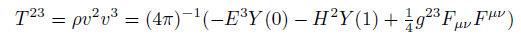 (15)
(15)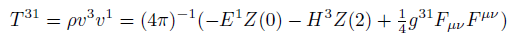 (16)
(16)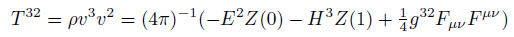 (17)
(17)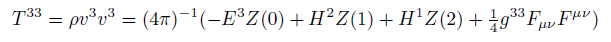 (18)
(18)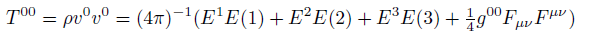 (19)
(19)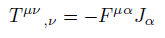 (20)
(20)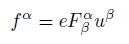 (21)
(21)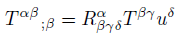 (22)
(22)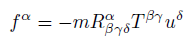 (23)
(23)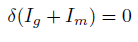 (24)
(24)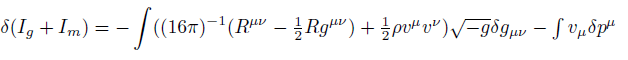 (25)
(25)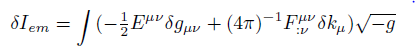 (26)
(26)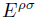 is the stress-energy tensor of the electromagnetic field [16].
is the stress-energy tensor of the electromagnetic field [16].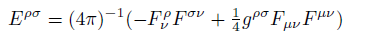 (27)
(27)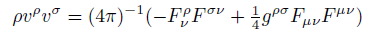 (28)
(28)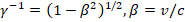 , the speed of light,
, the speed of light, 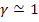 [11].
[11].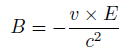 (29)
(29)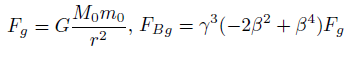 (30)
(30)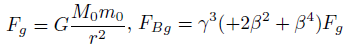 (31)
(31)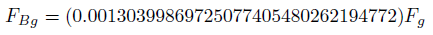 (32)
(32)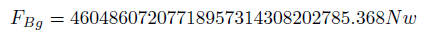 (33)
(33)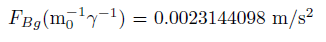 (34)
(34)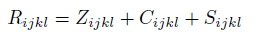 (35)
(35)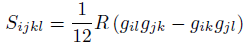 (36)
(36)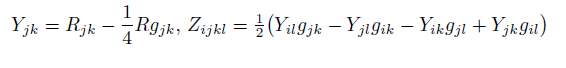 (37)
(37)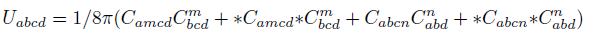 (38)
(38)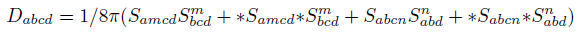 (39)
(39)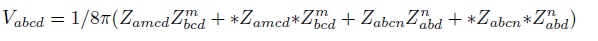 (40)
(40)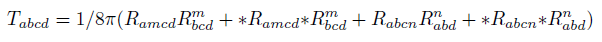 (41)
(41)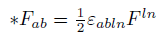 (42)
(42)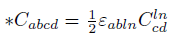 (43)
(43)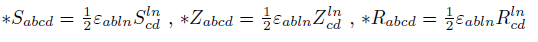 (44)
(44)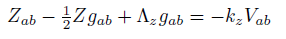 (45)
(45)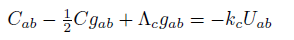 (46)
(46)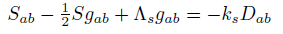 (47)
(47)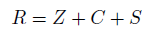 (48)
(48)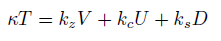 (49)
(49)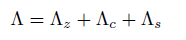 (50)
(50)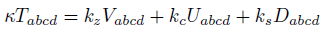 (51)
(51)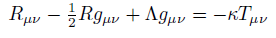 (52)
(52)