Abstract

If rapid motion is added to the Earth in the form of a redshift (3.14) due to the expansion of space, which complements the notion of an expanding universe, this information can be used to calculate both distances and time periods. If an accelerated system and a gravitational field coexist, a ‘short evolutionary distance’ (h) can be computed that points toward the origin of the universe. From this value, the knowledge of the total plane angle (2∙π) and the deflection angle (α) of the light beam grazing on the Earth's surface makes it possible to determine huge distances using the rules of trigonometry (H_universe=h∙2∙π/α). This ‘long evolving distance’ in the radius range of the universe can be converted to ‘evolving time’ (T_universe) if divided by the speed of light (c). Utilizing the inverse ratio of the angles (1/2 ∙α/π), the size of the Earth is the same as known. In the possession of the geometrically related components of the equation, further statements about the shape and structure of the cosmos and the Earth can be made. The time interval required for the formation of the entire Solar System and the Earth within it, derived from the cosmos age using the principle of symmetry and the value of π, is approximately 4.65 billion years and for our planet 4.53 billion years.

Key Words

Cosmological Parameters; High Redshift Galaxies; Earth; Gravitation; General Relativity; Euclidean Geometry; Gravitational Lensing; Radiometric Dating; Shape and Structure of the Universe; Age of the Earth and the Solar System

1. Introduction

According to the concept of an expanding universe [1], in which each galaxy moves away from each other, the past point at which the universe was created can be calculated [2]. Consequently, the same dynamics apply to the Milky Way, including the Earth. If the motion due to the rapid expansion of space [3] is applied to Earth, the planet together with its gravitational field forms a threedimensional expansion sphere. This situation results in a beam of light passing through the Earth’s gravitational field propagating in a homogeneous gravity for a long time, the recognition of which creates new possibilities for determining the various physical parameters of the universe [4]. Therefore, these tools can be used to calculate when the universe and the Solar System including the Earth were created. Using the general theory of relativity [5] and the rules of Euclidean geometry, an alternative method of dating can also be designed.

2. Method: Distance Determination

This essentially triangular distance determination method is similar to length determinations based on the gravitational lens effect [6]. In this case, the significant curvature of light continuously traveling along the moving Earth corresponds to the light deflection of massive celestial bodies (galaxy clusters). The magnifying effect is achieved from the direction of the infinitely small angle of curvature of the light beam passing by the quasi-static Earth. Then the short evolving distance (hpast present) formed by the multiplied mass of the Earth coincides with the radius (Huniverse) of the cosmos defining it (Figure 1).

3. Determining the Radius of the Universe From the Aspect of the High Redshift Milky Way Galaxy Including the Earth, in the Expanding Cosmos

Since there also exists time shift behind redshift [5] it is possible to calculate the exact point in time due to the rapid expansion of space in a manner to estimate the time interval involved by invoking the basic laws of physics.

3.1 Relationship between light frequency shift and distance in Earth's gravity

Alterations in either the acceleration or the gravitational fields (or both together) result in changes regarding the frequency of light. This shift of the spectrum line to a lower frequency is demonstrated by Einstein’s original formula [7].

Where, ν is the altered frequency, ν_o is the initial frequency, c is the speed of light and Φ is the gravitation potential difference.

The gravitational potential difference (Φ) is equal to the product of free fall acceleration (g) and the distance (h) between two points of different gravitational potentials: Φ=g.h [7]. Therefore:

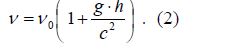
If the same extent of a light beam’s redshift measured at farther galaxies [8] is equated to the acceleration of the Earth (as a component of our galaxy) the above formula may also be applied. (Ignoring the rotation of the Solar System compared to the center of the Milky Way /v ≈ 2.3∙10⁵ m∙s^-1 / and the Earth's orbit around the Sun /v ≈ 3∙10⁴ m∙s^-1/ in this situation. This is because their magnitude cannot be compared to the expansion of space between distant galaxies [9] that reach the speed of light.) In this manner, a distance (h) can be calculated pointing towards the origin of the universe. This ‘short evolving distance’ (h_{past present in g}) from a physical point of view is:

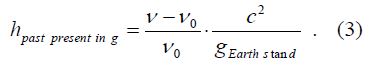
Where h_{past present in g} is the unknown distance between two points of a gravitational field, (ν-ν_ο)/ν_ο= 3.141592653 is the redshift of the Earth as a component of the highly redshifted Milky Way Galaxy. The c is the speed of light (2.99792458·10⁸ m·s^-1) [10] and g is the standard gravity of the Earth (9.80665 m·s^-2) [11].

Numerically:

This distance (Eq. 3.a) depends on both the spectrum line shift ratio, which matches the motion of the Earth, and the gravity of the Earth (Figure 1.a).

3.2 The degree of light deflection in the case of the Earth

The deviation angle of a light beam (α_{Earth in g}) passing near to a celestial body’s surface (in this case that of the Earth) is, according to Einstein’s formula [7].

Numerically:

Consequently, a miniscule deflection angle of α_Earth of any light beam passing by the Earth should be multiplied by the enormous value of 2∙π∙α^-1 (4.513249028·10⁹) to create a complete angle of 2∙π.

The ‘short evolving distance’ (h_{past present in g}) can be given mathematically or geometrically by the ratio of the entire plane angle (2∙π) and the deviation angle (α_{Earth in g}) of a light beam passing near the Earth’s surface caused by the gravitational field [12].

With the ratio calculated from the known ‘short evolving distance’ (h_{past present in g}) and the two known angles (α_{Earth in g}, 2∙π) an enormous unknown distance can be calculated, which might be termed the ‘long evolving distance’ (H_{universe past present in non-g} = R_universe) (Figure 1.b).

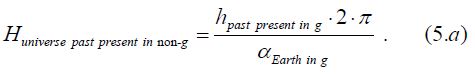
3.3 The relationship between light frequency shift and light curvature in variable (dynamic and static) Earth-surface gravity

Therefore, by conjoining the two original Einstein equations (Eq.1 and Eq.4) describing redshift and deflection of light, using the ratio of 2∙π/α, the following unified equation can be obtained:​

Where, H_{universe past present in non-g} is the radius of the universe, (ν-ν_o)/ν_o = 3.141592653 is the redshift of the Earth (as a component of the highly redshifted Milky Way Galaxy), c is the speed of light (2.99792458·10⁸ m·s^-1), π is the ratio of a circle’s circumference to its diameter (3.141592653). G is the gravitational constant (6.673848·10^-11 m³·kg^-1·s^-2) [10], R is the volumetric mean radius of the Earth (6.371005·10⁶ m), g is the standard gravity of the Earth (9.80665 m·s^-2). M is the mass of the Earth (5.97219·10²⁴ kg) [11] and α’_{Earth in non-g} is the vertically opposite angle of α_{Earth in g} (the two angles to be equal in the classical geometric sense).

When considering the large redshift /(ν-ν_o)/ν_o = 3.141592/ which may be measured from stars farther away [13], the ‘long evolving distance’ equals approximately 13·10²⁵ m, the radius of the universe (H_{universe past present in non-g}):

According to them, the concrete result is as follows:

Which, in time (T_{universe past present in non-g} = H_{universe past present in non-g}/c) is 4.3345010∙10¹⁷s. Since one tropical/solar year is 3.1556926∙10⁷ s [14], this equates to 13.7355010 billion years (≈ 13.7355 billion years) according to our present knowledge [15]. As a check, since 1 light year equals 9.4605284∙10¹⁵ m (x=c∙t_{1tropical year}), the radius of the cosmos in light-years is as follows:

Figure 1. Dualistic Earth (in terms of movement) The relationship between the entire plane angle (2∙π) and the deviation angle of a light beam (c) coming from the galaxy on the left grazing the Earth (α_Earth) is illustrated above. (The expanding universe is represented as a light gray circle and the Earth in the center as a black dot.) If the same beam passes through the gravitational field of the Earth (g = 9.8m∙s^-2) while the Earth is in motion (n·α_Earth) (Fig.1.a) or is comparatively static (α_Earth) (Fig.1.b), then the degrees of change in the properties of light (e.g. deflection) are different. In the left-hand figure, compared to the opposite galaxy (with a redshift of 3.14 for example) the Earth moves away from A to B with the same velocity, together with the light beam in its g, along their contact distance h_{past present in g}. This relative one-dimensional movement of the galaxy and the Earth in three dimensions forms a sphere with the radius of h_{past present in g} (the dark gray circle) around the planet. Because of the Earth's movement with various redshifts, this sphere also contains a homogeneous gravitational field with a value of 9.8 m∙s^-2. During the generation of the contact distance (h_{past present in g} = n∙R_Earth) there will exist a concentric relationship between the increasing radius of the universe and the size of the Earth. From this data (h_{past present}, 2∙π and α_Earth), based on Euclidean geometry, the size of the universe (H_{universe past present in non-g}) (right hand figure) in the case of the inverse ratio of angles (α/2∙π^-1) as well as the Earth's radius (R_Earth) can be determined symmetrically. (The striped circle in Fig.1.b occupies the same space as in Fig.1.a).

4. Calculation of the Size of the Earth

Similar to the above idea, looking for the validity of symmetry towards smaller units of concentric spheres in geometry, a mathematical approach with the following pair of ratios can be given. The ‘short evolving distance’ (h_{past present in g}) (Eq.3) can be provided by the ratio of the deviating angle (α_{Earth in g}) of a light beam passing near the Earth’s surface as a result of the gravitational field (g) and of the entire plane angle (2∙π) [12].

With this ratio, a previously unknown length can be calculated which falls in the range of the radius of the Earth (h_h(Earth)) [16]. 

The deviation angle (α_{Earth in g}) of a light beam, which passes near a celestial body’s surface according to Einstein’s formula, is α = 2×G×M×c^-2×R^-1. Therefore:

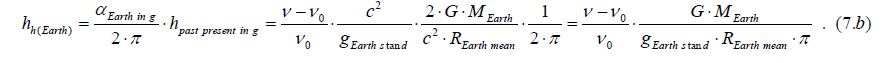
Where h_{h(Earth in g)} is the radius of the Earth, (ν-ν_o)/ν_o is the ratio of redshift of the Milky Way Galaxy (including the Earth). The c is the speed of light (2.99792458·10⁸ m·s^-1), G is the gravitational constant (6.673848·10^-11 m³·kg^-1·s^-2), M is the mass of the Earth (5.97219·10²⁴ kg), g is the standard gravity of the Earth (9.80665m·s^-2), π is 3.141592 and R is the volumetric mean radius of the Earth (6.371005·10⁶ m). (The parameter references are the same as in Equation 6.)

When this method is extended to such a large redshift of 3.141592, which can be measured at farther/farthest galaxies [17] substituting the values into the formula, the equatorial radius of the Earth can be calculated:

Taking into account the gravitational refractive index (n_g) [18], which can influence the average value of the Earth's radius in a positive and negative direction the values are as follows: 6179.9355 km (6379.42 km∙0.96873) and 6585.3043 km (6379.42 km∙1.0322732) [19]. This is a roughly plus-minus 200 km deviation from the average.

5. Relationship between the Radius of the Earth Running by Light and of the Age of the Cosmos: A "Dynamic Space-Time Curvature Aging"

Based on the properties and symmetry of concentric circles and spheres, this model is also suitable for calculating the age of the Earth, which is between 4.55 and 4.404 billion years according to radiometric dating [20]. This method of dating, which is related to geometrical properties and the space-time curve resulting from the extreme degree of motion of the Earth, can be briefly called "dynamic space-time curvature aging" (see also Figure 1) and can be summarized as follows.

The distance of the Earth's radius (h_h(Earth))  is run by light (c) during the following time interval (t_hh(Earth)), which is as follows: 

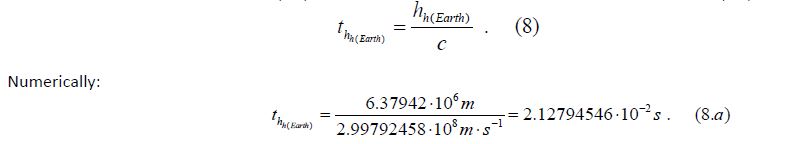
Starting from the short evolving distance (h_{past present in g}), moving upwards towards the larger distance values (H_{universe past present in non-g}) and going downwards the smaller radius (h_h(Earth)), the radii of the cosmos and the Earth can be determined symmetrically (Eq.6 and Eq.7). It is necessary to use the α/2∙π^-1 ratio to get from the smaller distance value to the one in the middle direction. Moreover, to reach the immense distance directly from the small one, the ratio should be used squared (α/2∙π^-1)². The same relationship applies to time intervals as to the fourth dimension of space-time, which can be transformed into each other according to general relativity. Therefore, if the time interval (t_hh(Earth)) in Equation 7 is multiplied by (2∙π/α^-1)², it could determine the age of the universe (T_{universe past present in non-g}):

(The same result can be obtained from formula 12.b.)

Numerically, this is:

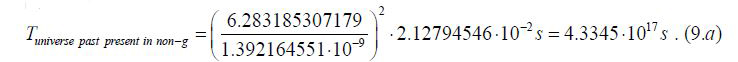
Since one tropical/solar year is 365.242189 days long or 3.1556926∙10⁷s, this value equates to 13.7355 billion years. It is equal to the result of the method for determining the age of the universe in Equation 6.

6. The Projection of the Age of the Universe for the Development of the Earth

Based on the previous geometry and the symmetry between the radius of the universe and of the Earth (Fig.1) [4], it is necessary to examine whether there is a correlation with respect to their age as well. If so, the extent of the quantitative discrepancy between them should also be clarified. In addition, to what extent do changes in the age of the universe affect the time of the Earth's origin.

6.1 The relationship between the age of the cosmos and the time of the formation of the Earth

The direct relationship between the age of the universe and the time of the formation of the Earth has not been known so far. However, the multiplier of three between them was known from experience. In the present work, given the above geometric representation through the symmetry observed in determining the distances (Eq.5 and Eq.7), an attempt can be made to find the relationships on the basis of which this multiplication factor of 3 could be explained.

6.1.a Determining the age of the cosmos

As is known, divided by the speed of light, the dimension of distance can be converted into a time dimension. In this way, by dividing both sides of the original formula (Eq.6), which defines the radius of the universe (H_{universe past present}) by the speed of light (c), the formula is modified as follows:

Since t_{h past present} is equal to 0.960395021∙10⁸ s (h_{past present}/c) according to Formula 3.a, the age of the cosmos (T_{universe past present}) is as follows:

Since one tropical/solar year is 365.242189 days long or 3.1556926∙10⁷s, this value (Eq.10.b) equates to 13.7355 billion years. It is equal to the result of the method for determining the radius and age of the universe in Equation 6.

6.1.b Determining the ‘Earth radius time’ from the ‘short evolving time’

Similar to the above, by dividing both sides of the formula (Eq.7.a) that determines the radius of the Earth (h_h(Earth)) by the speed of light (c), the equation is the following:

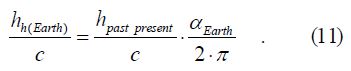
Then the distances in it (Earth radius /h_h(Earth)/ and ‘short evolving distance’ /h_{past present}/) can also be converted into time intervals (th_h(Earth), and th_{past present}):

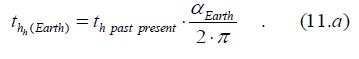
The time derived from the short evolving distance can be called ‘short evolving time’. Time resulting from the radius of the Earth can be defined as ‘Earth radius time’. Since the former (t_{h past present}) is 0.960395021∙10⁸ s, the exact time of the latter (t_hh(Earth)) is as follows:

6.1.c The relationship between the age of the cosmos and the ‘Earth radius time’

By arranging the age of the universe (T_{universe past present}) and the ‘Earth radius time’ (th_h(Earth)) for the value of the ‘short evolving time’ (t_{h past present}), the symmetry between formulas 10.a and 11.a can be clarified:

In this case, the connection between the age of the cosmos and the ‘Earth radius time’ is quite clear with regard to the elements that also carry symmetry.

Rearranging the unified equation (Eq.12.a) to the age of the universe (T_{universe past present}), the following relation appears:

Combining the individual components in the equation:

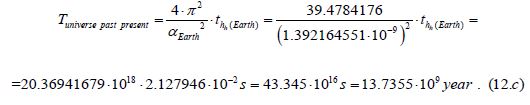
This reveals the numerical value of the proportionality factor or relational constant (≈2∙1019) between the two time intervals (T_{universe past present} and th_h(Earth)).

[Based on the above considerations (Eq.12), the relationship between the radius of the cosmos (H_{universe past present}) and the radius of the Earth (h_h(Earth):

The two distance values can be converted to each other by dividing or multiplying by the relational constant (4∙π²/α²).]

6.1.d Division of the relational constant between the two ages

If we want to match the time intervals in the combined equation, we can combine the proportionality factor between them and create a united expansion constant (k_{united(expansion)} = 2∙π/α or 2∙π∙α^-1). (Which can also be called the age determining correlation constant of the universe.) This constant gives a directionality to the dimensional component associated with it in the equation. This direction in this case, when the constant is located next to the radius of the Earth and increases it to an extreme degree, points from the present to the past. Since k is used twice in this case, its square /k_{united(expansion)}² = (2∙π/α)² = 4∙π²/α² or 4∙π²∙α^-2/ must be taken. The age of the cosmos (T_{universe present past}), derived from ‘Earth radius time’ (th_h(Earth)), is as follows:

If we divide the united expansion constant (k_{united(expansion)}) into 2 parts, we can distinguish in it a so-called geometric part of the united expansion constant (k_{geometric(expansion)} = 2∙π) and a part that can be called an expansion part of the united expansion constant (k_expansion =1/k_contraction = α_Earth^-1). The latter being an extremely large dimensionless number. The square of these is as follows: 4∙π² and α_Earth^-2.

The simplest way to denote this is a constant encoding a spherical spatial structure (k_{geometric(expansion)}² = 4∙π²) and representing a rapid expansion (k_expansion²=1/α_Earth²), which ultimately makes the two-time intervals equal:

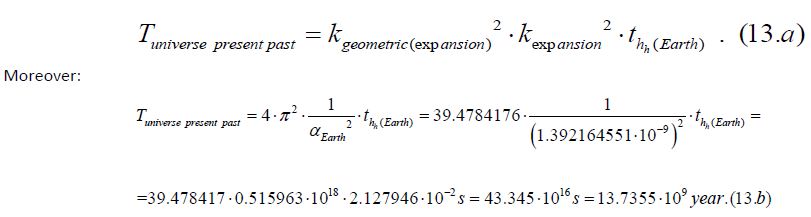
Looking at this from the opposite direction, that is, from age value of the universe (T_{universe past present}) to the ‘Earth radius time’ the formula is modified as follows. This constant also gives a directionality to the dimensional member associated with it (T_{universe past present}) in the rearranged equation (Eq.13).

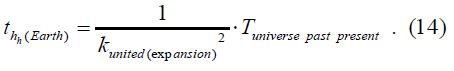
The inverse of the united expansion constant (1/k_{united(expansion)} = α/2∙π) can be called the united contraction constant (k_{united(contraction)} = α_Earth/2∙π^-1), which is a significantly minuscule dimensionless squared value (k_{united(contraction)}² = 1/4∙π^-2∙α_Earth²).

This direction, when the value of the constant reciprocal modifies the radius of the cosmos, i.e. reduces it to an extreme extent, points from the past to the present. If we divide the united contraction constant (k_{united(contraction)}) into 2 parts, we can distinguish in it a so-called geometric ​part of the united contraction constant (k_{geometric(contraction)} = 2∙π) and a part that can be called an contraction part of the united contraction constant (k_contraction =1/k_contraction = α_Earth):

Moreover:

Finally, the ‘Earth radius time’ (t_hh(Earth)), (which includes the both the ‘intrinsic’ geometric part of the united contraction constant and the ‘intrinsic’ contraction part of the united contraction constant of the cosmos’), is given numerically as follows:

As the right and left sides of the equations (Eq.13 and Eq.14) are reversed, the time conditions change. A 180-degree turn is made between the present and the past, while the k constant becomes itself reciprocal. It also means a motion from the present to the past, and a spatial motion up and down perpendicular to the time axis (increasingly widening/expanding space-time). This results in a time-dependent dynamic horizontal, and vertical change in the structure of space-time. The expansion and contraction of space, being of equal size, cannot annul each other separately, but considering both cases, they can (k_contraction∙k _expansion = 1 and α_Earth∙1/α_Earth = 1).

For ‘Earth diameter time’ (2∙t_hh(Earth)), which could be named ‘extrinsic’ part of the united contraction constant of the universe, the periods on both sides of the equation are as follows:

In the case of the ‘Earth perimeter time’ (2∙π∙t_hh(Earth)), which is also an ‘extrinsic’ part of the united contraction constant of the cosmos:

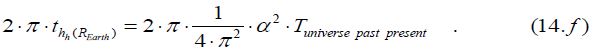
By dividing and multiplying by the speed of light as a universal constant, the time dimension can be converted into a distance dimension and vice versa. Therefore multiplying these time interval values (th_h(REarth), 2∙ th_h(REarth), 2∙π∙th_h(REarth)) by the speed of light (c) gives the radius, diameter and perimeter of the Earth (h_h(REarth), 2∙ h_h(REarth), 2∙π∙h_h(REarth)) respectively. Therefore, in contrast to Equation 6, in this case, the extreme degree of time difference in the equation (Equation 10) can be converted to a distance or spatial dimension, i.e., space expansion or space contraction can occur.

Applying this principle to the time dimension, together with the three space-dimension, the four-dimensional space-time can be produced. In this way, the symmetrically constructed universe image can be reduced to these elementary geometric shapes (concentric spheres).

{The united expansion constant (k_{united(expansion)}) in the traditional sense numerically increases the distance h_h(Earth) and thus produces h_{past present} (t_{h past present} = h_{past present}/c). In the present context, this can be thought of trigonometrically as the distance (h_h(Earth)) arranged side by side several times (n) in succession. The clamps of the plane triangles opposite to the angle add up and the distance thus connected becomes continuous, forming h_{past present}. In a direction perpendicular to this, an empty space, which can also be considered to be substantially continuous, is formed from the elementary parts of the clamps next to the angle. Given that the constant is in the square (k_{united(expansion)}²), the same phenomenon occurs again and the distance H_{universe past present} is created from h_{past present} /Figure 1 on the right and see the former article Figure 3 [4]. Although the increase in space can be observed in the radial direction from the Earth, only the space formed starting from h_{past present} (which almost coincides with the distance of the nearest stars) can correspond to the united expansion constant (k_{united expansion}).}

6.1.e The relationship between the intrinsic geometric part of the united expansion constant of the age of the universe and the evolutionary time of the Earth

If we consider the geometric part of the combined expansion constant of the universe (k_{geometric(expansion)}=2∙π) and divide both sides of the combined equation by π, we get the following reduced value:​

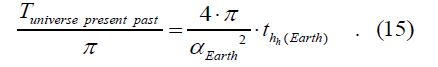
(Later, it can be state that not only π, but also 2∙π can be used to divide the age of the cosmos, or rather, the age increased by the time elapsed during its expansion, in which case we get the same value of the ‘Earth radius time’)

Numerically:

Since a tropical year is 365.242189 days or 3.1556926 ∙ 10⁷s, this value corresponds to 4.372144 billion years, which is equal to the average age of the Earth (T_{Earth past present}) in terms of symmetry resulting from distances (Eq.11).

Finally, the division of the unified equation (12.c) by π from the present to the past represents a large spatial jump backwards in time. Conversely, when checked, multiplying the reduced time value by π represents an equally large spatial leap from the past to the present. Continuing the line of reasoning and exiting from the unified equation (12.c), i.e. multiplying both sides of it by π, yields a large jump in space backwards, thus tripling the effective time. The increased cosmic size is due to the continued expansion of the cosmos over time. Alternatively, simply attributed to π, i.e. the corresponding number causing an increase, would also represent a spatial expansion in geometry. In this sense, multiplication and division by π can imply space expansion and the opposite, space reduction. In an ever-expanding cosmos, as time passes and light reaches our eyes during its 13.73 billion year journey (T_{universe past present visible by expansion}), the original radius increases in proportion (since x = c∙t, in this case H_{universe past present invisible by expansion} = c∙T_{universe past present visible by expansion}, i.e. 2.99792458∙10⁸m/s∙13.7355∙10⁹years∙3.1556926∙10⁷s = 12.9945∙10²⁵m). Assuming uniform expansion, the total distance is twice the original distance value (2∙12.9945∙10²⁵m ≈ 26∙10²⁵m), which is ultimately the actual size of the universe. In time (T_{universe past present visible by expansion} + T_{universe past present invisible by expansion}) that is 27.47093 billion years (T_{universe past present visible and invisible by expansion} = 2 ∙ H_{universe past present visible by expansion} ∙ c^-1 ∙ t_{tropical year}^-1 = 25.989017 ∙ 10²⁵m / 2.99792458∙ 10⁸ m/s / 3.1556926∙10⁷s). However, the value of time, i.e. the age of the cosmos, stops increasing and stops at 13.7355 billion years, for reasons explained later (see section 6.2.c and Eq.17.h).

6.1.f However, if we multiply both sides of the equation (Eq.13) by π, which shows the alternative appearance of π, the formula is modified as follows:

This equation is formally and numerically the same as in formula 12.c:

Since a tropical year is 365.242189 days, or 3.1555626 ∙ 10⁷s, this value corresponds to 13.7355 billion years (43.345·10¹⁶s/3.1557·10⁷s), which is equal to the average age of the cosmos (Eq. 6).

With this mathematical derivation, it can be seen that there is a direct relationship not only between the extent of the universe and the size of the Earth, but also between the age of the cosmos and the time of the Earth's evolution. Therefore, the time of the Earth's formation and the age of the universe are π times each other, and vice versa. In this context, one of the proportionality factors between the two is π. Consequently, if the expression 4∙π∙(α_Earth)^-2 is considered constant, the highlighting of π from the combined formula describing the relationships explains that the known proportionality factor between the age of the universe and the time of Earth's evolution is around 3.

If we consider all possibilities, which can be named ‘intrinsic’ geometric part of the expansion constant (k_{geometric(expansion)} = 2, π, 4, 2∙π, π², 4∙π, 2∙π² and 4∙π²) except k_expansion (1/α and its reciprocal, Eq.14), the following intervals can be placed on the timeline of the cosmos from its ‘center’ to its periphery. This is also necessary because if the equation defining the two distances leads to a correct result (Eq. 6 and Eq.7), then it is also obligatory to examine how each term in the equations influences the values determining the final result. These prominent members (k_{geometric(expansion)}) may contain information about certain details of the original idea. For Equation 12.c, if we divide both sides of the unified equation by k_{geometric(expansion)} = 2, 3.1415, 4, 6.2832, 9.8696, 12.5663, 19.7392 and 39.4784, the following time intervals of the universe are obtained. From the original cosmic age of 13.7355 billion years, these are as follows. 13.7355 Billion years/2 = 6.8677 billion years (developed galaxy of the cosmos, 13.7355 billion years/3.1415 = 4.3721 billion years back to the past (median age of the Earth), 13.7355 billion years/4 = 3.4338 billion years towards the past (evolving galaxies), 13.7355 billion years /6.28 = 2.1860 billion years towards the older past (evolving galaxies). Moreover, 13.7355 billion years/9.8696 = 1.3917 billion years towards the distant past, 13.7355 billion years/12.566 = 1.09306 billion years (end of reionization, early evolving galaxies of the cosmos). 13.7355 Billion years/19.74= 695.82 million years (primordial galaxies of the universe) [21], finally 13.7355 billion years/39.4784 = 347.92 million years (beginning of reionization, creation of the first stars of the cosmos) [22]. Since the formula describing the universe does not contain a value grater thane 4∙π², it is no longer possible to determine the period shorter than 348 million years defined by it towards the point of the origin of the cosmos.

In relation to Equation 12.c, for symmetrical reasons, multiplying both sides of the combined equation by 2, 3,1415, 4, 6,2832, 9,8696, 12,5663, 19,7392 and 39,4784, we obtain a true cosmic age in the first four cases, which are compatible with what has already been defined. In the last three cases, difficult-to-interpret data are available. Therefore, from the original cosmic age of 13.7355 billion years, these are as follows. 13.7355 billion years ∙ 2 = 27.46 billion years (twice the age of the cosmos, the age resulting from the diameter of the universe). Moreover, 13.7355 billion years. 3.1416 = 43.16 billion years (π times the age of the universe, half of the total age of cosmos, half of the visible and invisible parts of the universe). 13.7355 Billion years. 4 = 54.94 billion years (four times the age of the cosmos). Furthermore, 13.7355 billion years ∙ 6.2832 = 86.3 billion years (2∙π times the age of the universe, π times the diameter age of the universe, the total age of the cosmos).

Expressed in a geometric interpretation that takes into account the types of motion existing in the cosmos, this period is the one-time reversal time interval of the universe that can be observed relative to us. Moreover 13.7355 billion years ∙ 9.8696 = 135.56 billion years (π² times of the age of cosmos), 13.7355 billion years ∙ 19.74 = 271.14 billion years (π² times the double age of the universe), finally 13.7355 billion years ∙ 39.478 = 542.255 billion years (π squared of the fourfold age of the cosmos, the square of the perimeter age of the cosmos) (Eq.14.f). Expressed also in a geometric interpretation that takes into account the motions existing in the universe, this period is the six-time reversal time interval of the total age of cosmos (542.255 b.y./2/3.141592=86.3 billon years).

Figure 2. The geometric and expansion/contraction part of the cosmos. The former is shown on both sides of the figure, the latter in the middle, between the two vertical lines (not to scale). The middle horizontal line is the average age of the universe. The top two are a reduced and an increased time period version (the difference between the two is 4∙π²). The bottom two are a left and a right shifted average cosmos time interval option. In the former case, it means a displacement in the direction of the radius of the universe or in the direction of its circumference. In the latter case, it means an increase in the size of the Earth, or a shift in the perimeter of the planet.

All of these can also represent a stretched and compressed version of space-time according to the given situation. Each extreme also indicates the limit within which the cosmos can persist at all, in time interval or volume. Not only in the case of the shortened or elongated universe age, but also in the case of the shifted time intervals are tensions within themselves relative to each end. In the case of a cosmic radius wrapped in a perimeter, the average size and age of the universe remain unchanged. The difference due to geometric reasons is lost through different mechanisms and phenomena (Figure 3). The excess radius observed in the cosmos is digested in the direction of distant stars, in the case of the Earth it disappears in plate tectonics or in the mechanism of continental migration. The lack of radius in the early universe may indicate the division of the layers of the inner boundary. In the case of the Earth, it can participate in the formation of its internal structure or be traced in its division.

6.2 The geometric basis of the similarity between the size and shape of the cosmos and the Earth

6.2.a The total size of the universe expressed in the radial direction

However, for symmetrical reasons, it is necessary to examine what happens if we do not divide Equation 12.c, but multiply it by π. In this case, we exit the combined Einstein formula for determining the radius and age of the universe. Even if we multiply by π the maximum value determined by the formula, which in this sense can be considered as a boundary surface (in 3D as a volume), crossing the limit of the equation we get to an unknown area, which can be named H_{universe past present beyond the horizon1}. This is:

Then the radius of the cosmos will be π times the known visible part of the universe, i.e. 13.7355 billion light years:

If this radius (Eq.15.a), which partly includes the visible range of the cosmos up to 13.7355 billion light-years and partly the areas beyond this region, is multiplied by 2, the next distance can be obtained in light-years. This corresponds to the greatest distance in the universe:

This distance, which can be called H_{universe past present beyond the horizon2 (total),} also corresponds to the diameter of the cosmos:

If the age of the universe (T_{universe past present} = 13.7355 billion years) increases with gravitational refractive index (n² = 1.06558) [18]. and reaches 14.6363 billion years, the size of the universe (multiplied by π) named as H_{universe past present beyond the horizon1.corr.by n}², will increase to nearly 46 billion light years:

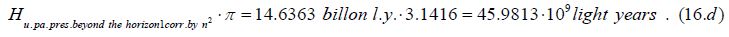
However, if we multiply this by 2, the dimension (diameter) of the cosmos reaches a distance of almost 92 billion light-years named H_{universe past present beyond the horizon2 (total) corrected by n}²:

/ Another correlation is that by multiplying the original age of the universe in light years (corrected by the gravitational refractive index, n² = 1.06558) by 2∙π, we obtain a distance of 91.9626 billion light years (14.6363 billion light years · 6.283185), i.e. the total size (the perimeter) of the cosmos. /

6.2. b The total size of the universe in curved form: the perimeter of the cosmos

Since values above 13.7355 (or 14.6363) billion years no longer increase the age of the universe, it is advisable to interpret them in terms of distances measured in light years. As explained above, these increased distance values may also indicate areas outside the visible range of the cosmos. These dimensions may be radial; they can represent the diameter of the universe (d), or perhaps even determine its perimeter (P). In the latter case, if we assume a curvature of space-time in the farthest areas of the cosmos, we can obtain information about the areas behind, similar to the curvature of light passing by massive celestial bodies. Then, due to the curvature of the light, the radially perceived areas are not located where they actually are. In this case, we can see the completely curved perimeter of the universe as a straight line (apparent line), that is, in a line thought in the radial direction (actual line).

In the case of multiplication by π or 2∙π, based on geometrical considerations (P =d∙π or P= 2∙r∙π), the increase in distance is not necessarily radial in connection with the curvature of the space-time structure. It is as if the increased radius corresponds to the circumference (P). In the case of a circle describing the complete geometric shape, similarly to the energy/material flow around the perimeter of the universe (2∙π).

 The perimeter of the universe (P_{universe past present}) in light years is as follows:

According to Eq.15.e, the corrected (by n²) circumference of the cosmos [18] is as follows:

6.2.c The perimeter of the Earth is derived from the circumference of the universe

Due to common mathematical roots, a phenomenon similar to the case of the universe can occur in the case of the Earth, when we also determine not the radius of the Earth (h_h(Earth)), but its perimeter (P_h(Earth)). This can be illustrated by the following mathematical equality, where the extent of the cosmos is on the left side of the equation and the size of the Earth is on the right side. Equality between the two parties may indicate symmetry in addition to arithmetic properties. Then both sides of the equation are multiplied by 2∙π.

Finally, the cosmos perimeter on the left side of the equation, after performing the mathematical operations, is equal to the equatorial perimeter of the Earth on the right side of the equation. The radius of the universe, which is thus greatly reduced by the appropriate factors (k_geometric²=4∙π² and k_expansion²=1/α_Earth²), can be described as a negative expansion i.e. contraction of space (k_contraction = 1/k_expansion = α_Earth, or k_contraction² = 1/k_expansion² = α_Earth²). This eventually decreases to the size of the Earth through a reduction in space, which can be seen as an extreme degree of shrinkage of the cosmos [23]. This may be an analogy to their appearance, through changes in the structure of space-time, it may represent a causal relationship in terms of their physical formation or functional changes.

With regard to the time dimension, it can be stated that the time interval (T_{universe past present total}) corresponding to the total size of the universe (H_{universe past present total}) is required at the time of age determination. Although this distance, expressed in light years (H_{universe past present total in light years}), is much greater than that which results from the radius of the cosmos (H_{universe past present total in light years}). This value consists of two parts, one is the visible universe (H_{universe past present total}) and the other is the outside of this globular space (H_{universe total (diameter)}). This increased value is needed in determining the age of the Earth (T_{Earth radius}) because the question arises as to why we should only divide the age of the universe by π, when it could be 2∙π. However, in the latter case, we get a low value, i.e. half of the 4.372 billion years (2.186 billion years). The solution is to divide the number of billion years expressing the largest size (age) of the cosmos (H_{universe total (diameter) in light years}) by 2∙π, during which the time required for the Earth to form leads to the actual result (T_{Earth radius}).

Conversely, when we multiply the age of the Earth by 2∙π, we get the size of the entire universe (visible and invisible part) in light years (H_{universe total (diameter) in light years}). This mathematical approach arising from symmetry, due to the departure from the original formula (Eq.12.c) is like looking at the cosmos physically from the outside. This is because the multiplication by 2∙π is not originally included in the definition of the time-dimension (one more multiplication by 2∙π). Later, however, when dividing by π on both sides of the equation, we can look at the entire system from the inside. We then simply divide the radius (age) of the cosmos by π to determine the age of the Earth's formation and vice versa. Multiplying the radius of the cosmos by 2∙π increases the distance (age) in this proportion.

However, for geometric reasons, it can be assumed that the distance increase does not occur linearly but passes into the perimeter (P_universe=2∙π∙H_{(R) universe}). Physically, this can presumably mean that the increase in distance curves and surrounds the universe, forming its circumference (Fig.3.a). With respect to the time dimension, this phenomenon may appear that as the radial distance is curved, the time does not increase further, i.e. stops (in contrast to the perimeter, does not reverse) (Fig.3.b). 

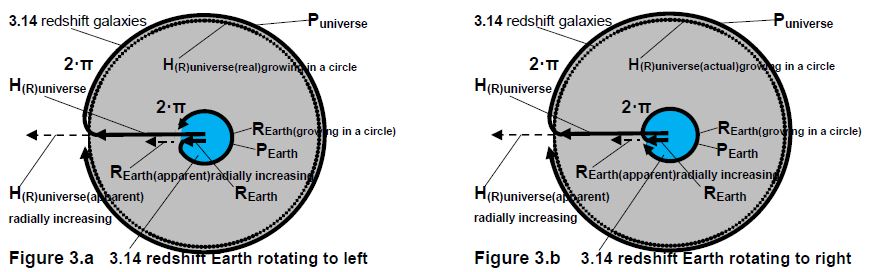
Figures 3.a and 3.b. The shape and structure of the universe and the Earth based on a consideration arising from geometric uniformity. The figures show the structure of the space-time surrounding the universe and the relationship between the cosmos and the Earth. The representation of the motion of the two of them can inform us to interpret the relationships with arithmetic derivations. Outlining relative forms of motion in a system can explain the geometric and arithmetic background of processes occurring in nature.

Figures 3.c and 3.d. The relationship between specific distance values or individual time intervals and the components of a circle or even a sphere can be highlighted. The directions of rotation can also change in connection with the direction of time, i.e. its progress towards the present or the past, which also affects the numerical data with the opposite sign.

This phenomenon can occur in all directions and presumably creates a dark, circular flow of energy-material of the primordial universe in connection with temperature changes (Fig.3.e).

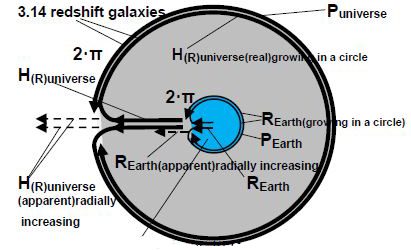
Figure 3.e In this figure, it can be observed that the Earth and the cosmos with a redshift of 3.14 can move in opposite directions in either direction, or even rotate parallel to each other. These alternative motions may correspond to different values obtained for the size of the universe or the radius of the Earth. These movements can add up or just subtract from each other (subsections 6.1.f and 6.2.d).

In this way, the values obtained can be variations of these complex movements and satisfy the possibilities inherent in the equation (Eq.12.a). The compensating motion can eliminate the perimeters, leaving only the original cosmos radius and the rotations relative to each other in the case of the Earth and cosmos. In the case of the maximum redshift (3.14) in the opposite direction, interpreted in one dimension (but also extended to the three dimensions) (Figure 1.a), a certain driving force may occur due to the changes caused by the structural differences of space-time. Which can then affect the functioning of the components (cosmos and Earth) of the entire system.

This phenomenon can occur based on the following causal relationship. The combined Einsteinian formula (Eq.6.) shows that there is an inverse proportionality between the strength of gravity and the size of space. Gravity increases as the volume of space decreases and decreases as the volume of space increases when the values of the other factors in the formula do not change. By reducing the size of the cosmos (H_{universe past present}) to the size of the ‘short evolving distance’ (h_{past present}) as in Figure 4.a, the total gravity due to this reduction in size (g_{universe at h past present}) could be calculated [24], and its value is:

For symmetrical reasons, a similar process can take place in the case of the Earth (Figure 3). The increase of the Earth's radius (h_h(Earth)) stops at a redshift of 3.14, and then the increase of the distance can continue, but it can no longer radially, but can bend to the growth of the Earth's perimeter (P_Earth). At 2∙π, the circumference of the Earth with its radius gives the entire circle (P_Earth=2∙π∙h_h(R)Earth). This mathematical approach can physically manifest itself in the form of convective heat and material flow from the inside of the Earth towards the surface. This radial process of magma current in the mantle of the Earth can result in lateral drift of the Earth’s crust plates. In this way, the conditions for the drift of the crustal plates and thus for the migration of the continents are created. In this context, the process of subduction of tectonic plates is also ensured [25]. This phenomenon due to changes in the space-time structure may therefore be the origin of these movements in connection with changes in temperature.

{In addition to geometrical considerations, an additional supporting option can be formulated in relation to the contraction of space. From the original Einstein equation determining the ‘short evolving distance’ h_{past present} of the universe, we can express the value of the gravity going back in time. Going towards the formation of the universe, with the conical decrease of the cosmos volume, in parallel, the strength of the gravitational field increases to an extreme extent. The constraining effect of the immense space curvature formed during the decrease from h_{past present} to h_h(Earth) may already justify that the radius of the Earth does not increase in the radial direction, but turns in the direction of the circumference. Going back in time and reducing the radius of the cosmos from the size of the ‘short evolving distance’ (h_{past present}) to the radius of the Earth (h_h(Earth)) the gravity could be calculated (g_{universe at Earth’s radius}) on the bases of the original Einsteinian Equation 3:

The combined Einstein’s formula (Eq.17.f) also shows that there is an inverse proportionality between the strength of gravity and the size of space. Gravity increases as space decreases, and decreases as space increases. This contraction of the space-time structure of the universe results in a black hole phenomenon that can occur in parallel with the formation of the Earth (Eq.4.b). However, at the size of H_{universe past present} the value of the surface gravity of the Earth (g_{Earth standard}) can be maintained as in Eq.3. Further on, this space-time contraction reaches the limit of 3.14 according to the redshift in the formula. As in the case of the expansion of the universe, similar dynamics are created in this case, only in the opposite direction. As a mirror image of the expansion of the cosmos, a redshift accelerating to almost the speed of light is formed according to the transformation shown in Fig. 1. Here, the space does not expand but, on the contrary, narrows. Moderating velocity, like gradually increasing time dilatation (Eq.17.h), can only create the conditions for the processes that take place in and around the black hole to be tamed into Earth conditions:

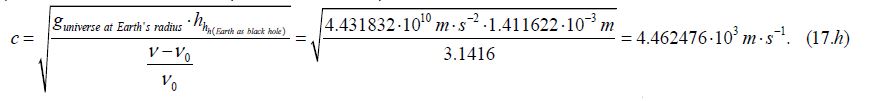
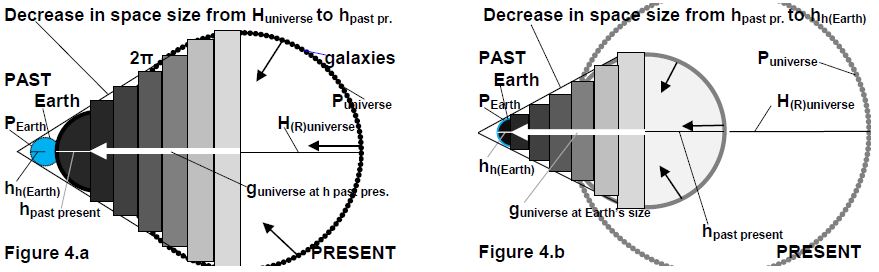
Figures 4.a and 4.b. The decrease of the two space parts (volumes) of the universe (black arrows) and the parallel increase of the gravitational field strength (g) are shown in the figures (white arrows). These extend back in time, from the size of H_{universe past present} to the size of the ‘short evolving distance’, h_{past present} (Fig.4.a) and from h_{past present} to the radius of the Earth (h_h(Earth)) (Fig.4.b) from the present to the past (not to scale).

6.2.d The division of the inner layers of the Earth is derived from a phenomenon similar to the mechanism of the decreasing size and age of the universe

To clarify the role of the factors (k_united = k_{geometric(expansion)}∙k_expansion; Eq.13.a) in the equation for determining the radius of the cosmos and the Earth, we can examine whether there is this relationship between the following quantities and reality. Based on the mathematical solutions below and these results, the following conclusions can be made, which are approximately the same as our already known geological knowledge regarding the structure of the Earth [26].

Similarly, as in 6.1.d, by dividing both sides of the combined equation (eq.12.c) by 2∙π, we can arrange the equation for T_{universe past present}/2∙π:

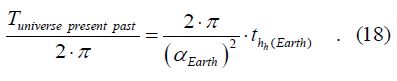
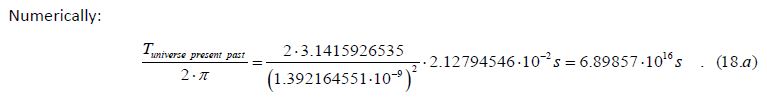
Since one tropical/solar year is 365.242189 days long or 3.1556926∙10⁷s, this value equates to 2.186 billion years, which is equal to the half of the average ‘Earth radius time’ (T_{Earth radius}).

This time interval (Eq.18.a), expressed in terms of meters, is as follows:

Dividing this distance (x) by the square of 2∙π/α, we get the radius of the Earth, which in this case will be smaller than average. This radius (1015.31 km) is approximately equal to the size of the Earth's inner core (h_{h (Earth)inner core}):

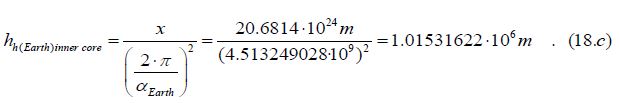
{A further approximation can be achieved by multiplying by the square of the refractive index (n_g²) of the universe (at which time the size of the inner core almost reaches the actual one /1.01531∙10⁶m ∙1.06558 = 1081.89 km/)}.

Multiplying this value by π, the radius is approximately equal to the boundary (3189.7 km) between the Earth's outer core and its mantle (h_{h(Earth) outer core-mantle}):

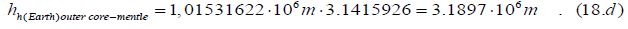
{Even more clarification can be obtained in the case of multiplication by the square of the refractive index of the universe (n_g²), in which case the size of the outer core approaches the actual one (3189.7 km ∙ 1.0655 = 3 398.88 km)}.

Finally, multiply this value by 2 to get the radius of the Earth's equator (h_h(Earth)), as in Eq.7.c:

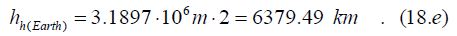
Further clarification can be obtained in determining the radius of the Earth by multiplying by the square of the refractive index of the universe (n_g²), in which case the radius exceeds the actual one (6379.49 km ∙ 1.06558 = 6 797.8569 km), but the excess length (106.558%, 418.367 km) is lost in plate tectonics by bending the radius into the perimeter.

As we did in defining the perimeter of the universe and looking along the radius from the present to the past, which turned toward the perimeter due to the curved space, this phenomenon may be true for the Earth for symmetrical reasons. Further, the opposite may be true, so considering the change of direction, if we look from the direction of the present, i.e. from the Earth's perimeter to the spherical origin corresponding to the past, then the perimeter can turn in the direction of the radius and point to the center of the Earth.

However, in conjunction with formula 12.c, extending the above line of reasoning and if we examine all possibilities of k_{geometric(expansion)} (2, π, 4, 2∙π, π², 4∙π, 2∙π² or 4∙π²). Except for 1/α = k_expansion and α= k_contraction, and use the distance values defined by them, the following intervals can be surveyed for the radius of the Earth, from its center to its surface. In the case of formula 12.c, dividing both sides of the equation by the members (2, 3.1416, 4, 6.2832, 9.8696, 12.5663, 19.7392 and 39.4784) gives smaller Earth radii. These values may correspond to the structural division of the Earth. Although there is not necessarily a clear causal relationship between the distance values determined by these variations and the already known geological structure of the Earth, they can be drawn in parallel. It can then be observed that these sections overlap approximately and are not substantially different in order of magnitude. These are the following, 6379.49 km/2 = 3 189.745 km (≈ core and mantle boundary of the Earth), 6379.49 km/3.14159 = 2 030.656 km (≈ outer core of the Earth), 6379.49km/4 = 1 594.87 km, 6379.49 km/6.2832 = 1 015.33 km (≈ inner core of the Earth). Moreover, 6379.49 km/9.8696 = 646.37 km (≈ asthenosphere of the Earth), 6379.49/12.566 = 507.66 km, 6379.49/19.74 = 323.17 km and 6379.49 km/39.4784 = 161.58 km (≈ crust and lithosphere of the Earth) [27].

6.2.e Plate tectonics; the migration of the continents of the Earth derived from a mechanism similar to the increase in the size of the cosmos

In the case of Equation 12.c, after a huge reduction in space in proportion to the angles, by multiplying both sides of the equation by the components in the equation (2, π, 4, 2∙π, π², 4∙π, 2∙π² or 4∙π² and α/2∙π^-1), we obtain oversized Earth radii. In conjunction with formula 12.c, extending the above line of reasoning and if we examine all possibilities (2, 3.1415, 4, 6.2832, 9.8696, 12.5663, 19.7392 and 39.4784) and use the distance values defined by them, the following intervals can be surveyed for the perimeter of the Earth.

Although, so far there is not necessarily a clear causal relationship between the distance values determined by these variations and the already known geological crust tectonic movement of the Earth, they can be adjusted in parallel. However, these increasing distance values may therefore correspond as a causal relationship to the process resulting in the continental drift of the Earth. According to them, an increase in the Earth’s perimeter caused by an increase in distance would force continents to migrate. This phenomenon may not be caused by the increase in the spatial extent of the Earth, but by the partial or even multiple reversal of the perimeter. This is because, as the continents migrate, there is a continuous subduction of oceanic plates. According to them, the immersion and dissolution of oceanic plates would digest the increase in circumference. Thus, the perimeter excess would not increase the growth of the Earth in the radial direction, but would be imperceptibly annihilated in the deeper, warmer layers of the Earth's asthenosphere in a circular direction. These distances are the following, 6379.49 km∙2 = 12 758.98 km (the diameter of the Earth), 6379.49 km ∙ 3.1415 = 20 041.74 km (half of the equatorial perimeter of the Earth), 6379.49 km∙4 = 25 517.96 km, 6379.49 km∙6.2832 = 40 083.48 km (the equatorial perimeter of the Earth). Moreover, 6379.49 km∙9.8696 = 62 963.014 km, 6379.49∙12.56 = 80 166.96 km (twice the equatorial circumference of the Earth), 6379.49∙19.7392 = 125 925.87 km (π times the equatorial circumference of the Earth), 6379.49 km∙39.4784 = 251 851.74 km (2∙π times the equatorial circumference of the Earth).

The sum of the Earth's circumference (P=2∙π∙h_h(R)Earth) and radius (h_h(R)Earth) is modified as follows, taking into account the square of the gravitational index of the universe (n_g²):

The process of turning the perimeter of the Earth into its radius, or vice versa, can be compared to describing a shape similar to the capital G. However, due to the deficit of the total sum of the perimeter and radius, the angular nature is lost and becomes rounded in both directions. The difference between the two distance values, expressed as a percentage, will be about 92% (42712.652 km/46 463.437 km =0.91927) as in the Figure 3.

6.3 The modifying effect of the gravitational refractive index of the universe on the evolution time of the Earth and Solar System

In the previous article, it was shown that even a special coefficient can be assumed between a long evolving distance (H_{universe past present}) geometrically derived from a short evolving distance (h_{past present}) [18]. The difference in the propagation velocity of light traveling in gravity (c₀), or non-gravitational space (c), results in a change in the radius of the universe. This gravitational refractive index of the universe (n_g) that modifies the average age of the cosmos also applies to the age of the Earth (T_{Earth past present}), which to our current knowledge is approximately 4.5 billion years [28] In the case of values that correct the average age of the cosmos downwards, these may refer to the previous developmental states of the Earth [29], while the values that increase the age of the universe may be related to the age of the Sun or the entire Solar System [30].

Upward correction of the age of the universe is possible by increasing the value of n_g, which can be a maximum of 1.1354777 (1.0322732⁴), then the formula is as follows:

Since a tropical year is 3.1556926∙ 10⁷ s, the elevated age of the cosmos corresponds to 15.596348 billion years [31], which, divided by π, is the age of the Earth’s more distant environment (T_{Earth past present}: 4.964472 billion years). (The time difference between the actual age of the Solar System and this time is likely to disappear due to the time dilation that causes distance contraction.)

The downward correction of the age of the cosmos is possible by gradually decreasing the value of n_g, which can be a minimum of 0.8806866 (0.96873⁴), then the formula is the following:

Since a tropical year is 3.1556926 ∙ 10⁷ s, the downward corrected age of the cosmos corresponds to 12.09666 billion years [32], which, divided by π, is the earlier stage of development age of the Earth (T_{Earth past present}: 3.85049 billion years).

However, these values may change based on the relationship with gradually increasing gravitational refractive indices (n_g) associated with the four-dimensional space-time structure [18]. These can alternate between two extreme values of the age of cosmos deviating from the mean in positive and negative directions (minimum: 12.1 and maximum: 15.6 billion years) (Chaboyer 1996): n_g = 0.96873 and n_g = 1.03227; n_g = 0.93845 and n_g = 1.06558; n_g = 0.909109 and n_g = 1.099978; moreover n_g = 0.88068 and n_g = 1.1354. This could also be paralleled with the developmental stages of the Earth: 4.235427 (4.372144 billion years · 0.96873) and 4.51323 billion years (4.372144 billion years ·1.03227); 4.10303 and 4.65887 billion years; 3.974755 and 4.809262 billion years; finally, 3.850487 and 4.964457 billion years respectively.

6.3.a The effect of the age of the universe determined by changes in the CMBR on the time of development of the Earth

Using the properties and symmetry of concentric circles and spheres, this model is also suitable for differently defining the age of the Earth, which is 4.55 billion years [34]. This method consists of determining the cosmos age associated with changes in Cosmic Microwave Background Radiation (CMBR) [15, 35] and the Earth's evolution times that can be calculated from it. In this way, dividing the average age of the universe (13.7355 billion years) by π, as in Eq.6, the time interval is approximately equal to the age of the oldest rocks of the Earth, which is 4.3721 billion years [36]. In the case of the upper age limit of the cosmos (13.82 billion years) [15, 37] this era is 4.4 billion years, which is closer to the interval of Earth's development time. Taking account of the lower age limit of the cosmos (13.688 billion years) [15, 38] this era is 4.357 billion years.

7. Derivation of the Time of the Formation of the Solar System From the Age of the Cosmos

Based on the above geometry (Figure 1) and the symmetry between the size of the universe and the radius of the Earth (Eq.6 and Eq.7), we can also examine the extent to which the age of the universe can correspond to the time of formation of the Earth’s wider environment. Positive and negative differences in the age of the universe (Eq.15 and Eq.15.a), like those in the time of the Earth's origin, may indicate the time of the formation of the Solar System (T_{Solar System past present}). In this case, however, larger deviations need to be taken into account. In this widened range, we can find the time intervals required for the formation of the entire Solar System.

Based on the formation of the Sun and planets, including the oldest comets and asteroids, the total age of the Sun may be 4.49±0.04 billion years, while that of the entire Solar System will be slightly more 4.568 billion years [39]. In our model, using the refractive index (n_g,min) introduced to correct the radius of the cosmos, the square of this value must also be utilized (n_g:1,03227²). As it appears, a total of 2 times, it appears one time to h_{past present} and one time to H_{universe past present in non-g} (1.03227∙1.03227). Therefore, this value is the most appropriate to determine the age of the entire Solar System. Ergo, dividing the cosmic age of 14.6363 billion years (13.7355 ·1.06558) by π, we get a time interval (T_{Solar System past present}: 4.659 billon years) of about 90 million years longer than the previous one. This is also slightly longer than that of the Sun (4.56-4.6 billion years) or Pluto (4.46-4.6 billion years) or the oldest comets and asteroids (4.6 billion years) [40].

8. Discussion

Using the ratio of the complete angle and the deviating angle of a light beam passing through the gravitational field of the Earth symmetrically (α/2∙π^-1 and 2∙π/α) could determine the age of the universe and the radius of the Earth as well. The multiplication and division by π, 2∙π or 2∙π/α refers to the correlations between the common mathematical (geometrical) and physical bases of phenomena. In addition, this method of determining the distance is comparable to the methods of determining the length based on the gravitational lens effect, and may form a special case of it. By placing the Earth in the model of the expanding universe, we can take advantage of the possibility that the Earth could exert an extreme gravitational effect on light by multiplying its mass, thus creating a large gravitational lens effect similar to galactic clusters.

9. Conclusion

Both in the context of the high redshift Milky Way galaxy (including Earth) in relation to the expanding universe and in terms of the quasi-static Earth, the cosmos can be described in several ways. This model, from a different perspective than before, seems to be able to approach the very accurate astronomical measurement results that can be achieved at the highly advanced technical level of the age. The association of algebraic calculations with geometric shapes, in the context of changes in space-time, may lead to some similarities in the structure and function of the Earth and the universe. The correspondence between natural laws and mathematical descriptions may be valid in this approach as well, and may contribute to the description and interpretation of difficult-to-access phenomena.

10. Acknowledgments

I would like to thank the physicist Zsolt Dankó for reviewing the article (University of Debrecen, Kenézy Campus, Department of Radiology).

References

1. Hubble, E.P (1929) A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae. Astronomy 15: 168-173.
2. Lemaitre, G (1931) The Beginning of the World from the Point of View of Quantum Theory. Nature 127: 706.
3. Lemaître, G (1933) l’Universe an expansion. Annales de la Société Scientifique de Bruxelles A53: 51-85.
4. Nagy, E.T (2015) The age of the universe the size of the Sun and planets based upon the Theory of General Relativity and Euclidean geometry. v1.0.
5. Einstein, A (1920) Relativity the special and general theory. H. Holt and Company, New York.
6. Young, P., Gunn, J. E., Kristian, J., Oke, J. B., & Westphal, J. A (1980) The double quasar Q0957 + 561 A, B – A gravitational lens image formed by a galaxy at Z = 0.39. ApJ, Part 1 241: 507-520.
7. Einstein, A (1911) On the Influence of Gravitation on the Propagation of Light. Ann Phys 35: 898-908.
8. Hubble, E.P (1926) Extragalactic nebulae. ApJ 64: 321-369.
9. Beckwith, S.V.W., Stiavelli, M., Koekemoer, A. M., Caldwell J. A. R., Ferguson H.C. (2006) The Hubble Ultra Deep Field. AJ, 132: 1729-1755.
10. Committee on Data for Science and Technology (2010) (CODATA). Recommended Values of the Fundamental Physical Constants.
11. NASA (2021) Science Solar System Exploration, Earth.
12. Herrmann, J. (1990) dtv-Atlas Astronomie. Deutscher Taschenbuch Verlag GmbH & Co.,
13. München. Bacon, R., Conseil, S., Mary, D., Brinchmann, J., Shepherd, M (2017) The MUSE Hubble Ultra Deep Field Survey. A&A, 608 A1.
14. Convert Units (2021) Measurement Unit Converter. Convert tropical year to seconds.
15. Bennett, C.L., Larson, D., Weiland, J. L., Jarosik N., Hinshaw, G (2013) Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps And Results. AJ Supplement Series 208: 20-54.
16. Clynch, J.R (2002) Radius of the Earth - Radii Used in Geodesy. Calhoun: NPS Institutional Archive 23
17. Bouwens R.J., Illingworth G.D., Oesch P.A., Stiavelli M., Dokkum, van P (2010) Discovery of Z ∼ 8 Galaxies in The Hubble Ultra Deep Field from Ultra-Deep Wfc3/Ir Observations. ApJ, 709: L133–L137.
18. Nagy, E.T. (2020) Earth in the Expanding Universe: A Dualistic Approach to Determine Their Physical Parameters based on a Combined Einstein Gravity Field Equation Using the Hubble Law.
19. Carroll, J., Hughes, S.W (2013) Using a video camera to measure the radius of the Earth. Physics Education, IOP Publishing Ltd 48: 731.
20. Wilde, S. A., Valley, J. W., Peck, W. H. & Graham C.M (2001) Evidence from detrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyr ago. Nature, 409: 175-178.
21. ESO (2016) ALMA Observes Most Distant Oxygen Ever.
22. Space.com Staff (2011) First Galaxies Born Sooner After Big Bang Than Thought.
23. Hogan, M (2019) The Universe is Expanding, But It’s Also Shrinking.
24. Nagy, E.T (2016) Determining the size, mass, gravity and density of the present and primordial universe by means of a modified Einstein’s gravitational field equation.
25. Meinhold, G. & Celal Sengor, A. M (2019) A historical account of how continental drift and plate tectonics provided the framework for our current understanding of paleogeography. Geological Magazine 156: 182-207.
26. Kissling, E (2015) Plate Tectonics, The tectonics of lithospheric plates. ETH Zürich-Geophysics.
27. Montagner, J.P (2011) Earth’s Structure, Global. In book: Encyclopedia of Solid Earth Geophysics 144-154.
28. Hazen, R.M (2010) How Old is Earth, and How Do We Know? Evolution: Education and Outreach 3: 198-205.
29. Dickin, A.P (2005) Radiogenic Isotope Geology. Cambridge University Press, ISBN 0 521 53017 2: 492.
30. Connelly, J., Amelin, Y., Bizzarro, M (2008) Chronology of the Solar System's Oldest Solids. ApJ 675: L121-L124.
31. Jimenez, R (1998) Globular cluster ages. PNAS, 95: 13-17.
32. Krauss, L.M., Chaboyer, B (2003) Age Estimates of Globular Clusters in the Milky Way: Constraints on Cosmology. Science, 299: 65-69.
33. Chaboyer, B (1996) The Age of the Universe. Nuclear Physics B, Proc.Suppl 51: 10-19.
34. Braterman, P.S (2013) "How Science Figured Out the Age of Earth". Scientific American.
35. Nagy, E.T (2016) The Effect of Surface Gravity, Tilt, and Motion of the Earth on the Age of the Universe based upon the Theory of General Relativity and Euclidean Geometry. v1.0.
36. Oskin, B (2014) Confirmed: Oldest Fragment of Early Earth is 4.4 Billion Years Old. Live Science.
37. Nagy, E.T (2021) “Study on the Effect of Variations in Earth-Surface Gravity Depending on the Shape and Position of the Earth Radius and Age of the Universe Using General Relativity and Euclidean Geometry”. Challenging Issues on Environment and Earth Science 8: 89-103.
38. Ade, P. A. R., Aghanim, N., Arnaud, M., Ashdown, M, Aumont, J (2016) Planck 2015 results XIII. Cosmological Parameters. A&A 594: 13.
39. Bouvier, A., Wadhwa M (2010) The age of the Solar System redefined by the oldest Pb-Pb age of a meteoritic inclusion. Nature Geoscience 3: 637–641.
40. Faulkner, D (1997) Comets and the age of the solar system. Journal of Creation, 11: 264-273.