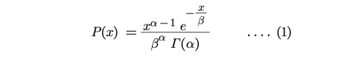Albert Einstein and Hermann Minkowski forged the concept of spacetime (1,2). In Einstein’s General Theory of Relativity (GTR) spacetime is flat until the introduction of mass into the region. The greater the mass the greater the curvature of spacetime. This adynamic model of spacetime has been successful in explaining significant observations such as the deflection of light by the sun. However, GTR does not provide a mechanism for the three other fundamental interactions. It is possible that a model of space in which changes in curvature and other geometric properties in the absence of mass or energy are chaotic, can provide the foundation for the unification of these four interactions.
Gravity as an Organizing of Space
In this model the shape and movement of space changes chaotically in the absence of mass or energy. Inside a mass this movement and geometry is less chaotic and conversely more organized. Space inside mass is integrally connected and influences space outside of the mass. With fewer constraints on movement and shape change the organization of space outside of a mass decreases as a gradient as the distance from the mass increases. In this way gravity is a function of the organization of space. The greater the mass the greater the organization of space. If this is the case, then two masses in proximity to each other would establish a region of ordered space between them that would be less chaotic than the space around their surfaces that face away from the region between them. The difference in organization between the turbulently changing space around the opposite surfaces of the masses relative to the organization of the space between them is the driving force of gravity [1].
The Strong Interaction as an Extension of Gravity
The strong interaction is responsible for the attraction between nuclear protons and neutrons. It must be strong enough to overcome the large electrostatic repulsion of positively charged protons that are very close together inside the nucleus. The strong interaction is significant only in the femtometer range of distance. If we calculate the magnitude of the gravitational interaction between two adjacent protons it is far less than the observed strong attraction as shown below,
Gravity is expressed as Newton’s law below,
F= G M1M2
r2
F = gravitational interaction, G is the gravitational constant. M1 and M2 are two masses, r is the distance between the center of each of the two masses.
The mass of a proton is 1.67 x 10-27 kg. The radius of a proton is 0.85 x 10-15meters. Therefore, if the two protons were adjacent to each other the distance between their centers, r, would be 1.7 x 10-15meters. The gravitational constant is 6.74 x 10-11 m3 kg-1 s-1
Given these values and using Newton’s law to calculate the gravitational attraction between two protons the following is obtained:
F= (6.74 x 10-11 m3 kg-1 s-1) x (1.67 x 10-27 kg) x (1.67 x 10-27 kg) = 18.8 x 10-65
2.89 x 10-30m 2.89 x 10-30
F= 6.5 x 10-35 Newtons
However, the measured attraction between two protons at the femtometer range is 25,000 Newtons.
The Influence of Disorganized Space
The disparity between the calculated and measured attraction between two protons can be resolved by using a chaotic space model. Because of the small diameter of protons or neutrons the order they impose on space can only extend over a very short distance. Moreover, their positions and movement would be influenced by variations in space to a greater extent than large masses. This influence would further disrupt and limit the distance of the organization they create. Because of the uncertainty caused by the changing geometry of space the interaction of these small masses would be best represented by a probability distribution function. An appropriate function would be skewed to the right with attractive force becoming higher the closer the masses are to each other.
The Gamma Probability Distribution Function
The gamma probability distribution is skewed to the right.
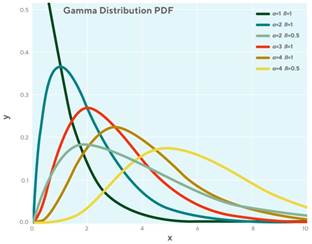
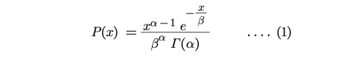
In this distribution when α and β both equal 1 the skewness is like that of Newton’s equation.
By combining the gamma probability distribution with Newton’s law, the magnitude of the calculated attraction is in the range of the measured attraction between small masses that are very close together such as protons or neutrons [2].
F= GM1M2 6.7397 (100r2/β)1-α (e)r2/β + 1/r2
G(α)βα
G is the gravitational constant
M1 and M2 are two masses
r2 is the distance between the center of the two masses squaredy
gamma(a) is the value of the gamma function at a
α=3.46
β=1
Substituting values above using the masses of the protons and a distance r of 1.7 x 10-15meters an attraction of 22,210 Newtons is obtained. This is close to the measured strong interaction of 25,000 Newtons which itself is an approximation (3). At large values of r the term 1/r2 dominates and the gamma distribution function becomes negligible.
Conclusion: This result suggests that there is no fundamental difference between attraction due to the strong interaction and gravity. They are one and the same, both a function of the organization of space by mass.
This interaction exists inside protons and neutrons and mediates the beta decay of these nucleons. Only certain odd and even numbers of protons or neutrons result in destabilization. It is possible that the weak force between masses consists of a disruption of the organization of space caused by imbalanced placement of neutrons and protons that occurs due to their locations relative to each other. This imbalance could result in a change in a or b in the gamma function:
6.7397 (100r2/β)1-α (e)r2/β
Γ(α)βa
For example, increasing a from 3.46 to 5 in the gamma function above would result in a large decrease in the attractive force.
Conclusion: The weak interaction is the result of an arrangement of protons and neutrons that change the gamma probability distribution of space organization thereby reducing attraction due to the gravitational and strong interactions.
Electromagnetic energy can be seen as the cyclical transformation of chaotic to ordered space resulting from the vibration of electrons. The speed of light would be a function of the rate of this transformation. If this rate were constant, then the speed of light would be constant in all frames of reference. When electromagnetic energy passes close to a mass it would enter a region in which space is more ordered and less readily transformed into a waveform. This reduced rate of transformation would reduce the velocity of light and its pathway so that it would bend. This is a phenomenon known as gravitational lensing.
The space around a black hole would be highly organized, so much so, that no light wave could be formed. This prediction is confirmed by using Einstein’s equation for the angle (a) between the pathway the light would have taken had it not been deflected and the new pathway of the light [3].
Einstein showed that a can be calculated using the equation below:
Δ = 4GM/rc2
Δ is the angle of deflection
G is the gravitational constant
M is mass
c is the speed of light r is the distance between
r is the distance between the incident light beam and the center of the mass.
Solving for c one obtains
c= (4GM/rΔ)0.5
Starting with the known angle of deflection of 1.75 arcseconds around the Sun which has a mass of 1.9891 x 10^30 kg one can calculate the angle of deflection and the reduction of the speed of light as mass increases. Using this method, one obtains a speed of light of 0 at a mass on the order of 10^34 kg and an angle of approximately 162,000 arc seconds (45 degrees). Calculation of density yields a density that is of the order of magnitude of black holes.
Conclusion: The organization of space by mass provides an explanation for the bending of light around a mass. This theory also explains the absence of light around a black hole as an inability of light to form. The constancy of the speed of light in all frames of reference is also explained.
Magnetism occurs when the electron spins within a mass are aligned in the same direction. Mass would organize space as previously discussed. But in addition, with the spin alignment a magnet could impose directionality on space so that its curvature or shape at one end is different from its curvature or shape at the opposite end. Attraction would occur between a south and north pole if the shapes of their aligned spaces fit compatibly. If the same poles are apposed, then the shapes would be incompatible and repulsion would result. The strength of this repulsion would increase the closer the same poles are forced together.
Conclusion: Magnetism like the other interactions can be explained as an increase in the organization and orientation of space by a spin aligned mass.
The central idea of this paper is that the gravitational interaction can be made compatible with the other three fundamental interactions by a stochastic model of space that exists inside and outside of mass. According to this model, in the absence of mass or energy, space is changing shape randomly. Mass organizes space through its internal constraints and interactions with space that extend to space beyond its boundary. The greater the distance from the mass the greater the disorder of space. The smaller the mass the greater the effect of the random changes in space would have on its environment. It is also possible that spatial configurations interact iteratively. To describe this stochastic effect on small masses a gamma probability distribution was chosen because with certain values of its shape and scale parameters its shape is similar to that of 1/r2. The addition of the gamma probability distribution function to Newton’s equation for gravitational force extends it to the strong force. A stochastic model of space can be extended to the other fundamental interactions thereby serving as a basis for a theory that subsumes all four of the fundamental interactions. Further work must be done to describe this model mathematically to test this theory and to rule in or rule out the possibility of a substance not yet detected within space that could be the basis of the four fundamental interactions.
- Einstein, Albert (1916) The Foundation of the General Theory of Relativity. Annalen der Physik 354: 769.
- Minkowski, Hermann., Saha, Meghnad (1920) The Fundamental Equations for Electromagnetic Processes in Moving Bodies. In: The Principle of Relativity. Calcutta: University Press 1-69.
- Yousif, Mahmoud (2018) The Grand Unification: 2-The Nuclear (FN) and Weak (FW) Force. RA Journal of Applied Research 4.