According to the theory of supergravity, at the time of Planck (10 -43 seconds after the Big Bang) all four forces of nature (strong and weak nuclear force, electromagnetic force and gravitational force) should have been united in a single super force, i.e. also the strongest (strong nuclear force) with the weakest (gravitational force). Today, the strong nuclear force is 1041 times greater than the gravitational force. The <Cosmic Time Hypothesis> (CTH) now requires that the gravitational constant G, as Paul Dirac already suspected, was stronger in the past than today and steadily decreases over time. Proportionally to G, the gravitational force then also changes. According to the CTH, it would have been greater by a factor of 1041 at the time of Planck than today and thus identical to the strong nuclear force, as demanded by supergravity. CTH also requires that both forces had the same range at Planck time and that the product of range and strength remained constant for both forces until today.
The Standard Model of elementary particles describes the subatomic world. It contains all the fundamental forces except for gravity, which does not seem to fit into the framework. In order to be able to integrate it into the Standard Model, experiments at the LHC particle accelerator are expected to generate new particles, which will then point the way to a new theory that unites gravity with the other fundamental forces (strong and weak nuclear force, electromagnetic force).
The <Cosmic Time Hypothesis> (CTH) follows a completely different path. It assumes a time-variable gravitational force, which leads to the fact that at Planck time (tp ≈ 10-43 seconds after the Big Bang), this force was exactly as large as the strong nuclear force. This is consistent with supersymmetry (SUSY), according to which all natural forces (including the gravitational force) were united in a single superforce at Planck time. The link between the gravitational force and the strong nuclear force also suggests itself because there is a special relationship between the two. Brian Green has already pointed this out, namely [1] " ...that the gravitational force and the strong force have very different properties, but that they have a similar function: Both are necessary for the universe to exhibit certain symmetries. The same applies to the weak and electromagnetic force. Their existence is also tied to certain gauge symmetries."
Linking the strength and range of the gravitational force with the strong nuclear force
The laws according to which the gravitational constant G and the range R of the gravitational force change with time (t) are derived from the <cosmic time hypothesis> (CTH). The result:
G ̴̴ t-2/3, R ̴̴̴ t2/3 (1)
How these relationships come about is described in [2, 3]. Therefore, only a short version is given here. For the Einstein de Sitter universe, the simplest cosmological model for a flat (Euclidean) universe, Einstein formulated the relationship [4],
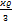 - h2 = 0 (2)
- h2 = 0 (2)
(ϰ = 8πG/c2 = coupling constant of Einstein's field equations, G = gravitational constant, c = vacuum speed of light, ρ = M/V = 3M/4πR³ = mean mass density of the universe, R = world radius, h = 1/ctH = 1/R, tH = Hubble time )
By transforming equation (2) one obtains
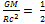 (3)
(3)
Since the Einstein-de Sitter universe expands proportionally to t2/3 [3],
R ̴ t2/3 (4)
if it is postulated that it expands at the speed of light, the following relationship results
Ṙ = 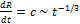 (5)
(5)
This contradicts the postulate of relativity: "The speed of light is a universal natural constant." So what needs to be clarified is: what do we mean by the term natural constant?
Answer: Natural constants are physical quantities that can only be determined empirically and cannot be derived from a higher-level theory. The statement c = constant thus means that the measured numerical value of c must always be the same at any place and at any time. The problem now is to bring this requirement into agreement with the relationship (5).
As we know, Einstein relativised time twice. In special relativity (dependence of time on relative velocity) and in GTR (dependence of time on gravitational potential). The question now arises whether time does not have to be relativised a third time so that the postulate c = constant is also fulfilled for the relationship (5). The task is therefore to find a measure of time that measures the speed of light as a constant quantity at all times, as Einstein recommended [2], p.30: "One can use the principle of the constancy of the vacuum light speed to complete the definition of time." Transferred to the relation (5), the requirement c = constant is fulfilled if one introduces a time τ that changes proportionally to the world radius. An idea, by the way, that Henning Genz already had [4], p. 229: "Why then not go all the way and choose the radius of the universe as the time parameter?"
For the Einstein- de Sitter universe, one then obtains for this cosmic time τ the relation
τ ̴ R ̴ t2/3 (6)
and 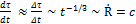 (7)
(7)
In fact, as shown in [3], pendulum clocks and atomic clocks show exactly this cosmic time when they tick according to the laws of CTH. Measured with such clocks, the speed of light is then a constant quantity:
c(τ) = dR/dτ = constant. (8)
The time clock would thus not only depend on the relative velocity (SRT) and the gravitational potential (GTR), but also on time itself (CTH). A comparison of these dependencies is shown in Figure 1.
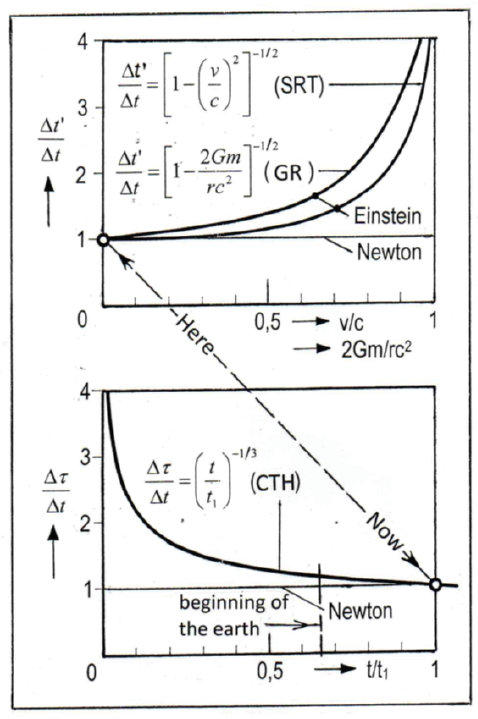
Figure 1: Time relation of SRT, GTR and CTH (t1 = today) [3].
The GTR thus forces us to introduce cosmic time τ in order to bring it into agreement with the equation GM/Rc2 = ½ derived from it. In plain language, this means: The GTR is time asymmetric! It has a cosmological arrow of time and thus follows the 2nd law of thermodynamics.
From the relationship (3), (4) and (5) one obtains
GM = constant (9)
With the assumption that the total energy E in the universe is constant, the following results from E = Mc2 and (5) for the mass of the universe
M ̴ t2/3 ̴ R (10)
Here M means the total gravitationally effective energy existing in the universe (M = E/c2). This includes, in addition to the ponderable mass, also the radiation and
vacuum energy. All these forms of energy are positive, as shown in [3], and are contained in the energy-momentum tensor of Einstein's field equations.
The further relations result from (4), (9) and (10).
Gravitational constant:
G ̴ M -1 ̴ t - 2/3 (11)
Mean mass density of the universe:
ϱ ̴ R -2 ̴ t - 4/3 (12)
Mean energy density:
ε = ϱc2 ̴ t - 2 (13)
One could now object that time-varying "natural constants" (c ̴ t-1/3, G ̴ t-2/3) are not compatible with GTR. However, since c and G do not appear solitary in the field equations, but are linked by the coupling constant ϰ = 8πG/c2 = 1.86 ∙ 10 -26 m/kg, there is no contradiction between GTR and CTH.
From relation (11) it follows for the relation between gravitational force FGP at Planck time (tp = 5,4 ∙ 10-44 s ) and the gravitational force FG1 of today (t1 = 4.3 ∙ 1017 s):
FGP/FG1 = (t1/tp)2/3 = 0,4 ∙ 1041 (14)
This result agrees with the value given in the literature as the ratio between strong nuclear force Fs and present-day gravitational force FG1 [6], [7]. Thus, it holds:
Fs ≈ 1041 ∙ FG1 (15)
and Fs ≈ FGP (16)
The range rs of the strong nuclear force is about 10-15m [6], so it is identical to the range of the gravitational force at Planck time, when the first symmetry breaking of natural forces took place. Thus we get:
Fs ∙ rs = FG ∙ R = constant (17)
Later, the other natural forces also became independent (see Figure 2).
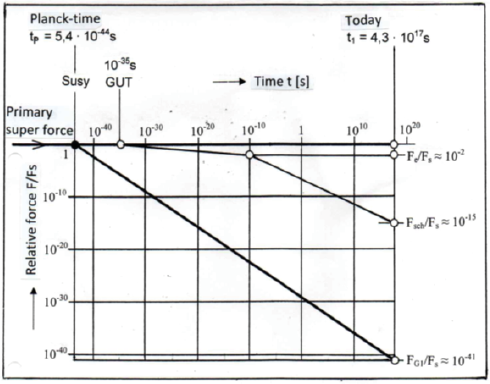
Figure 2: The fundamental forces of nature (Fs = strong nuclear force, Fsch weak nuclear force, Fe = electromagnetic force, FG = gravitational force)
It is interesting to note that according to loop quantum cosmology, the gravitational force at the Planck scale (lp ≈ 10-15 m) is supposed to have had a repulsive effect [8], which is also true for the strong nuclear force (see Figure 3). This similarity between the gravitational force and the strong nuclear force [1] suggests that before the first symmetry breaking (t < 10-43 s) there was indeed a repulsive superforce that could have triggered the expansion of the universe. To quote B. Geene [1]: "The surprising discovery was made that gravitation can be repulsive under certain conditions, and according to the theory these conditions prevailed at the earliest moments of cosmic history. During an interval of time that would make a nanosecond seem like an eternity, the universe offered conditions in which gravity could exert its repulsive effect so violently that each region of space was driven away from every other with tremendous force. The repulsion of gravity was so violent that it not only identified the bang, but it proved to be bigger - much bigger - than anyone had dreamed." Such extreme events could possibly also explain the CTH. It requires that the expansion velocity of the universe (Ṙ = c) was a huge factor of 1020 greater in Planck times than it is today. In order to generate this enormous expansion speed, the primordial, repulsive superforce would indeed have had to have been unimaginably large, which seems quite plausible if one assumes that it had a similar course at that time as the strong nuclear force (Figure 3). In terms of cosmic (real) time τ [2], [3], however, this expansion process took place much more slowly than from the perspective of today's time t.
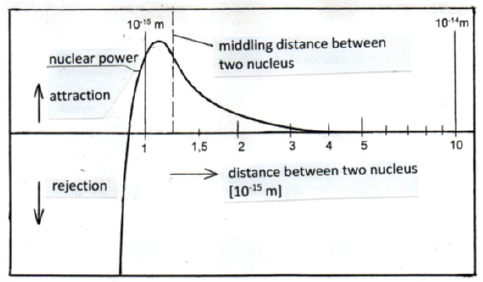
Figure 3: Strength of nuclear forces, depending on the distance of two nucleons from each other (qualitative) [6].
Even if these considerations are rather speculative, they could perhaps build a
bridge between quantum physics and relativity.
- Greene B (2004) The Fabric oft the Cosmos:Time, Space and the Texture of Reality, A.A.Knopf, New York.
- Fritsch H (2019) Die asymmetrische kosmische Zeit. SHAKER-VERLAG.
- Fritsch H, Schlücker E (2020)The Asymmetric Cosmic Time - The Key to a New Cosmological Model. Int J Cosmol Astron Astrophys.
- Einstein A (1990) Grundzüge der Relativitätstheorie. Vieweg 6th edition.
- Genz H (1999) Wie die Zeit in die Welt kam. Carl Hanser Verlag .
- Atkins KR (1976) Physics Third Edition, John Wiley and Sons, Inc.
- Meschede D (2005) Gerthsen Physik" 23. Auflage Springer-Verlag.
- Müller A (2013) Raum und Zeit. Springer Spektrum.



