Abstract

In the spiral galaxies, including the Milky Way, a flat rotation curve V(r) that does not obey Kepler's law was discovered in the early 1930s and became a great mystery. Initially, this could not be explained correctly by Newtonian mechanics, and a hypothesis was proposed that there was a new, unidentified dark matter that increased the gravity. However, there is still no conclusive evidence, although the indirect studies of cosmic background radiation and gravitational lensing effect support this hypothesis. In this study, I focus on the characteristic spiral shape of galaxies and propose a new gravity model (basic equation) based on Newtonian mechanics. This model predicts the existence of a new centripetal force, the interstellar force T(r), which is different from the conventional gravity in the spiral motion. In the verification, an analytical solution V(r) was derived based on the new basic equation and compared with the observed data. As a result, the new model was successfully verified for the first time, agreeing for the entire region from the bulge edge to the solar system with a difference of about ± 5%, including the fluctuation characteristics. It was found that the centripetal force of the disk part forms a new force, "spiral force" by the spiral motion in addition to the conventional gravity, and that these two forces are generated simultaneously in unison. The spiral force is generated by the macroscopic interaction of Universal gravitation between the stars and manifested by the expansion of the scale to the galactic system, and I believe that it represents a new principle for the generation of gravity that does not exist in the conventional concept. I hope that this new gravitational model (gravity theory) will be utilized as a useful tool for the deeper understanding of the spiral galaxies in the universe in the future.

Key Words

Spiral Galaxies; Newtonian Mechanics; Bulge, Disk; Rotation Curve; Universal Gravitation; Gravitational Principle; Centripetal Force; Interstellar Force; Spiral Force; Dark Matter;

Introduction

About a century has passed since the discovery of stellar rotation velocities (rotation curves) in the spiral galaxies, including the Milky Way, that do not obey Kepler's law [1,2].  However, from the viewpoint of the discussion on the rotation curve V(r), I believe that the correct explanation and understanding of the discovery from a unified viewpoint have not been obtained [3-6]. 

In this study, I proposed a "new gravitational model" focusing on the spiral shape based on Newtonian mechanics in order to solve the problem. In order to explain the complexity and difficulty of this problem, I will first review the history of conventional ideas and solutions, and explain how we have come to the present state of knowledge. Then, the contents of the proposed model will be outlined, and the position, importance, and innovativeness of the solution to this problem will be clarified.

The V(r) characteristics of circular motion are derived from the kinematic force balance condition ( basic equation), which is inversely proportional to the square root of the distance  from the galactic center (in accordance with Kepler's law). There was the theory of gravity (basic concept) that the centripetal force balanced with the centrifugal force is only gravity until now. This was also an empirical fact derived from the planetary motions of the solar system, and had become an absolute, common sense truth. However, in the early 1930s, with the improvement of measurement techniques, it was discovered that the stars of spiral galaxies do not follow the characteristics of V(r) obtained from the basic equation, but show almost a flat characteristics [1]. This was a great kinematic mystery and problem. Moreover, the problem is still unsolved even now, more than 90 years later, and exists as "the mystery of the rotation curve" or "the problem of the mass defect" [2,6].

Since this problem could not be explained only by the observed mass data, it was considered to be caused by the lack of mass based on the basic equation. Therefore, it has been assumed from the beginning that a new type of invisible matter called dark matter (= unknown elementary particles?) is involved [9]. The explanation (hypothesis) that dark matter increases the gravity (mass) seemed to solve the problem for a while. However, although many years have passed since this hypothesis was proposed, dark matter has not been discovered yet. Recently, it has been pointed out that there may be a fundamental problem with this idea of dark matter [10,11]. 

In contrast, the new theories such as the modified Newtonian mechanics [12] have been proposed to address this problem. However, the contradictions have been reported in these theories. Furthermore, an attempt was made to determine the mass of the disk by an optical mean alone, regardless of the basic equation of V(r). [13] This attempt is aimed at explaining the flat property of the disk with respect to its mass and at a new understanding. The mass is obtained statistically from the mass/luminance ratio (M/L), which converts the luminance L to the mass M. However, there were the problems with the accuracy of this method and its application to the invisible material [7,14].

There was also an attempt to obtain the analytical solution from a potential theory. Miyamoto and Nagai (MN) model was newly proposed based on the idea that the factor of gravity (mass) increase exists in the disk of the galactic plane. [15] However, the masses and the distributions of the bulge and the disk obtained from this model did not give the flat characteristics for the entire galactic region. The outer regions of the galactic plane could not be explained, and the existence of dark matter was inferred to be necessary [9].

Let us now focus on dark matter as the current mainstream model. The purpose of this model is to discover the unknown matter (e.g., elementary particles) with a new mass distribution that increases the gravity based on Kepler's law. From a different point of view, instead of trying to understand the flat characteristics of the observational data itself, it shifts the challenge to the discovery of unidentified dark matter, which is one of the hypotheses. This is mainly owing to the fact that for a long time the observed characteristics have not been well explained in kinetic terms. As explained in Section 2 below, dark matter is basically configured to fit the observational data. There is a degree of freedom in its properties and mass distribution, and no problem arises at the introduction stage. Dark matter has now been narrowed down to its properties and location, and its coverage has been extended to the halo region surrounding the spiral galaxies. This is called the dark halo.

The dark halo is supported as one of the factors that increase the gravity, as shown in the paper on the gravitational lensing effect . Furthermore, the observations suggest that about  of the universe is composed of dark energy and dark matter, which forms the background for understanding the universe as a whole. Based on these circumstances, the Milky Way is considered to be composed of three major components: a bulge containing the black holes and the central core, a spiral disk surrounding the bulge, and a huge dark halo (dark matter) enveloping the entire galaxy [8,17].

As mentioned earlier, the switch in the target of the problem (issue) has led to the misunderstanding that the mystery of the V(r) characteristics has been solved. Nowadays, as can be seen in research publications, the direction of the issue has almost shifted to the search for dark matter worldwide, and observations, measurements, and theoretical developments toward its discovery are being actively carried out [10,18].

In this way, it can be said that the research flow has been basically narrowed down to the search for and discovery of dark matter, owing to the absolute existence of Kepler's law (gravity theory) based on experience and the observation results that are considered to be caused by the increase in gravity.

However, if we face the fact that Kepler's law does not hold, there is a possibility that a "new theory of gravity" may exist, and there is a risk that dark matter will not be discovered [11].

The aim of this study is quite different from the previous attempts to discover dark matter. I focus on the observational data of V(r), which is the origin of the mystery, and aim to derive the new basic equation (the balancing condition) that can be explained in terms of the kinetic theory. This will simultaneously lead to the search for a new theory of gravity in Newtonian mechanics. Unlike the solar system, the spiral galaxies have a characteristic spiral shape and motion. This feature is considered to be a necessary condition for the stable rotational motion of stars in the spiral galaxies. By clarifying this point kinematically, I believe that the new physical phenomena (generation of force by the spiral motion) will be found, which have not been predicted so far.

In Section 2, the new basic equation is predicted kinematically and geometrically from this point of view, and the new gravity model for the spiral motion is proposed. In Section 3, the analytical solution V(r) of the rotation curve is derived from this basic equation, and is compared and verified with the observed data. As a result, the validity of the model is confirmed, and at the same time, a new force, which does not exist in the conventional concept of gravity, is found. I believe that this force is caused by a "new principle (theory) of the generation of gravity" in Newtonian mechanics [11].

In this study, while verifying the new gravity model as described above, V(r) characteristics are analyzed and evaluated to physically support the model. And many important findings are obtained as well as solving the mystery of the spiral galaxies.

New Gravity Model

In this Section 2, I propose a new gravity model based on Newtonian mechanics, focusing on the spiral motion (shape) by the observational data of the Milky Way.

Approach of model

According to the observational data of the Milky Way, the stars including our solar system are in the stable circular motion while maintaining the spiral shape as a whole. When analyzing this motion, there are two types in the features. One is the circular motion of stars around the galactic center, and the other is the spiral motion of stars (group of stars) that is simultaneous with the circular motion. The main feature of the new model is that these two types of motions are considered separately. Therefore, the motion region of the new model basically covers only the interior of the two-dimensional spiral arms that form a stellar population in the spiral galaxy. In contrast, the conventional model covers the three-dimensional space of the entire spiral galaxy (in particular, it does not distinguish between the interior and the exterior of the spiral arms), which is significantly different from the new model.

Conventional model

Figure 1 shows the conventional model of circular motion. It is also the circular motion shown by the planets in our solar system. This is a vector diagram showing the equilibrium condition between the gravitational force F by the central mass M and the centrifugal force f with respect to the stellar mass m. The basic equation is given by the equation (1), which is conventionally considered absolute [8].

(GMm) /r² = m. (V²/r) (1)

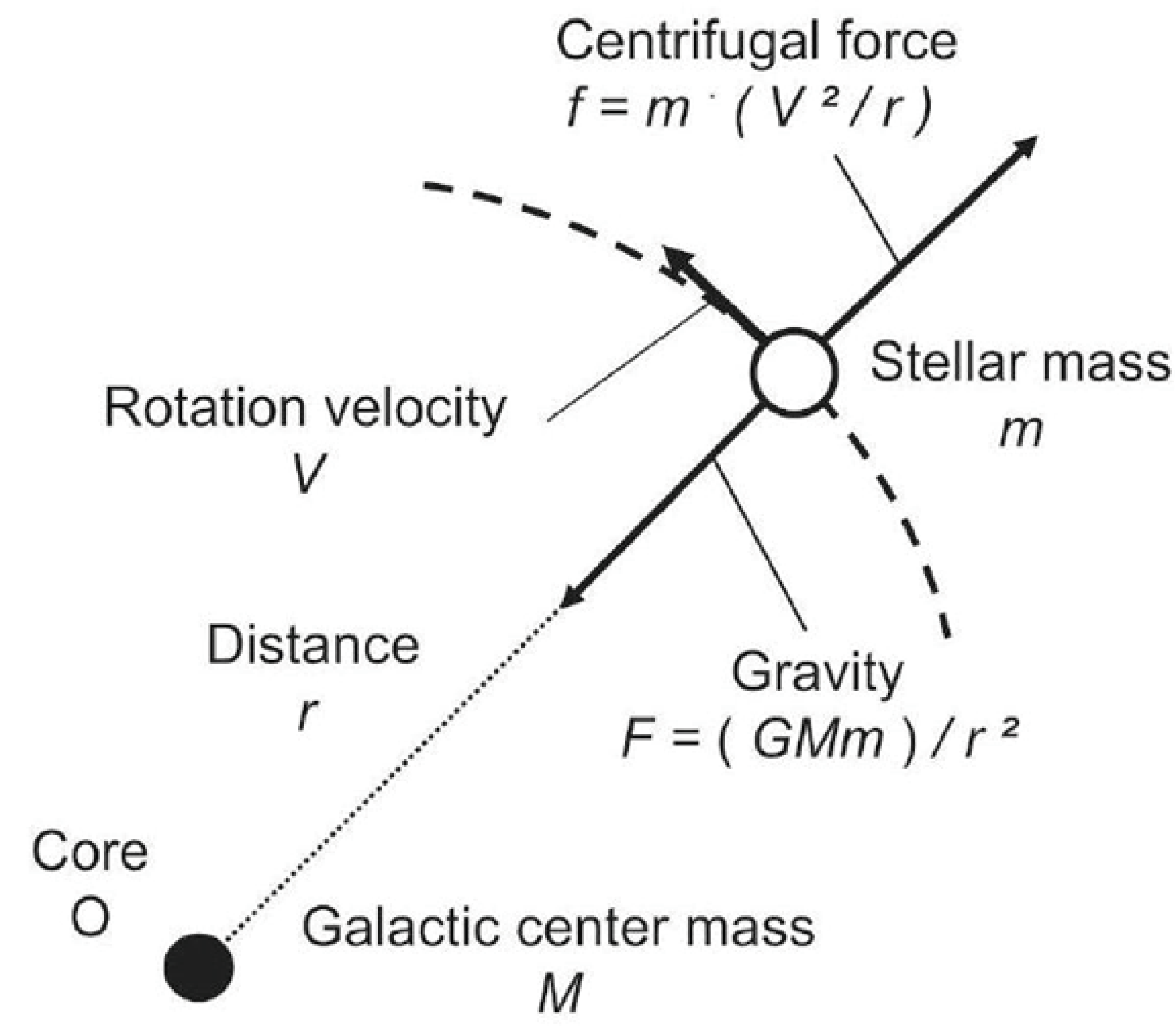
Figure 1: Conventional model of circular motion

Similar to the planetary motions in the solar system, the region of motion covers the three-dimensional space where the gravity F acts. In contrast, the right-hand side of equation (1) is the centrifugal force ƒ, which indicates the two-dimensional balancing condition with respect to the star.

In this basic equation, the existence and necessity of another spiral shape (motion) exhibited by the stellar population has not been specifically considered.

This is because it was thought that even if one circular motion exhibits the characteristics of two motions, they are kinematically identical.

The observation data of spiral shapes have been discussed using various parameters based on the logarithmic spiral shape, including the measurement method. However, there is no particular attempt to reconsider kinematically the features of the spiral shape in relation to the V(r) characteristics [19]. Equation (1) has been used as the kinematic balance condition for the stars as well as the planets in the solar system. From this equation, the V(r) characteristics of star moving in a circle are given by the following equation (2). In most cases, the conventional models consider this equation (2) as a starting point (precondition).

V(r) = (GM / r) ^½ (2)

However, the V(r) data observed in the spiral galaxies did not decrease with increasing the distance r, but showed almost the flat characteristics. The disk mass M_d at this time means the real measurable mass. However, the flat characteristics could not be obtained even when the M_d was taken into account to increase with the distance r. To explain this discrepancy, the balancing condition in equation (1) itself was not questioned, and the mass M in equation (2) was considered to increase. The kinematic acceptance of this idea is a major difference from the new model, which will be discussed later in Section 2.1.2.

The mass M is given as the center-of-mass, which is the total mass M_t (= M_b + M_d) of the bulge mass M₀ (= M_b) at the center of the spiral galaxy and the disk mass M_d surrounding it. The two masses were predicted as the real masses by the conventional methods, but they did not show any increase in the missing mass.

Therefore, the mainstream model assumes the existence of unidentified "dark matter" to explain the cause of the mass increase [6]. This model explains the V(r) characteristics by adding the dark matter mass Mm (r) to the conventional total mass M_t (= M) in order to increase the gravity. However, the distribution of M_m (r) can satisfy the necessary conditions for fitting the observed data, but not sufficient if the balancing condition in equation (1) is problematic. Therefore, in order to verify this model, the existence of dark matter must first be discovered by the observation, and then the mass distribution M_m (r) must be confirmed. However, no evidence of the existence of dark matter has been found for a long period of time up to the present day.

Construction of new model

In contrast, the new model focuses on the spiral shapes (motions) of the galaxies, which have not been specifically treated in the conventional model.

Considering the necessity of the characteristic spiral shape and structure, the balance model presented in equation (1) was reconsidered from the kinematic point of view. The following is the idea, in which the physical phenomena (a new gravity model) are considered on the basis of Newtonian mechanics from the present situation of the spiral galaxies.

Apart from the gravity generated by the center-of-mass of the disk, the stars interact with each other by Universal gravitation between the neighboring stars.

Usually, the collisions are likely to occur when the stars are grouped together, but the spiral galaxies maintain their spiral shape as a whole (rigid body motion) and have the stable rotational motion. In other words, the stars have acquired the motion that maintains a constant spacing between the stars in spiral motion, and have stabilized. It is inferred that a new force (macroscopic force caused by the interaction between the stars) is generated inside the grouped spiral arms to maintain the stable motion, in addition to the gravity (centripetal force) that maintains the circular motion.

The new force in the spiral motion is considered to be the driving force that stabilizes the circular motion of the stars and generates the force along the shape of the spiral (tangential force). This macroscopic force is hereafter referred to as the "interstellar force T". The force T generated on the disk forms the new circular orbit and rotational velocity because the circular motion simultaneously behaves as the spiral motion. Therefore, the interstellar force T is inferred to have the characteristics of both the gravity F of the disk and the new force.

Furthermore, the characteristic of this force T is that, although it includes the gravity F of the disk, the other new force depends basically on the interstellar distances inside the spiral arms and is not directly affected to the decay with respect to the distance r (scale expansion) from the center of the galaxy.

Therefore, among the interstellar forces T, the new force is expected to affect the flattening of the V(r) characteristics.

Figure 2 is the diagram of the "new gravity model of the spiral motion" proposed based on the above ideas. The average spiral arm shape, which is called the logarithmic spiral shape, is represented by a single dashed line (the center line), and the balancing condition of the interstellar force  is shown by the vector diagram.

The interstellar force T is generated in the tangential direction of the spiral shape shown by the dashed line in Figure 2, and acts as a macroscopic force on the stars in the spiral arms.

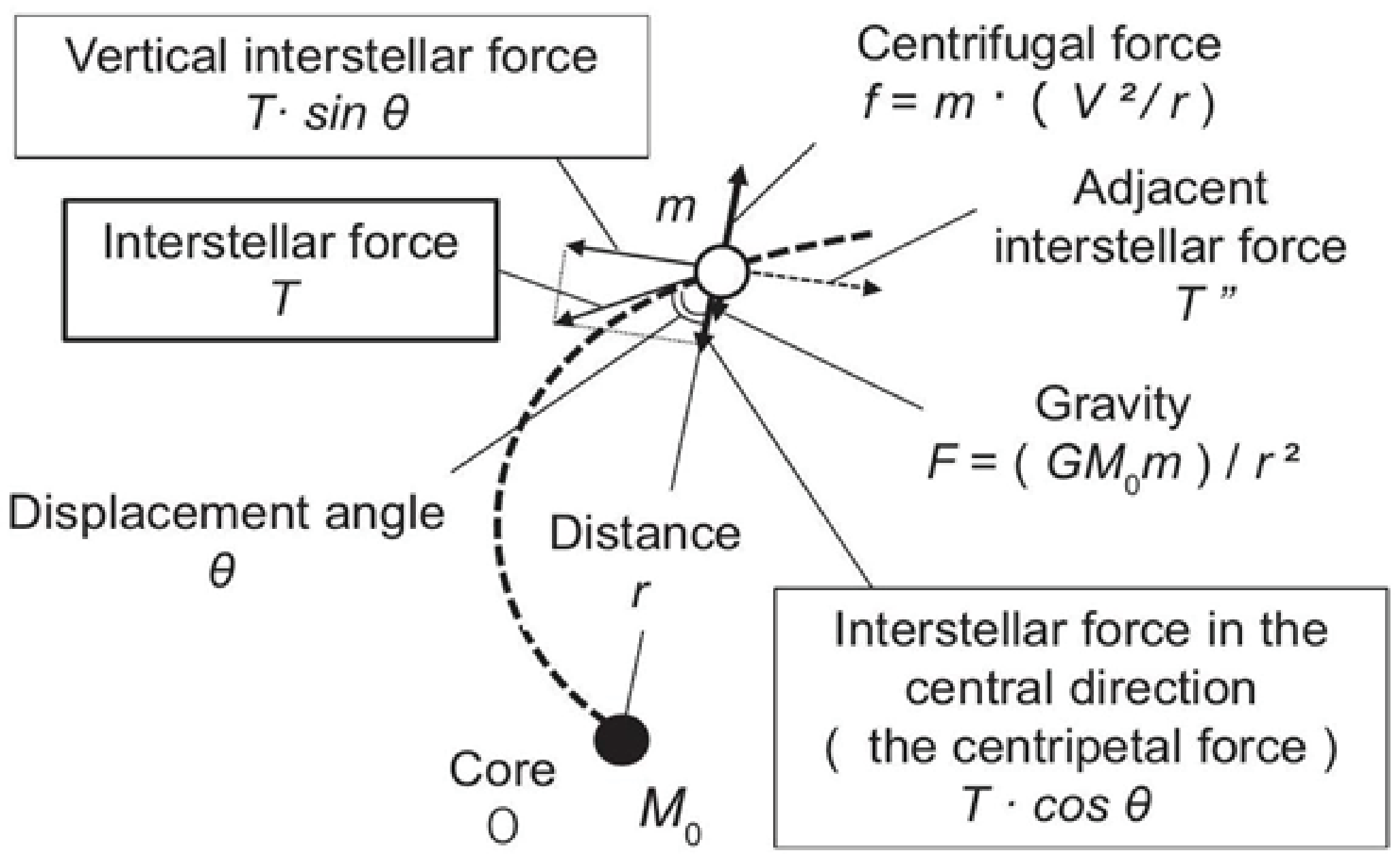
Figure 2: New gravity model of spiral motion.

The displacement angle  represents the angle of shift from the vector of the interstellar force T to the center direction, and is related to the pitch , which indicates the logarithmic spiral shape parameter, by . The relation of the logarithmic spiral is discussed in equation (7) of Section 2.2.

This force T can be geometrically divided into two vector components based on its function, as shown in Figure 2. One is the centripetal force, which is necessary for the stable circular motion of the grouped stars and is added to the gravity of the disk as a new force. This force is the component toward the center of the spiral galaxy and is given by . The other force, which is necessary to maintain the macroscopic spiral motion (shape) as a whole, is the binding force that forms a new orbit and connects the neighboring stellar population. This force is the component orthogonal to the generating direction of gravity, and is given by.

Now let consider the external case of the spiral arms, in which the interstellar force  does not act. Since there is no interaction between the stars, the conventional gravity model is basically valid as in the case of single motion.

However, since the stars are not affected by the interstellar force T and thus cannot acquire the new orbits or the rotational velocities, the motion is considered to be irregular (i.e., they are entangled in the neighboring spiral arms). As a result, it is inferred that the star is in a transient state of motion outside the spiral arms.

Consequently, the stars cannot or will not exist in the outer regions, so they will move to the more stable inner regions of the spiral arms or the bulge. From this point of view, the region of stellar motion in the new model is basically limited to the interior of the spiral arms in two-dimensional space (the galactic plane), as described in the first discussion. It can be inferred that most of the previous observational data obtained in the past have targeted (selected) the interior of the spiral arms, where there are many stars. The reasons for this are that the stellar data observed by the conventional model is considered to be unaffected by the positional relationship with the spiral arms, and that there were few stars to be measured outside of the spiral arms. The observational data showing this can be found in the paper by Rubin et al [14].

From the above, the new gravity model for the spiral galaxies has three main features.

1. The two-dimensional macroscopic interstellar force component (T ^. cos θ), which is a new concept, exists as the centripetal force balanced with the centrifugal force .
2. There exists the interstellar force component T ^. cos θ that binds the adjacent stellar populations together to form the spiral motion (rigid body motion).
3. The stellar motion region is interior of the spiral arms in the galactic plane, which is different from the conventional model.

From the first feature (1), the new gravity model (basic equation) of equation (3) can be obtained kinematically, in which the centrifugal force f is balanced with the two forces, namely, the conventional gravity of the bulge plus the centripetal force T ^. cos θ of the disk part.

T ^. cos θ + (GM₀ m) / r² ₌ m ^. (v² /r) (3)

Until now, the centripetal force that is balanced with the centrifugal force ƒ has been conceptually considered to be only the gravity F. However, in this model, the addition of the newly predicted centripetal force component T ^. cos θ (including also the gravity at the disk) changes the conventional basic equation for the first time. Comparing the left side (centripetal force) of equations (1) and (3), respectively, the gravity F by the mass M corresponds to two terms: the gravity F by the bulge mass M₀ and the centripetal force T ^. cos θ related to the mass M_d of the disk section. In this case, the latter centripetal force T ^. cos θ includes two forces together, consisting of the gravity by the real mass in the disk and the new force generated by the spiral motion ("new centripetal force"), based on the aforementioned idea of the interstellar force T. The reason for the unification of the forces is that the existence of the stellar mass (gravity) and the spiral motion of the star (new centripetal force) are occurring by a single circular motion.

However, this new centripetal force is generated in a completely different way from the conventional gravity, and requires a new way of thinking and handling. For the sake of further discussion, the two forces are replaced by the disk mass M_d ( = M_d1 + M_d1 ), which consists of two masses M_d1 and M_d2, respectively. The mass M_d1 is the conventional measurable real mass (the mass treated as the center-of-gravity mass), which generates the gravitational force F.

On the other hand, the mass M_d2 is the mass corresponding to the new centripetal force, and is given as a hypothetical mass converted to the gravity equivalent by bracketing its force with the functional form of gravity (r -²). This mass is to compare the magnitude of the new force with the gravity, and does not imply the occurrence of gravity in the physical phenomenon. Thus, the centripetal force T ^. cos θ in equation (3) can be related as the gravity consisting of two masses, the mass M_d1 (real mass) and the mass M_d2 (hypothetical gravity-equivalent mass).

Next, another feature (2) will be discussed in relation to the interstellar force T. In the Milky Way, according to the observational data [19], there exist two pairs of the spiral arms, which are thin disks and nearly point-symmetric with respect to the center of the galaxy. Each spiral arm has multiple spiral arms and maintains the complex stable state.

When incorporating the spiral shape effect (interstellar force T) in the new model, the balancing condition is simplified and one spiral arm is indicated by the center line. As in the case of equation (1), the basic equation in equation (3) is expected to be applicable to the complex spiral shapes that preserve the symmetry and stability of the entire galaxy. The force that maintains the spiral shape is the force T ^. Sin θ, which is the coupling force component necessary for the spiral motion shown in the feature (2). This force is geometrically bounded by the force T" of the neighboring stars (group) in order to achieve the force balance in the connected state shown in figure 2. From this, the basic condition for forming and maintaining the spiral shape is given by the equation (4). This relation is needed in the functionalization of the interstellar force T, which is embodied in the next Section 2.2.

T ^. Sin θ = T" (< T) (4)

From the above, by introducing the interstellar force T, it is shown that the gravity model of the spiral motion has two new balancing and constraint conditions as shown in equations (3) and (4). After this, proceeding to the verification of the rotation curve V(r) derived from the basic equation, the first step is to functionalize the interstellar force T (r) predicted by the model.

Functionalization of the interstellar force

In this section, the force T (r) generated in the spiral shape is related to the function of the distance ^r based on equation (4). Figure 3 shows the discretized vector diagram of the force T (r), taking into account the constraints of the spiral geometry.

Figure 3 depicts the case where the displacement angle θ  is 60° (pitch ΔΦ = 30°) as an example to illustrate the constraint condition in equation (4). The initial value T₀ is given by the bulge end r₀ (the rigid sphere of mass M₀ and radius r₀), which is the starting point of the spiral (n = θ). The bulge end r₀ is obtained from the observational data treated in Section 3 below. The graded equation (5) for the discretized interstellar force T_n is obtained from the constraints in equation (4) based on Figure 3.

T_n = T_n-1. sin θ (5)

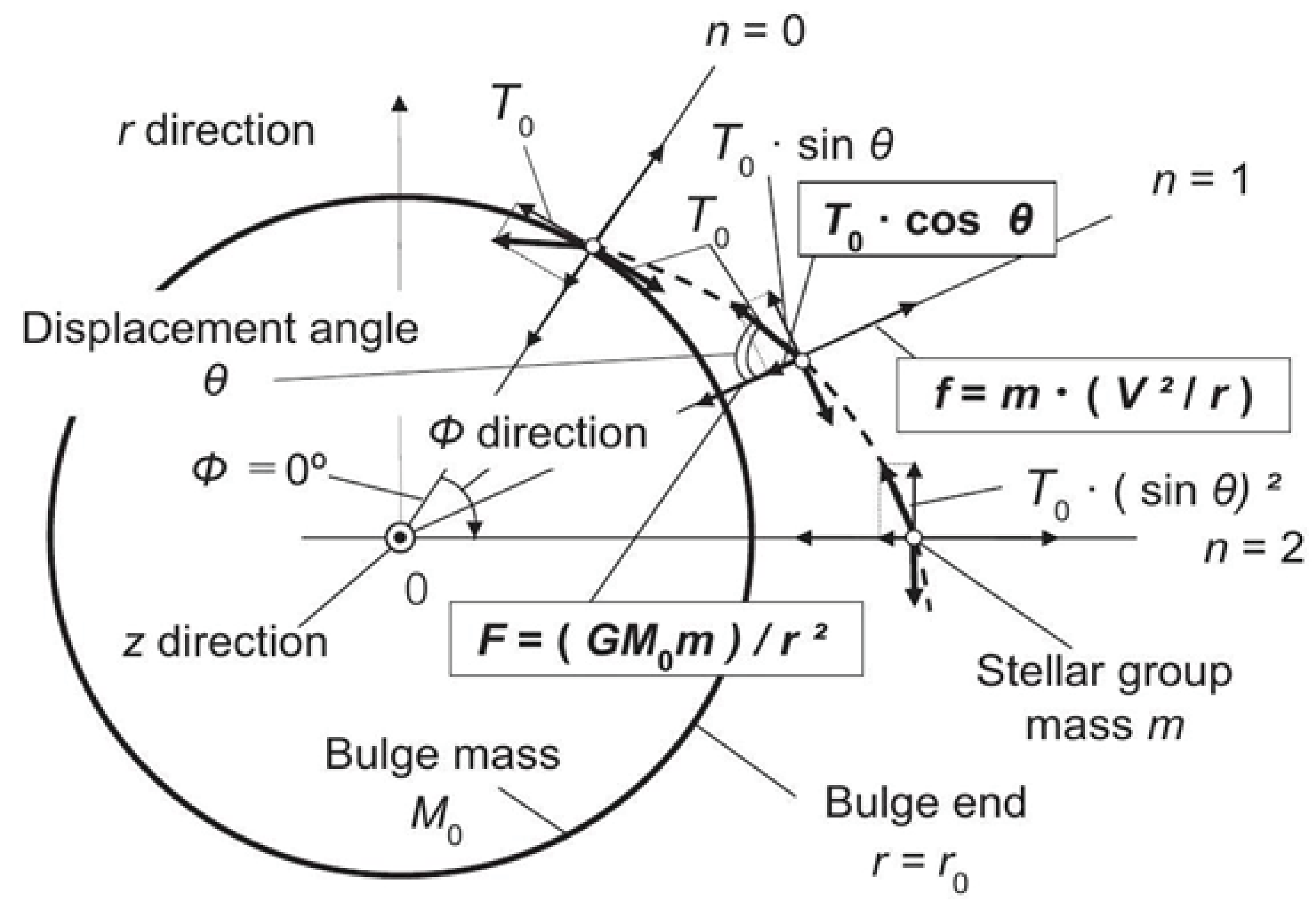
Figure 3. Vector diagram showing the balancing and constraint conditions when T is discretized. This figure shows an example when the displacement angle is θ = 60° and the pitch is ΔΦ = 30°. Furthermore, the initial value of force T₀ is given by the radius r₀ of the bulge edge where the spiral is generated. By repeating this graded equation, equation (6) can be further obtained.

T_n = T₀ ^.(sin θ)ⁿ (6)

T_n can be obtained using the graded equation (equation (6)), but the displacement angle θ, or the pitch ΔΦ, is constrained by the discretization condition as shown in the vector diagram in Figure 3. It is necessary to discretize T_n  for each pitch ΔΦ with respect to the rotation angle Φ. Furthermore, it is necessary to eliminate n in the reduction equation, and the distance r_n after the discretization shown in equation (7) is used from the relation of the logarithmic spiral geometry.

r_n = r₀ ^. exp (α ^. Φ_n) (7)

The coefficient α is the aperture ratio of the logarithmic spiral, a parameter that represents the aperture state with respect to the rotation angle Φ and is independent of the pitch ΔΦ. This value is obtained from the observational data in Section 2.3.1 below.

From the above, the functional form of the interstellar force T(r) is given by equation (8), using the discretized form of equations (6) and (7).

T(r) = T₀ ^. (r/r₀)α (8)

where α is the newly introduced "spiral exponent", which is expressed as a function of the spiral shape (α, ΔΦ) and is given by equation (9). The initial value of T₀ and the bulge radius r₀ are given by the fittings and the observed data in Sections 3.1 and 3.2.

α (α, ΔΦ) = [in (cos ΔΦ)] / (α ^. ΔΦ)

where α < 0. In particular, the unit of the pitch ΔΦ used in equation (9) is radians (rad), not degrees (°). (9)

Parameters of logarithmic spiral shape

In order to obtain the T (r) shown in equation (8), the value of the spiral exponent α in equation (9) is required. Therefore, the aperture ratio α and the pitch ∆ф are first obtained from the observed data of the spiral shape.

Aperture ratio

The aperture ratio  is obtained from equation (7) by using the slope of the distance ratio  r/r_0i to the rotation angle ф in equation (10).

Log (r/r_0i ) = (log e) · α · ф (10)

Figure 4 shows the relation between the rotation angle ф and the ratio of the distance r/r_0i from the galactic center based on the observed data. The spiral shape data of the Milky Way is directly read and plotted [19]. No.1, No.2, No.3, and No. 4 in the figure are representative spiral arms, which are called Norma Cygnus, Perseus, Sagittarius-Carina, and Scutum-Crux, respectively.

The distance r_0i is defined as the position where each spiral arm (No. i, i = 1, 2, 3, 4) appears from the center in the observed data, and the rotation angle ф = 0 at this point.

The distances r_0i all correspond to the distance r₁, which will be discussed in Section 3.1 below, and are particularly noteworthy in relation to the observed data.

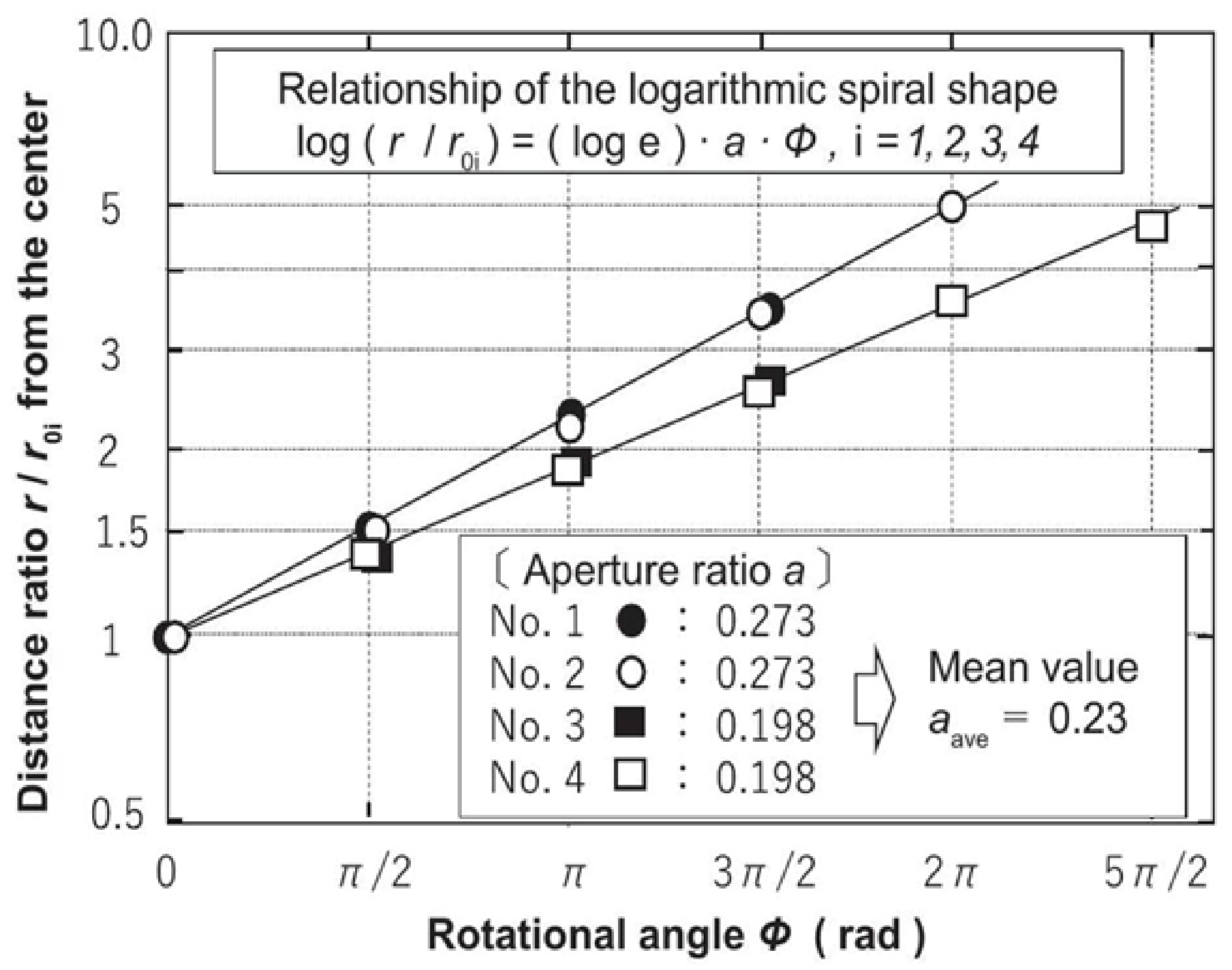
Figure 4: Relationship between the rotation angle ф and the distance ratio r/r_0i of the Milky Way. The aperture ratio α is calculated from the spiral shape data using equation (10). The distance r_0i is defined as the position where each spiral arm (No. i, i =1,2,3,4) appears from the center using the spiral shape diagram of the observational data [19], and the rotation angle ф = 0 is set at this point.

In Figure 4, the slope of the graph is indicated by a straight line, thus confirming that the spiral galaxies have the logarithmic spiral shape. In this case, each pair of spiral arms of No. 1 and No.2, and No. 3 and No. 4 are said to be point symmetric with respect to the center of the galaxy. However, from the slope of the graph, the aperture ratios α of the pairs No. 1 and No.2, and No. 3 and No. 4 are different from each other, 0.273 and 0.198 , respectively.
Furthermore, the values of pitch ∆ф, which have already been examined in the literature data, [19], are also different, being 15⁰ and 11, respectively.

The values of both parameters α and ∆ф of the spiral shape are significantly different for the different pairs, while they coincide each other with high accuracy for the same pairs. This means that the spiral arms can remain stable in each case even if the spiral shapes of different pairs are different from each other. Here, when the functional form of the spiral exponent α in equation (9) is examined, the aperture ratio α and the pitch ∆ф are also found to have the opposing relationship. From these results, it is possible that the spiral galaxy has a kinematic balance that keeps the exponent α, i.e., the functional form of the interstellar force T (r), constant. Here, the average of two sets of the aperture ratios , i.e., α_ave = 0.23,  is adopted and incorporated into the function of T (r) as the characteristic of the spiral arms. The point where the parameters α and ∆ф can be treated as average values is explained in Section 4.4.2 below. Having obtained the aperture ratio α_ave, the next step is to examine the relation of the exponent α to the pitch ∆ф.

Relationship between pitch and spiral exponent

Figure 5 shows the relationship between the pitch ∆ф and the spiral exponent |α| using equation (9).

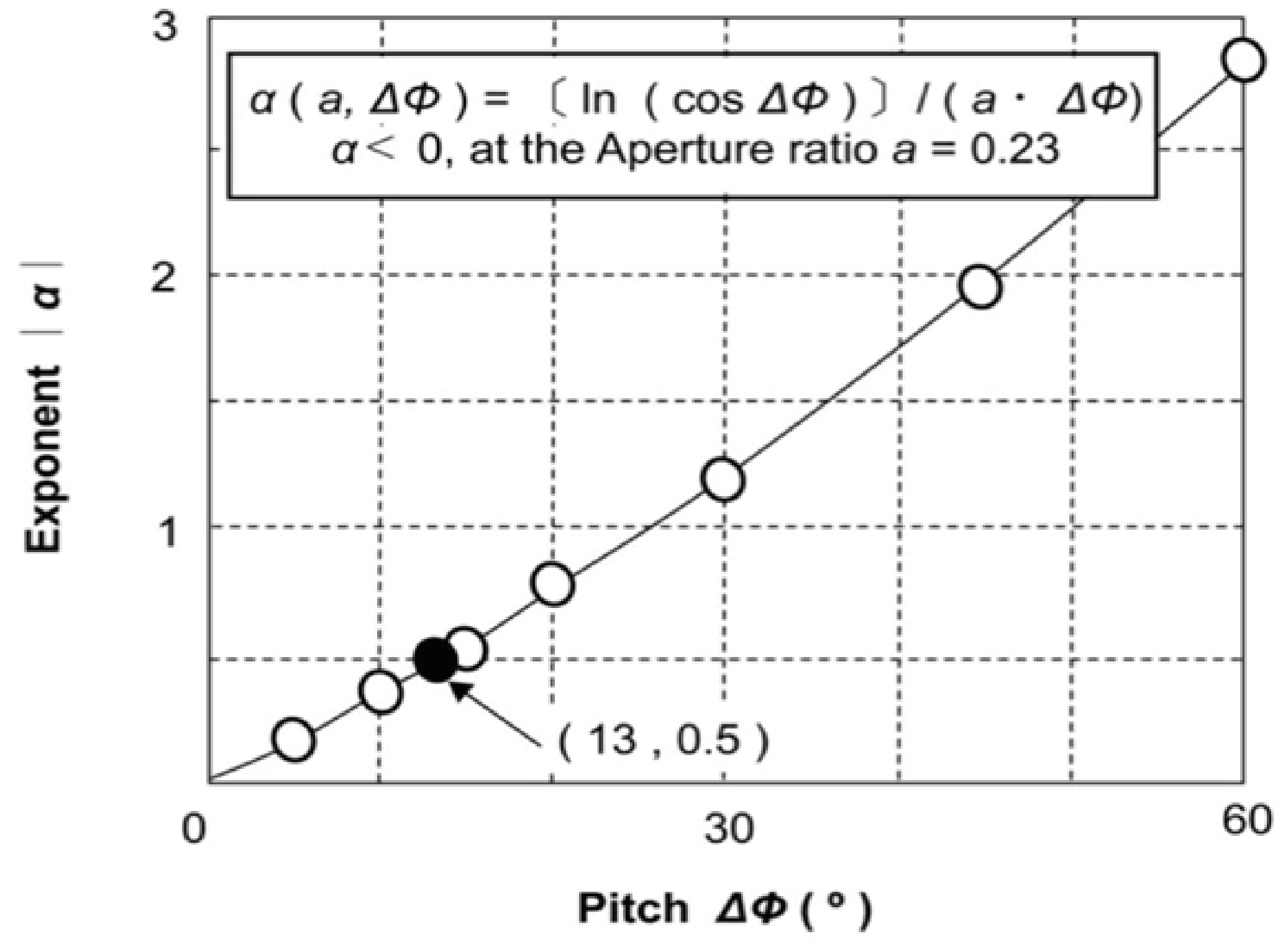
Figure 5: Relationship between pitch ∆ф and spiral exponent |α|.

As mentioned above, in the spiral exponent α (α, ∆ф) shown in Figure 5, the unit of pitch ∆ф is expressed in radians, but in the plot of the graph it is expressed in degrees (display of observed data). The exponent |α| shows a simple increasing function with respect to the pitch ∆ф when the aperture ratio α is constant.

Although the pitch ∆ф has two different values in the spiral arms, the average value ∆ф_ave =13⁰ is used as in the case of the aperture ratio a. [19,20] As a result, the value of the exponent |α| is obtained to be about 0.5 from Figure 5, and this value is adopted. The value of the exponent  obtained from the spiral shape determines the T (r) and affects the characteristics of V(r). From this, it is confirmed that the interstellar force T (r) shows a functional form proportional to the distance  r ^–1/2 from equation (8), and that it decays more slowly than the distance r ^–2 of the gravity F (r).

Therefore, it can be inferred that the aperture ratio α and the pitch ∆ф indicated by the observed data of the spiral shapes, together with the spiral exponent α, are the important parameters for understanding the characteristics of the spiral galaxy. The properties (universality and characteristic value) of the exponent α will be discussed in Section 4.4.3.

Derivation and Verification of Rotation Curve

In this Section 3, the analytical solution of the rotation curve V(r) is derived and compared with the observed data. Then, the flattening of the V(r) characteristics is confirmed, and the validity and correctness of the new gravity model is verified. Furthermore, in the next Section 4, based on these results, the physical characteristics and properties of the spiral galaxies will be elucidated using the obtained analytical solution as tools.

Derivation of rotation curve

The rotation curve V(r) is given by equation (11) from equations (3) and (8) in Section 2.

V(r) = [r · T(r) · cos θ/m + (GM₀) /r]^1/2  = [A·r^1/2 +(GM₀) /r]^{1/2 (11)}

There are two unknowns in the V(r), consisting of the coefficient A shown in equation (12) and the bulge mass M₀.

A = r₀^1/2 · T₀ ·cos θ/m(12)

Next, in order to determine these unknowns, the fitting with the observed data is performed. Usually, it is necessary to have the V(r_i) data at two points r_i (i = a, b).

However, in this case, as shown in equation (11), the function has a unique functional form with respect to the distance r, and there exists a local minimum (minima). This is caused by the combination of the increasing function in the first term and the decreasing function in the second term. Although the existence of this minimum has been confirmed by many observations as described below, this is the first time that it could be predicted on the kinematic ground.

From the condition that gives the minimum, a new relation involving the unknowns is obtained by equation (13).

dV (r) / dr = 0 (13)

By using this relation, the fitting can be done at a single point of the minimum value instead of any two points. Furthermore, the unknowns can be related to the parameter of the characteristic minimum, which improves the visibility. As a result, by using one point of the minimum V(r₁) = V_min for the fitting, two relational equations, equations (14) and (15), are obtained.

r₁ = (2GM₀/A)^2/3 (14)

V_min = (Ar₁^1/2 + (GM₀) /r₁)^1/2 (15)

From the above, the unknowns of mass M₀ and coefficient A in equation (11) are given by equations (16) and (17), respectively.

M₀ = r₁· v_min²/ (3G) (16)

A = 2GM₀ /r₁^3/2 (17)

The minimum values (r₁,V_min) adopted for the fitting were specifically those read directly from the observed data of V(r) (2.7kpc, 192 km· s^–1) [3].

The observational data for the V(r) characteristics of the Milky Way have been obtained by a number of measurement methods, [8], but their accuracy is presumably not well evaluated. [14]. The major reason for this is oferred that the flattening problem of the V(r) characteristics has not been solved. Therefore, the observation data, which mainly consisted of the H₁ radiation that has been widely used since the beginning, was selected. The observed data have a local minimum predicted by the present analytical solution and show gradual change in the neighborhood of the minimum. [3,8]. However, the characteristics of the minimum have not been discussed much. Among them, the data studied by Gunn et al. (1979) has a clear minimum of the V(r) characteristics and high reading accuracy, and thus this data was adopted as the data for fitting at a single point [3,5]. This observed data is also used to validate the V(r) characteristics in Section 3.4.

Although the unknowns of mass M₀ and the coefficient A are usually given numerically, here it is possible to treat the parameters of the minimum value as special points (r_1, V_min), and thus to relate them kinematically as shown in equations (16) and (17). As a result, the following two important findings are obtained from the series of relations.

One is that the bulge mass M₀ is obtained immediately when the minimum value is selected as the fitting data. This indicates that the bulge mass M₀ (=M_b) can be estimated kinematically from a single point of the observed data.

This relation shows that the transition of V(r) characteristics can be predicted by the changes in the spiral shape and so on, when the minimum value (r_1, V_min) varies with a constant bulge mass M₀. This point will be discussed in Section 4.2.

The following equation (18) shows the value of the bulge mass M₀ obtained directly from equation (16).

M₀ = 1.54 ×10⁴⁰ kg
        = 0.77 ×10¹⁰ M₀ (18)

M₀ is the mass of the Sun, i.e., 2.0 × 10³⁰ kg. The value of the bulge mass M₀ has the same number of digits as those obtained so far and does not differ significantly.

Furthermore, transforming equation (16) from the viewpoint of kinematics, the following relation is also obtained

v²_min/r1 = 3GM₀/r₁² (19)

At the minimum value of the rotation curve, the centrifugal force f is equal to three times the bulge gravity F, indicating that the centripetal force T · cos θ is twice the bulge gravity F. The existence of the minimum not only gives the bulge mass M₀, but also has the important kinematic implications.

Another important point is that the coefficient A is related to the bulge mass M₀. This indicates that the interstellar force T is related to the mass through the bulge mass M₀. These findings are discussed separately in Section 4.1. Thus, by analyzing the minimum, two important relations (findings) can be obtained. Note that there may be the cases where the minimum does not exist, which will be separately discussed in Section 4.4.

From the above considerations, the analytical solution of the V(r) characteristics expressed in equation (20) is finally obtained. This means that, by giving either the distance r or the value of V(r), the other can be obtained.

V(r) = (GM₀/r₁)^1/2 · [2(r/r₁)^1/2 + 1/ (r/r₁)]^1/2(20)

where r ≥ r₀, r₁ =2.7kpc, M₀ = 0.77 ×10¹⁰M., G = 6.7 × 10^-11 m³ · kg^-2 · s^-2, and the value of (GM₀/r₁)^1/2 is  111 km · s^-1 .The value of r₀ at the bulge edge is obtained from the observed data V₀, which will be discussed in Section 3.2.4. In particular, focusing on equation (20), the V(r) characteristics can be estimated only by the minimum value (r₁, V_min), considering the fact that the bulge mass M₀ is related to equation (16). In Section 4.2, the physical properties and characteristics of the minimum will be discussed based on the verification results.

Estimation of physical quantities

In this section, before examining the overall characteristics of V(r), the characteristic physical quantities of the Milky Way are estimated using equation (20).

Rotational velocity at the outermost

The rotation velocity V₃ is an important parameter in determining the total mass M_t of the galaxy. Using the outermost distance r₃ = 15kpc, [20,21] the rotation velocity V₃ = 246 km._.s^-1   is obtained. The value of V₃ is for the outer region of the solar system distance r₂. Therefore, the observed data are considered to be inaccurate, and no clear value is given at present.

Total mass and disk mass

The total mass M_t is obtained from equation (21) using the rotational velocity V₃ of the outermost r₃, which is the escape velocity from the galactic gravity. The M_t is obtained from equation (21) using the observed data, but as mentioned in Section 2, the new model also includes the hypothetical mass M_d2, which is the gravitational equivalent of the "new centripetal force". The specific explanation is covered in Section 4.1.

M_t = r_{3 ·V}²₃ /G = 4.2 × 10⁴¹ kg = 2.1 × 10¹¹ M.

(Mass of the sun M. = 2.0 × 10³⁰ Kg) = 27 M₀ (M₀ = 0.77 × 10¹⁰ M)

The total mass M_t of equation (21), obtained from the rotation curve V(r), is 27 times the bulge mass M₀ at the center of the galaxy. Most of the mass is the non-bulge mass, i.e., the disk mass M_d of the spiral. The disk mass  M_d (= M_t M₀) is then 26 M₀ (= 2.0 ×10¹¹ M. = 4.0 × 10⁴¹ kg). The estimates of the total mass M_t and the disk mass M_d , as well as the bulge mass M₀ , are agreed with the previous values at the order level.

These points are discussed in detail in Sections 4.1 and 4.3.

IAU recommended values for the solar system (R0, V0) = (8.5kpc, 220 km· S^–1)

In order to compare with the IAU recommended values, [5,21], which are the standard for measurement, one of the two parameters, the distance r or the V(r), is given in equation (20), and the other is obtained as the estimated value. Let V₂ and r₂ be the estimated values of the solar system, respectively, and the following values are obtained For R0 = 8.5kpc, the estimated value is V₂ = 218 km · S^–1. For V0 = 220 km · S^–1, the estimated value is r₂=8.9kpc. In both cases, the estimates agree well with the IAU recommendations within 5%.

Bulge end and rotational speed

Similarly, for the values of the bulge edge (r₀ and V₀), either one of the observed data can be given to estimate the other one. From the high accuracy of reading the data, the bulge end r₀ = 0.47kpc is obtained by givingV₀ = 285 km · S^–1_. The value of the bulge end r₀ read directly from the observed data is also obtained as r₀ =0.5kpc, which is in good agreement with the estimated value.

From the above, it is confirmed that the estimated value of V(r) (analytical solution) obtained from the new gravity model is almost consistent with the conventional physical quantity, even though the fitting was performed at a single point of the minimum data. From this, it can be inferred that the estimation accuracy of the analytical solution is quite high, and the new model is expected to be effective. Next, before verifying the rotation curve, the overall characteristics will be further estimated using the analytical solution V(r).

Prediction of the overall characteristics by analytical solution

Figure 6 shows the relationship between the distance r and the rotation curve (rotation speed) V(r) using the analytical solution of equation (20).

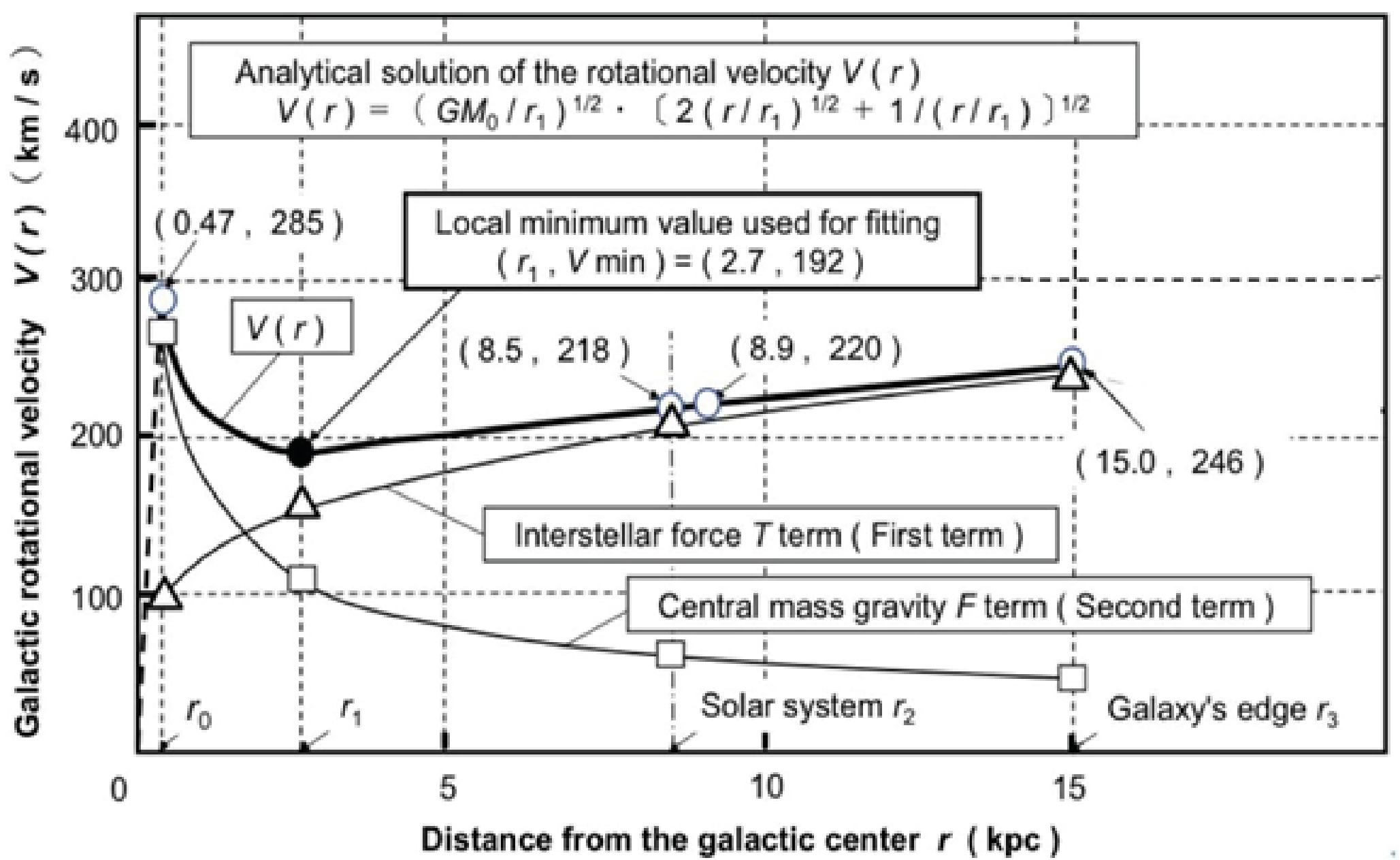
Figure 6: Characteristic curve of rotational speed V(r) obtained from analysis.

The graph of the analytical solution V(r) is shown by a thick solid line, representing the wide range from the bulge edge r₀ to the outermost galactic edge r₃. The local minimum (r_{1 ,} V_min) used for the fitting (observed data) is plotted as a black dot. Other characteristic points are the analytical values, plotted with various symbols. The first and second terms that construct the analytical solution V(r)  are separately represented by two thin solid lines, one for the interstellar force T term related to the disk mass M_d , and the other for the gravity F term related to the central mass (bulge mass) M₀. The analytical solution V(r) shows that the spiral galaxy is dominated by only two forces, and is composed of the bulge and the disk.

As can be seen from the functional form of V(r) with respect to the distance r, the first term rises abruptly, followed with a gradual linear increase. This feature is expected to correspond to the flattened rotation curve V(r), which has long been a mystery and could not be explained. The reason for the flattening was also predicted from the model described in Section 2. The gravity F(r)is inversely proportional to r², while the interstellar force T(r) is the function inversely proportional to r^1/2 from equation (8). As a result, the first term, the interstellar force T(r), is an increasing function proportional to r^1/4 without decreasing the rotation speed V(r) from equation (20). On the other hand, the second term is inversely proportional to the square root of the distance r and decreases according to Kepler's law.

Focusing on the outer region of the V(r) characteristics, the region from the distance r₁ of the minimum value to the outermost r₃ shows a characteristic line of increase. It can be seen that the rotation curve V(r) increases in the straight line with a gentle slope by adding the second term to the first term. The kinematic deduction for the meaning of this property is as follows: since the characteristics of V(r) shows the straight line with a gradual slope, it is inferred that the stars form the rigid body motion with the spiral shape. As a result, as discussed in Section 2, the group stars are considered to acquire the stable circular motion while maintaining a constant distance from each other.

Next, the physical quantities estimated in Section 3.2 are rechecked, taking into account the overall characteristics. First, using the peak value of V₀ = 285 km · s^–1 from the observed data, the bulge edge r₀ is 0.47 kpc. In contrast, if the neighborhood of the peak value is excluded, the maximum value of V_max is 246km · s^–1 at the outermost edge r₃. Even though the positional accuracy is low at this outermost end r₃= 15kpc, the estimation accuracy of  is estimated to be quite high because the V(r) characteristics increase with a gradual slope in the region from distance r₁ to outermost end r₃. The same is true for (R0, V0) = (8.5 kpc, 220 km· s^–1), which is the IAU recommended value for the solar system, and the estimation accuracy of V₂ = 218 km · s^–1  is estimated to be high.

Furthermore, at the outside positions (r > r₃) of the outermost r₃, the V(r)characteristics are only affected by the gravity of the total mass M_t (r₃)(=M₀ + M_d1(r₃)). Therefore, the V(r) characteristics are expected to decay according to Kepler's law.

Verification of analytical solution using observed data

In Sections 3.2 and 3.3, the values and the characteristics of V(r) were estimated using equation (20) of the analytical solution. In this section, the validity and accuracy of the model are verified in detail by comparing the analytical solution (the estimated characteristics) with the overall characteristics of the observed data.

The result of this verification is an important turning point in confirming whether the centripetal force T · cos θ of equation (3) used in the new model includes the new centripetal force (tentative mass M_d2) in the disk part.

Figure 7 shows the comparison between the analytical solution and the observed data for the characteristics of V(r) with respect to the distance r.

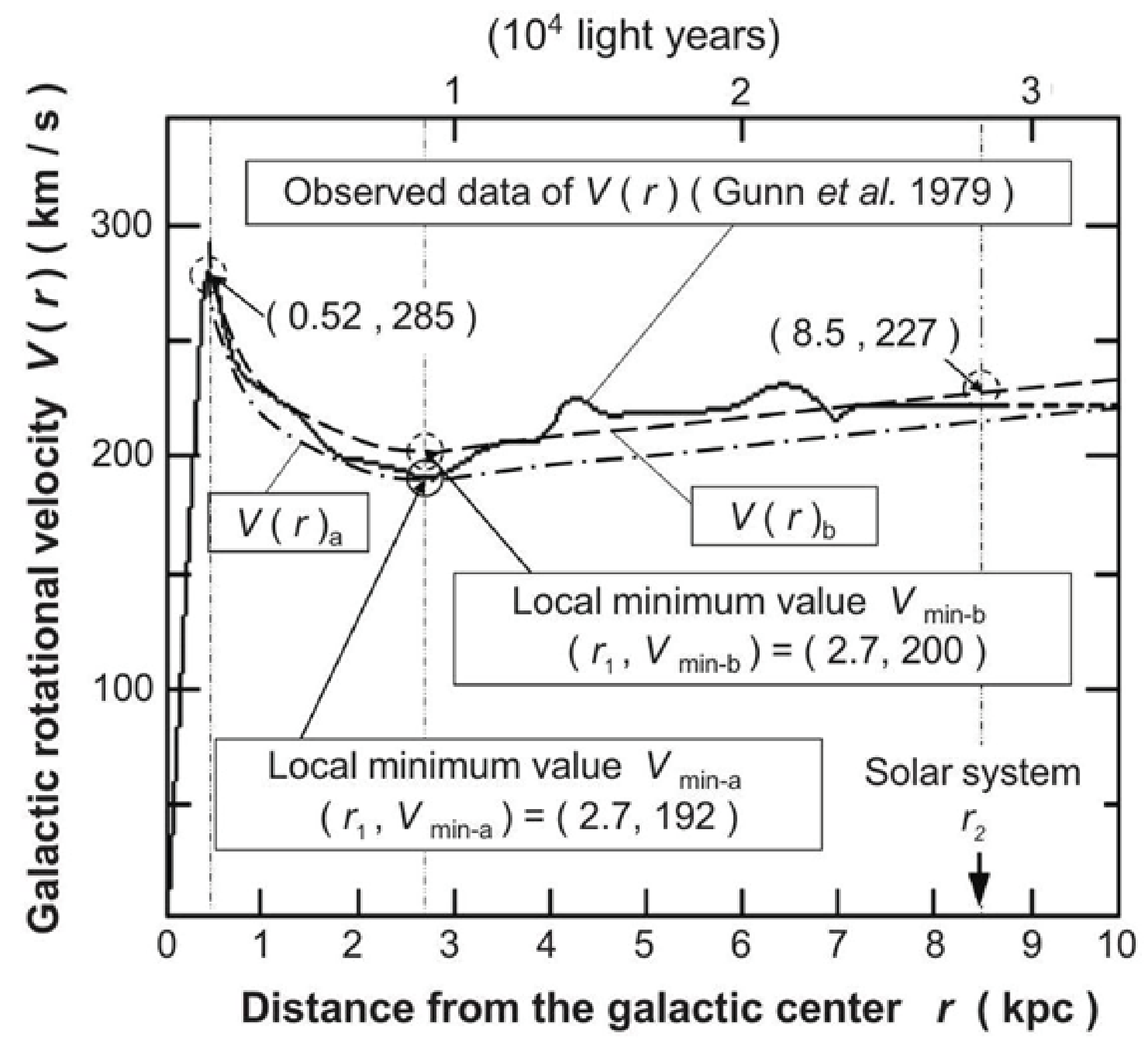
Figure 7: Comparison of the observation data and the analytical solution for V(r).

The observed data used here are those used in the fitting of the analytical solution V(r), and the overall characteristics including the same data are quoted [3]. The range of comparison for the characteristics is from the bulge edge r₀ to the solar system distance r₂ of the observational data. In other literatures, some data are measured up to the outermost r₃ of the galaxy, [8], showing the wide range of variation. The two axes in Figure 7 are set to match the scales of the observed data. The solid lines indicate the observed data, and the single-dotted and the dashed lines represent the cases of the analytical solutions V(r)_a and V(r)_b, respectively. The analytical solution V(r)_a is the case where the observed data V_min-a = 192 km·s^–1 is used for the minimum value fitting. The analytical solution  is the case where the new observation data V_min-b = 200 km · s^–1  is used as the minimum value. As in the analytical solution, the observed data show the steep peak value V_peak(=V₀) at the bulge edge r₀, the existence of the minimum value (r_1, V_min), and the linear and gradual increasing trend near the solar position r₂.

In addition, the V(r) characteristics show peculiar fluctuations of about 5% or so with respect to the central value, which is usually not seen in analytical solutions. This fluctuation is presumed to be caused by the effect of local spiral arms, but it is currently not separated from errors [14]. For this reason, the analytical solution V(r) is confirmed by direct comparison with the observed data. This fluctuation characteristics, along with the treatment of measurement error, will be discussed again in Section 4.4.3.

The characteristics of the analytical solution V(r)_a agrees with the observed data by a difference of about 10%, but is biased toward the lower end of the overall. This is because the minimum value (V_min-a = 192 km · s^–1), which includes the fluctuations, was set at the fitting process. As discussed in Section 2.1.2, the analytical solution of V(r) models the macroscopic relationship of the spiral shape. Therefore, for the verification, it is basically necessary to compare the characteristics at central values that are free of local fluctuations. The analytical solution V(r)_b shown by the dashed line takes this into account. The minimum value of V_min-b is about 5% larger than the minimum value of V_min-a, which is considered to eliminate the effect of fluctuations during fitting. As a result, the analytical solution V(r)_b is generally closer to the center value of the observed data (width of fluctuation characteristics) than V(r)_a, and agrees well with about ±5%.

Furthermore, if this fluctuation characteristics is not present, i.e., if it is not included in the measurement error, the characteristics of the analytical solution V_min-b are considered to be in almost agreement with the central value of the observed data.

In the following discussion, the V(r)_b is adopted as the analytical solution of the rotation curve in order to improve the prediction accuracy of the physical quantities. The value of the physical quantities associated with the change of the minimum value (from V_min-a to V_min-b) can be easily obtained by using the relevant analytical equation (relational equation). For example, the mass  is increased by 10%, giving the bulge mass M₀  as M₀ = 0.88× 10¹⁰M_,. Similarly, the disk mass M_d and the total mass M_t are also increased. In the case of the rotation curve V(r), it increases by 5% at the same rate with the V_min, giving V₃ = 258 km· s^–1. The modified physical quantities are discussed in Table 1 of Section 4.3.

From the above, it was confirmed that the analytical solution V(r) (=V(r)_b) derived by the new gravity model agrees for the full range of observed data with a difference of about ±5%, including the fluctuation characteristics. The flattening of the rotation curve, which has long been a mystery, has been successfully explained for the first time on the basis of Newtonian mechanics. This result basically confirms and verifies the correctness and reliability of the new model. Based on these results, in next Section 4, the interstellar force (centripetal force), the disk mass, and so on will be further analyzed and evaluated.

Analysis and Evaluation of Physical Quantities

In this Section 4, the physical corroboration for the various properties of the spiral galaxies will be presented. For this purpose, using the analytical solution as a tool, the characteristics of the spiral galaxies are widely analyzed to confirm the adaptability of the new gravity model and to derive the new knowledges.

Interstellar force and Disk mass

Existence of new centripetal force (Discovery of "macroscopic spiral effect")

The validity (correctness) of the analytical solution V(r) (equation (20)) derived from the basic equation has been verified by comparing it with the observed data. This result explains kinematically the flat rotation curve V(r) with the newly introduced interstellar force T(r).

The centripetal force T·cos θ of the disk part, described in Section 2.1.2, has been expected to include another new centripetal force in addition to the gravity by the real mass M_d1, to explain the complex V(r) characteristics. Both of these forces are given in unison as the centripetal force, which is balanced with the centrifugal force. However, the new centripetal force (hereinafter referred to as a "spiral force") works and acts in a completely different way from the gravity, as described in Section 2.

The relationship (reality) between these two forces is embodied in equation (22) by directly substituting the analytical solution V(r) of equation (20) for the centrifugal force in the basic equation (3).

V(r)²/r = (GM₀)/r ²+ (GM₀) · (2r₁^–3/2)/r^1/2 (22)

From the right-hand side of equation (22), the gravity of the bulge part and the centripetal force of the disk part are obtained, which are balanced with the centrifugal force. From this, the centripetal force T · cos θ is unified inversely proportional to r^1/2 owing to the addition of the macroscopic spiral force by the spiral motion to the gravity of the disk part. This can be also confirmed from equation (8) in Section 2.2. This property of the centripetal force T · cos θ indicates that the new spiral force in the disk part slows down the decay of the V(r) compared to the case of the gravity alone (inversely proportional to r²), which is the flattening factor of V(r).

This spiral force is caused by a macroscopic physical phenomenon that has never been considered before. Therefore, this phenomenon is hereafter referred to as a "macroscopic spiral effect. " I believe that the force caused by the spiral effect significantly changes the conventional concept of the centripetal force, and shows a new principle of the gravity generation for the spiral galaxies on the basis of Newtonian mechanics [11]. The principle is that "the new centripetal force (spiral force) is a force manifested by the interaction of Universal gravitation between the stars in the spiral motion (spiral effect), and the expansion of scale to the galactic system, and is formed in unison with the gravity". Here, the manifestation by the scale expansion is caused by the difference in the dependence for the distance  of the gravity and the spiral force.

The idea of this principle is still at the stage of being obtained from the analytical results, and it is necessary to confirm the conditions under which Universal gravitation is newly manifested (mechanism of its occurrence) by simulations, etc. The conventional Kepler's law is valid only when the centripetal force is the gravity but not for the galaxies with the spiral force.

From a different point of view, the generation of the spiral force is, in fact, the efficient generation of two centripetal forces by the star (real mass M_d1), including not only the gravity but also the spiral force by the form of the motion. As a result, the spiral force increases the V(r) characteristic linearly, approaching the rigid body motion that stabilizes the motion between the stars. The rigid body motion formed by this force is considered to be a necessary (selected) and intrinsic property as the means to obtain the stable circular motion.

From these analyses, the new model has a new principle of the gravity that significantly changes the conventional concept, and the following several findings (discoveries) have been newly obtained.

1. In the spiral galaxies, there exists a centripetal force that balances the centrifugal force, which is different from the conventional gravity.
2. Furthermore, in addition to the gravity generated by the real mass M_d1, there exists a new centripetal force (spiral force) by the grouped spiral motion (shape) in the centripetal force of the disk.
3. The two forces, the gravity and the spiral force of the disk, are generated in a unified centripetal force when the circular motion is combined with the spiral motion.
4. The flattening of the V(r) characteristics is not by the increase of the gravity (mass), but by the generation of a new centripetal force.

From the above, in finding a new concept of the centripetal force (new gravity principle), the cause (existence of the spiral force) of the flattening for the V(r) characteristics is clarified.

Properties of disk mass M_d (r) and total mass M_t (r)

In Section 4.1.1, it is mentioned that the spiral force is formed in the spiral galaxies separately from the gravity owing to the discovery of the new gravitational principle. However, there is a problem in dealing with them. That is, the two forces have different properties from each other, and are essentially united and inseparable. It is assumed that the problem of gravity (centripetal force) has long been unsolved in the spiral galaxies because of this complex nature (a new concept).

In the modeling of Section 2, the prediction for the existence of a new centripetal force (spiral force) has enabled this force to be equivalently converted into the gravity and discussed in terms of a mass. The disk mass M_d(r) has a hypothetical mass M_d2 ( spiral force) in addition to the real mass M_d1 ( gravity), and the two forces generated by different principles are equivalently replaced by a common gravity problem (two masses). As a result, it is possible to compare and evaluate with the conventional model (dark matter M_m). The remaining problem is to separate the two unified masses, which is currently not achieved. This leads to a practical problem, which will be discussed later.

First, the properties of the disk mass M_d(r)(=M_d1 + M_d2, r ≥ r₀), which is replaced by two masses, and the total mass M_t (r) will be discussed. The disk mass M_d(r) is given as 2(r/r₁)^3/2 times the bulge mass M0  shown in equation (23) by the gravity conversion. As described in Section 2, this converted mass is obtained by bracketing the centripetal force (second term) of the disk section shown in equation (22) with the gravity function G/r².

M_d (r)= 2(r/r₁)^3/2. M0 (23)

Equation (23) is expressed in a simple equation proportional to r^3/2 , but as mentioned above, it contains both the real mass M_d1 and the hypothetical mass M_d2 owing to the spiral force in one piece. The total mass M_t (r) is then given by equation (24).

M_t (r) = [2(r/r₁)^3/2 + 1] · M0 (24)

Using the analytical solution V(r) of equation (20), the new equation of the balancing relation shown in equation (25) can be derived for the total mass M_t (r).

V(r)²/r = GM_t (r) /r² (25)

By using the total mass M_t (r), it is shown that the centrifugal force f on the left-hand side is equal to the gravity F on the right-hand side, and the conventional basic equation (1) is satisfied. However, as mentioned above, the content is completely different because the M_t (r) includes the hypothetical mass M_d2 (spiral force) converted to the gravity equivalent.

In contrast, there is the problem that the disk mass M_d shown by equation (23) is estimated to be larger than the real (true) mass M_d1 owing to the addition of the hypothetical mass M_d2. Specifically, when the hypothetical mass M_d2 (spiral force) is dominant, the observed rotational velocity V(r) is large even when the true mass M_d1 is small. When the observed rotational velocity V(r) is abnormally large in small spiral galaxies, some reports have suggested the existence of a giant black hole (giant mass) in the center of the galaxy. In such cases, it is necessary to pay attention to the possibility that the increase of the rotational velocity V(r) is affected by the spiral force (mass M_d2).

However, these two masses M_d1 and M_d2 are not separable because they are unified in mass as in the case of the centripetal force. Therefore, the previous mass prediction is incorrect because the observed data V(r) includes the effect of the spiral force (the hypothetical mass M_d2).

Furthermore, since the conventional model introduces dark matter based on Kepler's law, it is unable to recognize that there is the problem (inaccuracy) in the prediction method itself. In order to solve this practical problem in the future, it is necessary to find the means to separate the hypothetical mass M_d2 of the spiral force.

Mass characteristics of the Milky Way

Looking at the disk mass M_d (r) in equation (23), the mass is already generated at the bulge edge boundary (r = r₀) where the spiral is generated, accounting for about 17% of the bulge mass M₀ . This is because, from the definition of the boundary condition shown in Figure 3, there exists the interstellar force T₀ /sin θ that generates the spiral shape (spiral arms) at the bulge edge r₀. From this definition, there exist T₀ and T₀ /cot θ as the tangential and vertical components of the interstellar force T, respectively. These interstellar components are considered to be caused by the formation and connection of the new centripetal force (the hypothetical mass M_d2 of the spiral force) described in Section 4.1.1, at the boundary r₀.

In the interior of the bulge, in addition to the formation of the mass M_b(= M₀) by the central core and the black hole (the bulge structure: a rigid sphere), it is assumed that the structure that is the source of the interstellar force T (centripetal force) is formed simultaneously. From the above, the disk mass M_d (r) is considered to be equivalently formed also inside the bulge (0 ≤ r ≤ r₀) from the continuity of the spiral force.

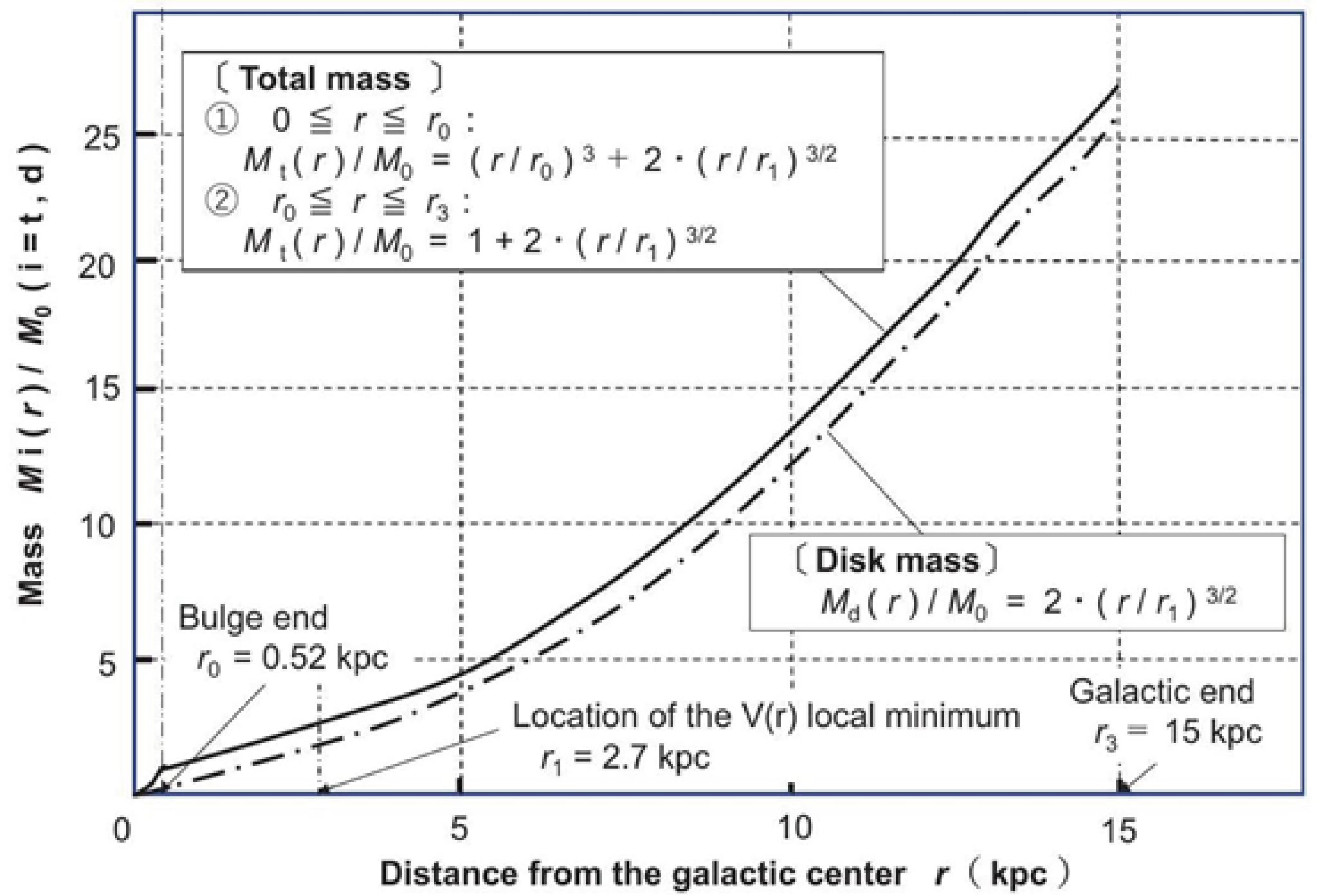
Figure 8: Predicted distribution of M_d (r) and M_t (r) in the Milky Way

Considering the above, the predicted distribution for the disk mass M_d (r) and the total mass M_t (r) with respect to the distance r is expected to be as shown in Figure 8.

So far, when dealing with the region of motion, the distance  from the galactic center has been considered inside the spiral arms along the spiral geometry (at the center position). If the case where the distance r is taken in the radial direction and crosses the spiral arms is considered here, there is a two-dimensional space in which the spiral force (hypothetical mass M_d2 (r) is structurally not generated. However, as mentioned in section 2.1.2, in the external space without the spiral arms, the stars are in an unstable state of motion and are absorbed by the neighboring spiral arms (mainly the inner arms) and cannot exist (do not exist) in a steady state.

The distribution of the disk mass M_d(r) shown by the single-dotted line in figure 8 follows equation (23). In the previous discussion, the distribution within the bulge region (0 ≤ r ≤ r₀) is considered to be continuous through the boundary r₀. The total mass M_t (r) in the disk region (r₀ ≤ r ≤ r₃) takes the form of the distribution in equation (23) plus the mass M₀ of the bulge, as shown by the solid line.

From the distribution in Figure 8, the mass M_d(r) in the disk region (r₀ ≤ r ≤ r₃) is indicated by a single dotted line and increases monotonically in proportion to r ^3/2. In the conventional paper, ¹⁴⁾ the rotational velocity V(r) is considered to be nearly constant based on the observations and equation (1), and the mass is assumed to be proportional to the distance r. Therefore, the rate of increase of the mass is much smaller than r ^3/2 of the new model. This difference is caused by the difference in the presence or absence of the spiral force found in the new model. This is because the V(r) characteristics obtained in the observed data are not exactly flat, but rather increase with the gradual straight line as shown in equation (20). If the V(r) characteristics are kept constant, the spiral shape collapses by the rotational motion without the rigid body motion, which is inconsistent.

In addition, for the total mass M_t (r) shown by this solid line, the rate of increase of the mass decreases rapidly at the bulge end r₀. This is explained by the spike-like peak value (V₀) at the bulge edge r₀ shown in the characteristics of the rotation velocity V(r) in Figures 6 and 7. In contrast, the total mass M_t (r) within the bulge region (0 ≤ r ≤ r₀) is newly predicted as in equation (26).

M_t (r) = (r/r₀)³ . M₀ + 2 . (r/r₁)^3/2 . M0 (26)

The first term is the mass distribution M_b (r) estimated from the rigid structure of the bulge. From the data in Figure 7, the bulge is considered to be the rigid sphere with the constant density. The second term is the disk mass M_d (r) inside the bulge, which is occupied by the hypothetical mass M_d2 involved in the formation of the spiral force, and assumes the continuity with equation (23). The connection structure with the spiral arms may be affected by the interior of the bulge, and the second term should be treated as a single model and verified separately.

Existence of Local Minimum

Physical quantity related to the minimum value

In the process of deriving the rotation curve V(r) (analytical solution) from the basic equation (3), the existence of local minima (r₁,V_min) was focused on. The existence of this minimum had already been confirmed by the observational data of the Milky Way, but its importance had not been clarified. In this study, the existence of the minimum has been predicted and confirmed kinetically for the first time from the functional form of the distance r shown in equation (11). As a result of the analysis in Section 3, two relations for the minimum (r₁,V_min) are obtained and found to have the new meaning.

That is, most of the relational equations involving the rotation curve V(r) can be directly related by the parameters of the minimum (r₁,V_min).

From the following equations, it is inferred that the minimum is the important parameter governing the formation and motion of the spiral galaxies.

1. The bulge mass M₀ shown in equation (16) is described only by the values of the parameters r₁ and V_min. This equation is a new finding obtained kinetically by the minimum value analysis.
2. The rotation curve V(r) shown in equation (20) is described by the minimum parameters r₁ and V_min for all coefficients. This is also the case.
3. The disk mass M_d (r) and the total mass M_t (r) are described by the parameters r₁ and V_min, where all coefficients are the minimum value, as shown in equations (23) and (24)
4. Furthermore, by transforming equation (16), the equation of motion with the balancing condition shown in equation (19) can be obtained.

As mentioned above, it is shown that the centrifugal force f (r₁) is balanced by three times the bulge gravity F (r₁) at the minimum value (r₁, V_min). From another viewpoint, the centripetal force T · cos θ generated by the disk is equal to twice the bulge gravity F (r₁). These relations, which are also obtained from the rotation curve V(r) in equation (20), make a kinematic sense.

In contrast, the relation in equation (16) is an analytical expression, and thus the characteristics of the spiral galaxies can be estimated newly. For example, let consider the case where the bulge mass M₀ is kept constant and only the minimum value (r₁, V_min) is varied, using equation (16).

This corresponds to the case where the spiral shape changes, etc., which means that the interstellar force T(r) changes. When the position r₁ of the minimum increases, the velocity  V_min decreases and the effect of T(r) decreases. In other words, Kepler's law is approached.

Conversely, when the position r₁ decreases, the velocity V_min increases and the influence of T(r) increases. The ultimate state of the galaxy can be estimated to approach the case where the former has no spiral arms (i.e., it is not a spiral galaxy), and the latter has only spiral arms (i.e., the bulge mass  is negligible). The case of the spiral galaxies with no or negligible bulge mass M₀ will be discussed separately in Section 4.4.1 below.

Thus, the existence of the minimum (r₁, V_min) gives a kinematically important relation to the characteristics of the spiral galaxies.

New disk region delimited by minimum value

In the disk region (r₀ ≤ r ≤ r₃), the state of force balance changes before and after the distance r₁ as described in the V(r) characteristics in Figure 6. As a result, two new regions exist: an unstable inner region (r₀ ≤ r ≤ r₁) and a stable outer region (r₁ ≤ r ≤ r₃), as shown below.

In the outer region of the disk (r₁ ≤ r ≤ r₃), the spiral arms of the stellar population exhibit the rigid body motion in which the V(r) characteristics increase linearly for the distance r. Although this is different from the original rigid body rotation with the galactic center as a fixed point, the circular motion of the star and the spiral motion of the stellar population are geometrically rotating toward the same direction and with the same angular velocity, and thus are considered to be in the rigid body motion. As described in Section 3.3, the stars in this region have a stable rotational motion maintaining their mutual positions (distances) and the spiral shapes by the rigid body motion. On the other hand, for the inner region (r₀ ≤ r ≤ r₁), the V(r) characteristics show different changes from the rigid body motion. However, as seen in the literature [19], showing the spiral shape, the inner region does not show the clear observational data describing the spiral behavior. In this region, the centripetal force T · cos θ is small, so the three-dimensional motion by the gravity F (r) is intensified, and the V(r) characteristics approach Kepler's law. The inner region is sandwiched between the rigidly moving outer region and the bulge, and it is inferred that chaotic states are mixed and formed by the structural switching of the motion. Although the spherical bulge is said to exhibit the rigid body motion in the V(r) characteristics, the mechanism of the formation of its ultimate long stable state has not been fully elucidated. One hypothesis is inferred that the inner region is the transitional region where the rigid motion is converted from the two-dimensional structure (outer region) to the more stable threedimensional structure (bulge). This is assumed to be related also to the evolutionary process of the spiral galaxies. The rigid body motion in the outer region has been found to be caused by the existence of the spiral force, which is a new concept based on the previous analysis. Similarly, for the bulge, which is considered to be the rigid sphere, the force based on a new concept is considered to dominate the three-dimensional rigid body motion. Therefore, in order to elucidate the formation mechanism of bulges (and elliptical galaxies), it is important to observe and investigate the kinematic state of the inner region for which there have not been sufficient observational data , from the viewpoint of the rigid body motion.

From the above, the minimum value (r₁, V_min) in the disk region that makes the characteristic inner region be recognized, will be an important guideline for understanding the formation mechanism of the spiral galaxies in terms of kinematics.

Physical quantities used in new model

The verification by the analytical solution of the rotation curve V(r) has given many insights, new relations, and physical quantities. In particular, the existence of a new centripetal force (spiral force) generated by the spiral effect not only solved the mystery of the V(r) characteristics but also led to the discovery of a new principle of the gravity generation. Table 1 shows the main physical quantities treated in the new model. The structure of the spiral galaxies is derived from the rotation curve V(r) of the analytical solution, and consists of two regions: the bulge and the disk. This is different from the conventional classification of three regions including the dark halo (dark matter).

Furthermore, the area of motion of the disk section is also limited to the interior of the spiral arms, which is very different from the concept of the conventional model.

Table 1 shows the observed data (~ r symbols) used in the analysis and the Miyamoto and Nagai model (MN model) values (M_b = M₁, M_d = M₂) used in the mass comparison [15]. Based on the validation results in Section 3.4, the analytical solution V(r)_b with the minimum value of V_min-b = 200 km is adopted, and the related physical quantities are shown in Table 1.

Bulge region (0 ≤ r ≤ r₀)

The value of radius  is obtained by back-calculating from the analytical solution V(r)_b using the observed data of 285 km · s^–1_. This value is consistent with the r₀ value obtained from the observations.

The mass M_b is obtained kinematically for the first time from equation (16), which gives the analytical solution , unlike the conventional method. Compared with the mass M₁ (corresponding to the mass M₀ ) in the MN model (assuming no dark matter and only the galactic plane balance condition), this  is about half of the M₁.

Disk region (r₀ ≤ r ≤ r₃)

In Section 2, the aperture ratio α, the pitch ∆ф, and the (spiral) exponent α are newly used in the modeling of the spiral geometry. These parameters determine the coefficients of the interstellar force T(r), which is a macroscopic force.

Table 1: Physical Quantities (Property Values) used in New Model

By deriving the V(r)from the T(r), the fitting has been performed with a single minimum value (r₁, V_min) of the observational data. As mentioned in Section 4.2, this minimum (r₁, V_min) is the parameter that governs and controls the motion of spiral galaxies, and is related to most of the physical quantities obtained by the analytical solutions shown in Table 1. Furthermore, the disk region is divided into two main regions: an unstable inner region (r₀ ≤ r ≤ r₁) and a stable outer region (r₁ ≤ r ≤ r₃), where the b princip alance of the centripetal forces changes around the distance r₁.

The disk mass M_d (= M_d (r₃)) includes a hypothetical gravitational mass M_d2 corresponding to the spiral force in addition to the real mass M_d1, by the discovery of a new concept in the gravity principle; as mentioned in Section 2, the mass M_d2 is introduced to compare the spiral force with the gravity, and does not involve real physical phenomena. These two masses M_d1 and M_d2 generate simultaneously in union as the essential property of the spiral galaxies, as described in Section 4.1.

Therefore, the real mass M_d1 of the disk section requires the removal of the hypothetical mass M_d2from the disk mass M_d (r₃). However, the hypothetical mass M_d2 cannot currently be separated and is shown in Table 1 as the united disk mass M_d (r₃). The separation of this mass M_d2 is an important issue for the future.

In contrast, the conventional model can not recognize the above issue (problem) because the flattening of V(r) is considered to occur by a new increase in the gravity. Table 1 shows that the disk mass M_d (r₃), including the hypothetical mass M_d2, is only about 15% smaller than the mass of the MNmodel (M₂). As with the bulge mass M_b, the value is smaller. The rotational velocity V (r₂) of the solar system at r₂ =8.5 kpc is 229 km· s^–1  using the V(r)_b. This agrees with the IAU recommendation (R0, V0) = (8.5kpc, 220 km· s^–1), within 3%, and both values are estimated to be extremely accurate. The outermost velocity V (r₃) is similarly obtained to be 258 km · s^–1 using V(r)_b. Currently, there is no accurate observation data available for the comparison, but the small velocity change around the distance r₃ suggests that the accuracy of the estimation is quite high (within 3%) as well.

Whole region (0 ≤ r ≤ r₃)

The mass M_t (= M_t (r₃) =M₀ + M_d (r₃) ) of the whole region can be obtained from the analytical solution using V_min-b by equation (24). Comparing this value with the mass of the MN model, the overall mass is about 80%, since the mass is reduced in both the bulge and disk regions. In this comparison, as mentioned earlier, the disk mass M_d (r₃), which includes the converted mass, is used, and the real mass (M₀ + M_d1) is even smaller. In contrast, when the overall characteristics of the rotation curves are compared for r = 10kpc and above, there is a large difference in their variation [15]. In the MN model, the V(r) characteristics tends to decrease in the outer region, suggesting that the dark halo (dark matter) is necessary to flatten the V(r) characteristics [14]. Conversely, the new model shows the flat property even for the small masses. As discussed in Section 4.1, the flattening characteristics are caused by the new centripetal force, which is largely affected by the spiral effect (spiral force).

Characteristics of spiral galaxies

Quarter power law of rotation curve V(r)

The new features of the spiral galaxies can also be obtained by examining two terms in the analytical solution V(r). In the case of the Milky Way, the first and second terms of equation (20) yield the minimum value of the characteristics. As described in section 4.2, for the spiral galaxies, it is possible that the second term does not exist from the relation in equation (20), i.e., the bulge mass M₀ is absent or can be neglected. In such the case, the V(r) characteristics are only the first term which is related to the interstellar force T(r). As a result, the new property that the V(r) is proportional to the  power of the distance r (predicting the existence of the " 1/4 power law") can be easily derived.

However, if the bulge mass M₀ does not exist, the new relation (the condition for giving another coefficient) is needed instead of the coefficient M₀ used for the V(r) characteristics and the disk mass M_d (r) in the analytical solution. This condition can be given for the outermost r₃ instead of r₁ where the minimum exists. Since the sum of the disk mass M_d (r₃) and the bulge mass M₀ is equal to the whole mass M_t (r₃), this can be used to relate to the escape velocity V_max at the outermost end r₃. Therefore, the result is basically the same as the one-point fitting case. Using the fact that the disk mass M_d (r) is proportional to r^2/3 from equation (23), the following equation (27) can be derived

M_d (r) = (r₃ ^–1/2· V_max ²/G) · r^{3/2 (27)}

Equations (23) and (27) for the disk mass M_d (r) give the same relationship, although the coefficients are different depending on the presence or absence of the bulge mass M₀. Furthermore, using equation (20), the 1/4 power law of equation (28) is derived from the balancing condition.

V(r) = V_max · (r/r₃)^{1/4 (28)}

From this, when the bulge mass M₀ can be neglected, the analytical solution for the disk mass M_d (r) and the rotation curve V(r) is basically obtained. Therefore, as seen in the first term of the V(r) characteristics shown in figure 6 , if the V(r) can be determined to be proportional to r^1/4, it can be inferred that the spiral galaxy of interest has no bulge mass M₀, or can be ignored.

Next, in order to confirm the existence of the 1/4 power law, the validity of the law is compared and verified using the observed data. Focusing on the observed data of the V(r) characteristics, the data related to the 1/4 power law can be found in the paper (9) by Rubin et al. In this paper, they examine the properties of 21 Sc galaxies and discuss the relationship between the outermost distance R_f (= r₃) and the maximum velocity V_max (= V(r₃)).

These two parameters are related to equation (28), but the 1/4 power law is not specifically discussed. This is presumably because the analytical solution of equation (28) had not yet been obtained. Figure 9 shows the relationship between the distance r and the rotation curve V(r) using the mean data of 21 Sc galaxies.

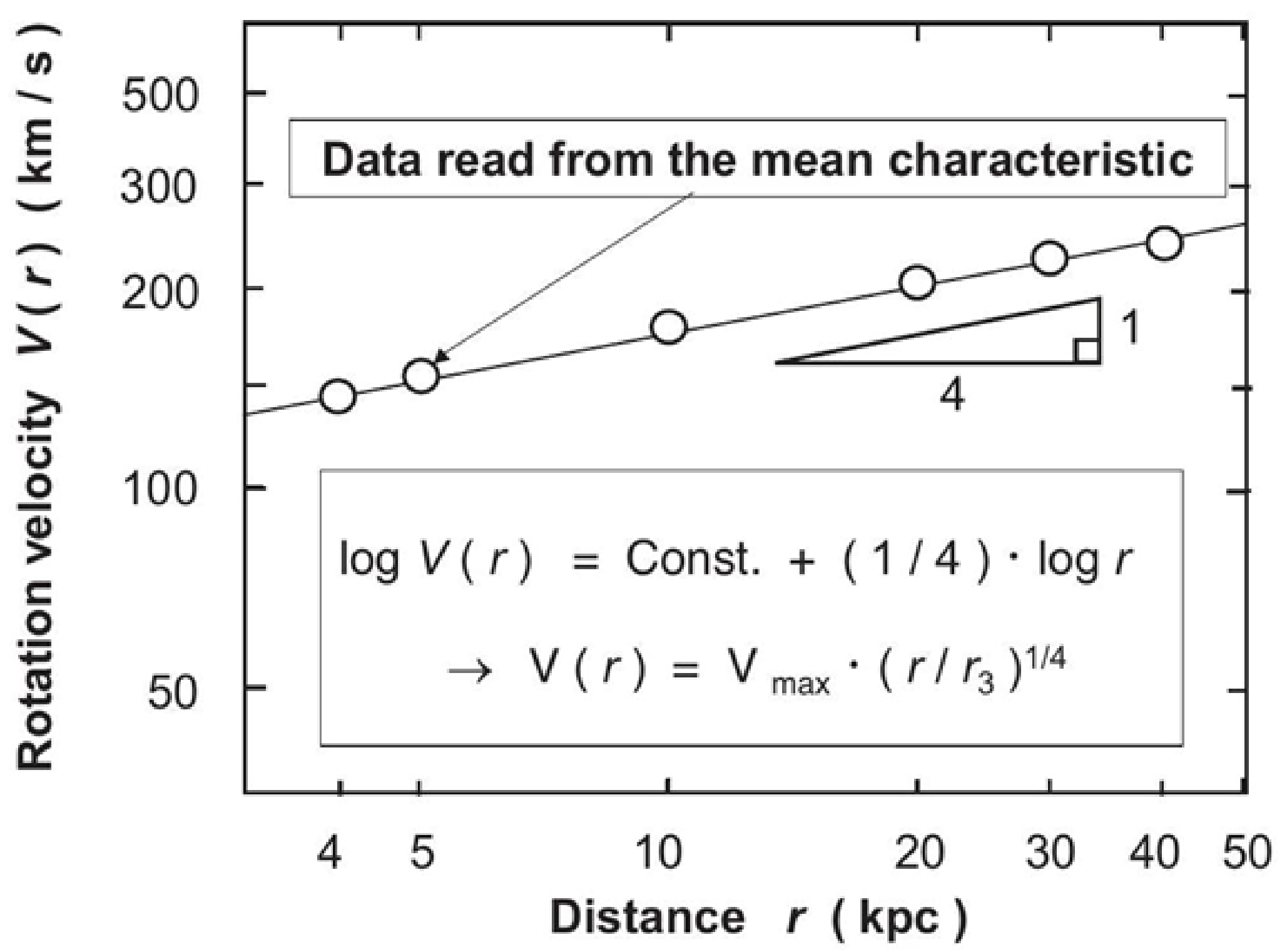
Figure 9: Relationship between distance  and rotation velocity V(r) for 21 Sc galaxies. The graph is obtained by reading 6 data points from the mean value characteristics of 21 Sc galaxies obtained in the reference [9], and plotting the rotation velocity V(r) again. the both logarithmic graph shows a straight line with the slope 1/4, which confirms the existence of the 1/4 power law for the distance r.

In Figure 9, the values read from the averaged data are plotted in both logarithms as a straight line, indicating that the rotation speed V(r) is proportional to r^1/4. This result confirms the existence of the 1/4 power law in equation (28). From this, it is inferred that the Sc galaxies, which are considered to be many small galaxies, have no or negligible bulge mass M₀. In the observed data of the Sc galaxies, there are various patterns in the rising state of the V(r) characteristics while the 1/4 power law holds [9]. The reason is probably the difference in the magnitude of the bulge mass M₀.

As mentioned as the hypothesis in Section 4.2.2, the spiral galaxies are considered to be in the process of formation (evolution) to the rigid body motion. In the early stage of the galaxy formation, it is considered that there were many spiral galaxies with no or negligible bulges (the case of Sc galaxies). In the later stages, the spiral shape is considered to have expanded and formed the bulge (rigid sphere) in its center (the case of the Milky Way). Finally, the galaxy is considered to have evolved into the more stable galaxy (elliptical galaxy), shown in the Hubble Shape Classification. Therefore, the result of the verification for the quarter power law without the bulge is important for the early formation of spiral galaxies (the direction of the galaxy's evolution).

Maintenance function and characteristic value of spiral exponent

The exponent α is given as the function of the spiral shape parameters, the pitch ∆ф and the aperture ratio α, from equation (9), and is obtained from the observed data [19].

As described in Section 2.3, the pairs of point-symmetric spiral arms exhibit the different values for the pitch ∆ф and the aperture ratio α, respectively, but the characteristics of the galaxy as a whole maintain the stable spiral motion. This is presumably by the fact that the spiral galaxies have the property of maintaining the spiral shape while satisfying the force balance condition. In order to verify this point, the relation between the pitch ∆ф and the aperture ratio α with respect to the exponent |α| is shown in Figure 10.

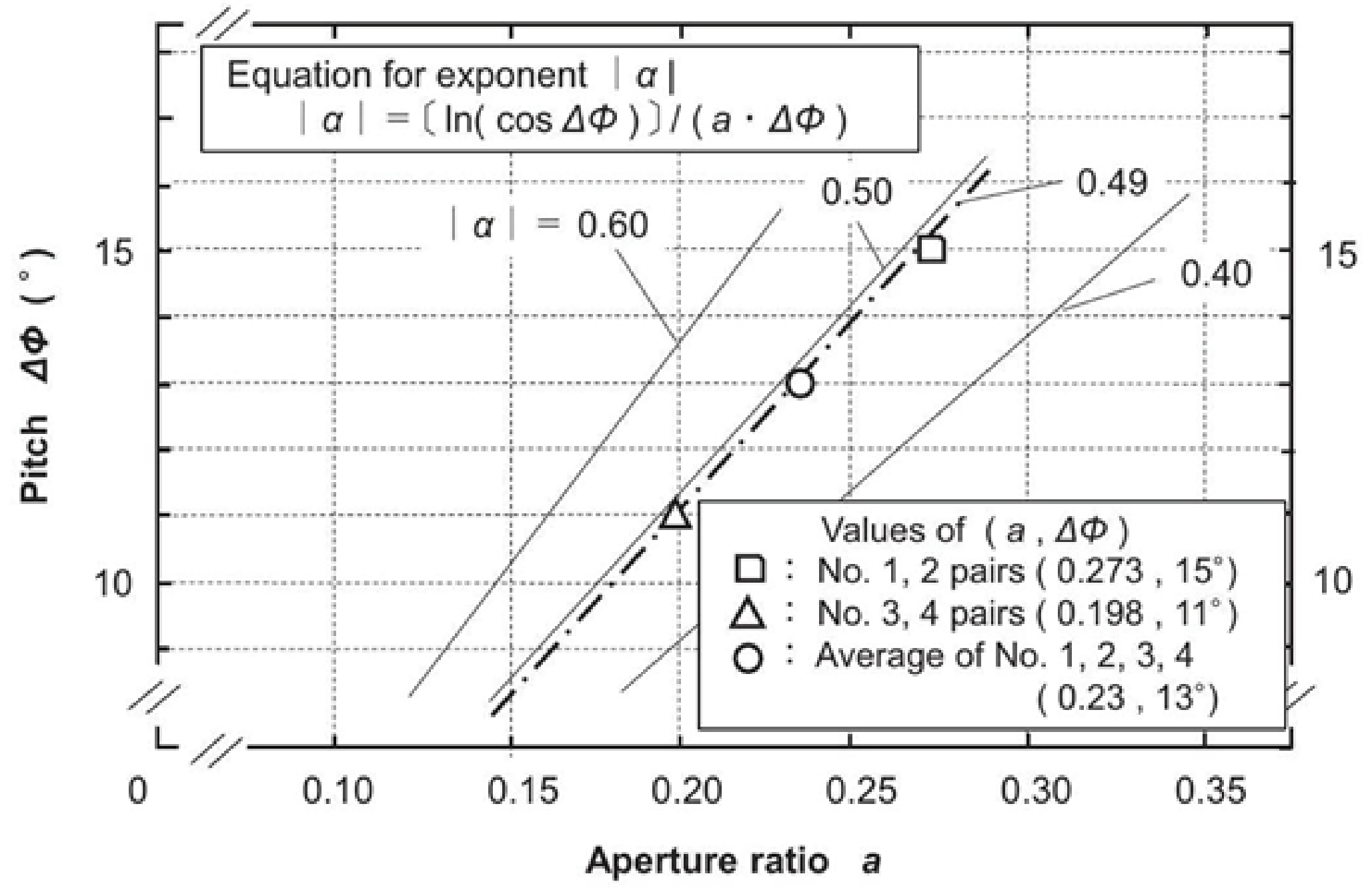
Figure 10: Aperture ratio α and pitch ∆ф of the Milky Way ( for constant spiral exponent |α|)

Figure 10 shows that the relationship between the aperture ratio  and the pitch ∆ф is linearly proportional when the exponent |α| is constant. The circular mark indicates the case where the aperture ratio α and the pitch ∆ф are set to 0.235 and 13^⁰ as the average values of the observed data, respectively. The exponent |α| in this case is 0.49 (set to approximately 0.5 in Section 2.3). Plotting the data for each spiral arm with the square and triangle marks, respectively, shows that both of them lie on the straight line (single point line) with the exponent |α| = 0.49 as well as the circle mark of the mean value. This indicates that the value of the exponent |α| maintains the complex shape of the spiral galaxy stably by the balancing condition that keeps the exponent constant.

From the above, it is inferred that the spiral shape (spiral arms) has the function that keeps the exponent |α| constant (0.5) even when the aperture ratio α and the pitch ∆ф are changed.

Next, let consider the meaning of the value (0.5) taken by the exponent|α|. The value of the exponent |α| may be a universal property of the spiral galaxies, including the Milky Way, based on the existence of the 1/4 power law found in Section 4.4.1.

So far, from the observational data of the spiral shapes, the exponent |α| that determines the T(r), i.e., the V(r), has been found to be 0.5. The result of the previous analysis shows that the value of this exponent |α| has the function of keeping the value constant even when the spiral shape (the parameters α and ∆ф) is changed. Considering the stability of the spiral galaxies, it is inferred that the value is the special value that is universally applicable not only to the Milky Way but also to the other galaxies. In other words, the value of 0.5 for the exponent |α|, which is obtained from equation (9), may be an inevitable value for the spiral galaxies.

To confirm this, next let to examine the exponent |α| analytically. The exponent |α| is analytically related to the T(r) in equation (8) and to the T(r) in equation (20). Removing the bulge mass M₀ term from the V(r) the T(r) term remains, and it is proportional to r^1/4. This can occur analytically only when the exponent |α| is 0.5.

Therefore, if the data from other galaxies directly confirm that the rotation curve V(r) is proportional to r^1/4, the value of 0.5 is no longer a coincidence value. As discussed in Section 4.4.1, the 1/4 power law applies in the absence of the bulge mass M₀, and is verified by the characteristics of the Sc galaxy shown in Figure 9 above. This result indicates that the exponent |α| takes the value of 0.5 for many Sc galaxies.

Since the value of the exponent |α| obtained for the Milky Way is also valid for the Sc galaxies, it is assumed to be a characteristic value that indicates the universal value for the spiral galaxies. From the above, the spiral galaxies including the Milky Way are inferred to have the function to maintain the characteristic value of the exponent |α| (0.5) for the spiral shape ( the parameters α and ∆ф).

Fluctuation Characteristics of Rotation Curves

Most observed data of V(r) characteristics show large fluctuations in the flat region, and two views have existed so far [14]. One, currently considered the mainstream, says that the fluctuations are errors caused by measurement errors and projection uncertainties, and are said to be less than ±8 km· s^–1. For this reason, most V(r) characteristics are corrected by the averages and not shown by individual measurements.

The other is found especially in the paper by Vera Rubin et al. which claims that fluctuations are not errors but correct measurements. In the paper (1978) [14], two types of observed data are shown, Figure 2 (individual measurements) and Figure 4 (averaged values). They point out that the fluctuations are secondary depending on the position (distance) inside the spiral arms (20 km · s^–1 lower at the inner edge of the spiral arms than at the outer edge) and are pronounced in NGC 2998 of the Sc galaxy. However, despite the large velocity fluctuation range, the cause of this problem has not been shown. Since that time, the flattening of the V(r) characteristics has been a major problem (not obeying Kepler's law), and it is assumed that this was due to the fact that this problem had not yet been solved.

The data for V(r) characteristics discussed in the validation of Section 3 show large fluctuations, inferring that they mainly reflect the results of individual measurements.

Considering the flattening problem solved once again this time, the analytical solution V(r)_b of the new model is basically located at the center value of the observed data and is in close agreement, as shown in Figure 7 in Section 3.4. Therefore, the fluctuations (secondary velocity fluctuations) generated in the spiral arms are assumed to be inherent characteristics rather than errors in the measurement.

Based on this, the following new fluctuation model is proposed, focusing on the cross-sectional structure of the spiral arms. Grouped stars in rigid motion are affected by a local gravity toward the center in the cross-sectional structure of the spiral arms. This gravity is additive to the macroscopic centripetal force (T · cos θ), but acts in opposite directions at the inner/outer edges of the spiral arms, generating a positive velocity gradient in the V(r) characteristics. At this time, the velocity gradient in the data (Figure. 2) [14], tends to relax near the two ends (inner/outer edges) in the spiral arms, suggesting that a secondary gravity drop is occurring as one moves away from the center.

In the future, when the V(r) data is handled, the fluctuations are inherent characteristics (secondary velocity fluctuations) and need to be evaluated separately from the measurement error. Analyzing velocity fluctuations by focusing on the crosssectional structure will improve the measurement error evaluation and may reveal new insights into the disk section including the spiral arms.

Conclusion

The purpose of this study is to elucidate the flattening of the rotation curve V(r) for the spiral galaxies including the Milky Way, which has been a long-standing mystery (not following Kepler's law). For this purpose, a new gravity model based on Newtonian mechanics was proposed and successfully verified it for the first time.

Furthermore, in order to corroborate the verification results, the characteristics of the spiral galaxies were extensively analyzed using the analytical solution as a tool. In the process, the physical phenomenon (macroscopic spiral effect) that had not been considered before was discovered, and a new principle of gravity generation (gravity theory) was found, as well as many important findings.

I hope that the new model will be used as a useful tool to deepen our understanding of the spiral galaxies in the universe in the future.

Proposal and validation of new gravity model

The model is characterized by the fact that it focuses on the rigid body motion (spiral motion) indicated by the shape of spiral galaxies and predicts the existence of a new force "interstellar force T(r)" along the shape of the spiral arms (in the tangential direction). This force T(r) is generated by the macroscopic interaction of Universal gravitation between the grouped stars and can be vectorially divided into two components: a centripetal force that increases the centrifugal force and a force that maintains the spiral shape.

The model proposes a new basic equation in which the centripetal force plus the conventional gravity balance the centrifugal force. Based on the basic equation, an analytical solution V(r) of the rotation curve is obtained, which is compared with the observed data and verified. As a result, the V(r) characteristics are in agreement for the first time for the whole region from the bulge edge to the solar system with a difference of about ±5%, including the fluctuation characteristics.

This confirms the validity and correctness of the new model, and at the same time, it is found that the flat characteristics of V(r) are caused by the existence of a new interstellar force T(r).

Complex physical phenomena of interstellar force

The difficulty of elucidating the reality, which has been a mystery for more than 90 years, lies in the existence of a new concept (complex physical phenomena with the macroscopic interstellar force T(r)) that cannot be considered in the conventional theory of gravity. In order to theoretically support this, the following analysis is performed based on the results of the verification. The centripetal force T · cos θ by the interstellar force T(r) generates a new force called "spiral force" in addition to the gravity, which is associated with the spiral motion of the real disk mass M_d1. This spiral force is united with the conventional gravity and takes the form proportional to r ^–1/2. The centripetal force T · cos θ decays more slowly (r ^–1/2) than the case of gravity alone (r^–2) by the addition of the spiral force, and becomes the flattening factor of V(r). From this, it is found that the real mass M_d1 of the disk part, accompanied with the spiral motion in the circular motion, generates two forces (gravity and spiral force) simultaneously and in unison, which are balanced with the centrifugal force. This is a new physical phenomenon, which is considered to be the "macroscopic spiral effect".

New generation principle of gravity (new theory of gravity)

The generation of a new centripetal force (spiral force) significantly changes the conventional concept of gravity (centripetal force). On the basis of Newtonian mechanics, I believe that this represents a new principle for the generation of gravity.

This spiral force is manifested by the interaction between stars in the spiral motion (interstellar force T(r)) and the expansion of the scale to the galactic system, and is formed in unison with the conventional gravity. The reason for this unification is that the real mass M_d1 of stars involves the source of the two forces, the presence of mass and the spiral motion, simultaneously. The reason it appears at the extended scale is that the gravity and the spiral force each have a different dependence for the distance r.

From this, it is inferred that the spiral galaxies have the essential property that the spiral force, which makes the spiral shape (motion) rigid, stabilizes the circular motion of the grouping stars by maintaining the interstellar distance r” constant. This principle is still at the stage of being obtained from the analytical results, and it is necessary to confirm the relationship between the mechanism of the spiral force generation and the rigid body motion by the simulations, etc. in order to obtain the conditions for applying the gravity model.

Intrinsic issue of spiral force

There is an intrinsic issue with the existence of the spiral force owing to its nature.

That is, the spiral force is a new centripetal force united with the gravity, and the two forces cannot be evaluated separately at the present time. This is an important issue in predicting the real mass. The disk mass M_d(r) (equation (23)) is expressed as the sum (M_d1 + M_d2) of the real mass M_d1, which generates the gravity, and the hypothetical mass M_d2, which is the equivalent mass of the spiral force converted to the gravity. These two masses M_d1 and M_d2 cannot be separated because they are united in the converted mass as in the case of the spiral force. As a result, the real mass M_d1 cannot be obtained independently, and the disk mass M_d(r)  is estimated to be larger than it actually is. In the conventional mass estimation, the observed data V(r) includes the effect of the spiral force (hypothetical mass M_d2), and thus needs to be corrected.

However, since the conventional model is based on the assumption of Kepler's law, the prediction method itself cannot be recognized as the problem. In order to solve this prediction problem(issue), it is necessary to find the method to separate the hypothetical mass M_d2 from the disk mass M_d2(r).

Characteristics and physical quantities of spiral galaxies

From the analytical solution V(r), the spiral galaxies are found for the first time to be composed of two regions, the bulge and the disk. As a result, there is no need for dark matter (dark halo) and the view of spiral galaxies in the universe changes dramatically. Furthermore, as mentioned in Section 2, the region of motion targeted by V(r) is the interior of the spiral arms that generate the interstellar force T(r), which is a major difference from the conventional model. In the new model, a stable state of motion cannot be maintained outside of the spiral arms, which basically cannot exist.

The estimates of various physical quantities for the Milky Way are quantitatively obtained from the analytical solutions V(r)_b, etc., as shown in Table 1. Among them, the disk mass M_d(r) includes the hypothetical mass M_d2 from the unified problem discussed in Section 5.4 above, and does not indicate the real mass M_d1 (true mass) at present.

In contrast, the bulge mass M₀, which is unrelated to the unification problem, is obtained for the first time kinetically by the analytic solution of equation (16). The estimated rotational velocities V (r₂) = 229 km · s^–1 and V (r₃) = 258 km · s^–1 are expected to be as accurate as the verified results for the V(r) characteristics.

Existence of local minimum in the Milky Way

In the analytical solution V(r) (equation (11), the existence of a minimum (r₁ V_min) was predicted for the first time from the functional form of the distance r, and this has been confirmed by the observational data. This minimum was shown to be generated by the increasing/decreasing relationship between the functions of two centripetal forces, owing to the bulge and the disk. In addition to the rotation curve V(r), the equations relating the bulge mass M₀ and the disk mass M_d(r) are given all of the coefficients by two parameters r₁ and V_min, owing to the fact that the minimum is used for fitting equation (11). Among them, the V(r) characteristics are consistent for the whole region of the observed data with high accuracy, although the fitting is performed with only one minimum value. From these points, the minimum value (r₁, V_min) is inferred to be the important parameter that dominates and controls the spiral galaxies from the kinematic point of view.

Quarter power rule of rotation curve

The analytical solution V(r), which consists of two terms, the bulge and the disk, is proportional to r^1/4 of the disk (predicts the existence of the "1/4 power law") when the bulge term is removed in the analysis. Although the spiral galaxies are considered to have (or need) the bulge from Hubble's shape classification, the discovery of the spiral force infers that they can be maintained without the existence of the bulge. Then, in order to confirm the existence of the 1/4 power law, it is taken the observational data of Sc galaxies described in the paper [9]. by Vera Rubin et al. and verified it. From the results of this verification, Sc galaxies have negligible bulges in many cases, and it is quite possible that the bulge did not exist in the early stage of galaxy formation.

Maintenance function and universal characteristic value of spiral exponent

The spiral exponent |α| is a new parameter introduced for the first time in the new model, and is expressed as the function of two variables, the aperture ratio α and the pitch angle ∆ф, which indicate the spiral shape. In the Milky Way, although there are two pairs of the point-symmetric spiral arms and the values of α and ∆ф are different for each pair, it was confirmed that the exponent |α| is maintained at a constant value of 0.5. Furthermore, as shown in Section 5.7 above, the existence of the 1/4 power law, which was verified for the Sc galaxies, is already the precondition for the exponent |α| to have the value of 0.5. From this, the value of 0.5 is inferred to be a universal characteristic value for maintaining the stability of the spiral galaxies.

Fluctuations in Rotation Curves

It has been known that there are fluctuations in the V(r) characteristics based on observed data. However, since the cause of the fluctuations cannot be elucidated, in most cases they have been regarded as errors and treated as average values. In this
context, the paper by Vera Rubin et al [14]. points out that the fluctuation is not errors but secondary velocity fluctuations, based on individual measured value data. However, they dose not indicate the cause of the occurrence.

In the verification of the analytical solution V(r)_b by the new model, it was found that the fluctuation characteristics are an inherent property of the spiral arms and not an error. Therefore, a new local fluctuation model was proposed to explain the cause of this characteristics. Future analysis of the fluctuation characteristics based on this model may provide new insights into the disk section including the spiral arms. In addition, the evaluation of measurement error will be improved by isolating the fluctuation characteristics from the observed data.

Hypothesis on evolution of spiral galaxies

By focusing on the rigid motions of the bulge and the outer disk region (r₁ ≤ r ≤ r₃), and the galaxies without the bulge, as one hypothesis, the flow of structural changes in the formation process of the galaxies is considered to exist. This flow is inferred to be an essential characteristic of the stellar population to obtain more stable rigid body motion (from a two-dimensional spiral shape to a more stable three-dimensional bulge structure). In the early stage of galaxy formation, the galaxy starts from only a disk (no or negligible bulge) as seen in Sc galaxies, followed by the formation of a bulge (the Milky Way), and finally evolves into the old (long-term) stable elliptical galaxy without the disk. However, the mechanism of how the bulge and the elliptical galaxies have been able to achieve more stable rigid body motions in the three-dimensional structure, is still a mystery. Based on the results of the analysis with the new model, the observational data of the inner region (r₀ ≤ r ≤ r₁) (the region between the outer region and the bulge) in the Milky Way is considered to be the key for the elucidation of the mechanism.

Similar to the spiral force in the spiral galaxies, the mechanisms that form new rigid body motions are expected to exist in the bulge and the elliptical galaxies.

Acknowledgment

In this study, the new model was verified, but some observational data were required to analyze and evaluate the process. As a result of the searching for previously reported papers, the following papers (references) were found to provide the important analog data.

1. Observational data showing the spiral shape ( the aperture ratio , the pitch ∆ф) of the Milky Way [19]. Figure 7 in the study by H. Nakanishi and Y. Sobue (2014).
2. Observational data of the rotation curve V(r) of the Milky Way [3]. Figure 3 in the study by J. E. Gunn, G. R. Knapp, & S. D. Tremaine (1979).
3. Observational data for the rotation curve V(r) for 21 Sc galaxies [9]. Figure 7. in the study by V. C. Rubin, W. K. Ford, N. Jr. & Thonnard (1980).
4. Observational data for the rotation curve V(r) for NGC 2998 [14]. Figure 2 and Figure 4. in the study by V. C. Rubin, W. K. Ford, N. Jr. & Thonnard (1978).

I would like to thank the authors for allowing me to cite these data, which enabled me to substantially complete this study. I believe that more observational data acquisition is needed in the future to deepen our understanding of the spiral galaxies such as the Milky Way.

References

1. F. Zwicky (1933) THE REDSHIFT OF EXTRAGALACTIC NEBULAE, Helv. Phys. Acta 6: 110-127.
2. G. Bertone., D. Hooper (2016) A History of Dark Matter, FERMILAB-PUB-16-157-A, III: 11-15.
3. J. E. Gunn., G. R. Knapp., S. D. Tremaine: The Global Properties of The Galaxy.  II. The Galactic Rotation Parameters From 21-CM H₁ Observations. AJ 84: 1181.
4. F. J. Kerr., D. Lynden-Bell (1986) Review of galactic constants. MNRAS 221: 1023-1038.
5. M. J. Reid., T. Dame (2016) On the Rotation Speed of the Milky Way Determined from H₁ Emission. ApJ 832: 159.
6. Y. Sofue (2014) Rotation Curve of the Milky Way and the Dark Matter Density. Galaxies 8: 37.
7. Y. Sofue (2014) Rotation and Mass in the Milky Way and Spiral Galaxies. PASJ 00: 1-34.
8. Y. Sofue (2017) Rotation and mass in the Milky Way and spiral galaxies. PASJ 69: 1-35.
9. V. C. Rubin., W. K. Ford, Jr., N. Thonnard (1980) Rotational Properties of 21 Sc Galaxies with a Large Range of Luminosities and RADII, From NGC 4605 (R = 4 kpc) TO UGC 2885 (R = 122 kpc). ApJ, 238: 471-487.
10. N. Sugiyama (2019) A Major Development in Cosmology (<Special Issue> "The Heisei Era"). JPSJ 74: 362-363.
11. N. Sugiyama (2015) General Relativistic Cosmology (<Special Issue> Continuing Development of General Relativity-The Beginnings, Developments and "Hope" of Space-Time Theory). JPSJ 70: 111-118.
12. A. Nusser (2002) Modified Newtonian dynamics of large-scale structure, MNRAS 331: 909-916.
13. S. M. Kent (1986) Dark Matter in Spiral Galaxies. I. Galaxies with Optical Rotation Curves, AJ 91: 1301-1327.
14. V. C. Rubin., W. K. Ford, Jr., N. Thonnard (1978) Extended rotation curves of high-luminosity spiral galaxies. IV. Systematic dynamical properties, Sa -> Sc.  ApJ 225: L107-L111.
15. M. Miyamoto., R. Nagai (1975) Three-dimensional models for the distribution of mass in galaxies. PASJ 27: 533.
16. R. Reyes., R. Mandelbaum., J. E. Gunn (2012) Optical-to-virial velocity ratios of local disc galaxies from combined kinematics and galaxy–galaxy lensing. MNRAS 425: 2610-2640.
17. G. de Vaucouleurs (1953) On the Distribution of Mass and Luminosity in Elliptical Galaxies. MNRAS 113: 134-161.
18. K. Miuchi., K. Hamaguchi (2020) Current Status of Direct Searches for Dark Matter in the Universe. JPSJ 75: 68-76.
19. H. Nakanishi., Y. Sofue (2014) Three-Dimensional Distribution of the ISM in the Milky Way Galaxy: III. The Total Neutral Gas Disk, PASJ 00: 1-14.
20. J. P. Vallee (2015) Kinematic structure of the Milky Way galaxy, near the spiral arm tangents. MNRAS 450: 4277-4284.
21. Y. Sofue (1997) Nuclear-to-Outer Rotation Curves of Galaxies in the CO and Hi Lines. PASJ 49: 17-46.
22. M. J. Reid., K. M. Menten., A. Brunthaler (2014) Trigonometric Parallaxes of High Mass Star Forming Regions: The Structure and Kinematics of the Milky Way. ApJ 783: 13.