The Allais effect[1] is the alleged anomalous behavior of pendulums which is sometimes purportedly observed during a
solar eclipse. The ef fect was first reported as an anomalous precession of the plane of oscillation of a Foucault pendulum during the solar eclipse of June 30, 1954 by Maurice Allais, a French polymath who went on to win the Nobel Prize in Economics. Allais reported another observation of the effect during the solar eclipse of October 2, 1959 using the paraconical pendulum he invented. This study earned him the 1959 Galabert Prize of the French Astronautical Society and made him a laureate of the U.S. Gravity Research Foundation for his 1959 memoir on gravity.
Gravitomagnetic tensor[4] generates the extra force needed to explain the anomalous behavior of pendulums observed during a solar eclipse.
Gravitomagnetic Tensor; Gravitational Magnetic Field; Energy Momentum 1-Form; Allais Effect; Maxwell`S Equations; Foucault Pendulum; Anomalous Behavior; Solar Eclipse; General Relativity; Special Relativity
Maurice Allais emphasized the ”dynamic character” of the effects he observed.The observed effects are only seen when the pendulum is moving. They are not con- nected with the intensity of weight (gravimetry), but with the variation of weight (or of inertia) in the space swept by the pendulum. Actually, while the move- ment of the plane of oscillation of the pendulum is inexplicable by the theory of gravitation, the deviations from the vertical are explained perfectly by that theory.
Romanian physicist Gheorghe Jeverdan observed the Allais effect and the so- called Jeverdan-Rusu-Antonescu effect or Jeverdan effect (i.e. the change in the oscillation period of a pendulum during an eclipse) while monitoring a Foucault pendulum during the solar eclipse of February 15, 1961.
Electromagnetic tensor is a 2-form derived from the exterior derivative of a 1-form, similarly Gravitomagnetic tensor[4] can be derived from the exterior derivative of the Energy-momentum 1-form and we obtain the similar Maxwell‘s equations.
Electromagnetic form is a 2-form [2].
F = −Exdt ∧ dx − Eydt ∧ dy − Ezdt ∧ dz + Bxdy ∧ dz + Bydz ∧ dx + Bzdx ∧ dy (1)
Energy-momentum form is a 1-form [2].
p = −Edt + pxdx + pydy + pzdz (2)
Gravitomagnetic form is a 2-form
G = dp = −Exdt ∧ dx − Eydt ∧ dy − Ezdt ∧ dz + Bxdy ∧ dz + Bydz ∧ dx + Bzdx ∧ dy (3)
G01 = −Ex = px,t + E,x (4)
G02 = −Ey = py,t + E,y (5)
G03 = −Ez = pz,t + E,z (6)
G23 = Bx = pz,y − py,z (7)
G31 = By = px,z − pz,x (8)
G12 = Bz = py,x − px,y (9)
dG = ddp = 0 [3], we obtain the similar Maxwell‘s equations
Div B = 0 (10)
Curl E = −B,t (11)
* is the Hodge dual [3].
*G = Bxdt ∧ dx + Bydt ∧ dy + Bzdt ∧ dz + Exdy ∧ dz + Eydz ∧ dx + Ezdx ∧ dy (12)
d*G = 4π*J [3], we obtain the last 2 equations with ρ, the mass density
Div E = 4πρ (13)
Curl B = E,t + 4πJ (14)
where Eρσ is the stress-energy tensor of the field.
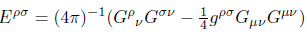(15)
A simple gravity pendulum is an idealized mathematical model of a real pendulum[5], in this model there is no frictional energy loss and motion occurs only in two dimensions, r and θ, m is the mass, g is the magnitude of the gravitational field, l is the length of the rod or cord, θ is the angle from the vertical to the pendulum, and Ft is the tension force.
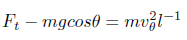(16)
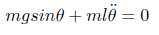(17)
θ<< 1, the approximate period of the motion is then T = 2π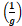
1/2 (18)
Gravitational potential energy is converted into kinetic energy
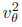= 2gl (cosθ − cosθ0) (19)
During a solar eclipse the flux of electromagnetic energy is distorted, taking into account the mass-energy equivalence, the distorted mass energy flux generates a gravitational magnetic field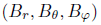 
that interacts on the pendulum.
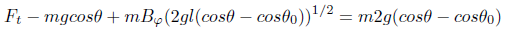(20)
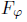= mBr(2gl(cosθ − cosθ0))1/2 (21)
Comparing equations (16) and (20) is evident that the period of the motion is changed and in equation (21) 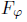is perpendicular to the plane of oscillation causing its anomalous precession.
Gravitomagnetic tensor has been derived from the Energy-momentum and we have obtained the similar Maxwell‘s equations, when a charged particle is mov- ing it generates a magnetic field that interacts with charged particles in motion, similarly when a particle is moving it generates a gravitational magnetic field that interacts with other particles in motion.
The change in the period of the motion and the anomalous precession of the plane of oscillation have been successfully explained by the Gravitomagnetic tensor.
Galaxies in our universe are rotating with such speed that the gravity generated by their observable matter could not possibly hold them together. Gravitomag- netic tensor and the interaction due to the torsion tensor explain dark matter, the shape of galaxies and their distribution in the universe.
Gravitational magnetic force explains other anomalies such as that of the Pio- neer spacecraft and its acceleration when moving away from the Sun.
- Allais effect (2021) wikipedia.org.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University Press 91.
- J.A. Wheeler., C. Misner., K.S. Thorne (2017) Gravitation. Princeton University Press 113.
- Delso J (2022) On Gravitomagnetic Tensor Derived from Energy Momentum 1-Form in a Riemann-Cartan Space with a Metric Connection. OSP Journal of Physics and Astronomy 3: JPA-3-126.
- Pendulum (mechanics) (2022) wikipedia.org.
